lintcode_114_不同的路径

不同的路径

 

• 描述
• 笔记
• 数据
• 评测

有一个机器人的位于一个 m × n 个网格左上角。

机器人每一时刻只能向下或者向右移动一步。机器人试图达到网格的右下角。

问有多少条不同的路径？

注意事项

n和m均不超过100

您在真实的面试中是否遇到过这个题？

Yes

哪家公司问你的这个题？ LinkedIn Amazon Airbnb Cryptic Studios Dropbox Epic Systems TinyCo Hedvig Uber Yelp Apple Yahoo Bloomberg Zenefits Twitter Microsoft Google Snapchat Facebook

感谢您的反馈

样例

给出 m = 3 和 n = 3, 返回 6.
给出 m = 4 和 n = 5, 返回 35.

标签

动态规划 数组

相关题目

 

 

 

这道题目很有趣，直接用组合秒解。但是我并没有掌握什么方便解组合的函数，数字一大就不行了。

既然用dp来做，那就要用dp思想：分阶段。

我直接想到每一步所能走的最多次数来解，恰好解出来。

思路如下：

          只能向右或向下移动，则最上方一行与最左边一列的值为1，并且当前位置的步数则是上边格子的 步数 与 左边格子的 步数之和。

例1：

 

 

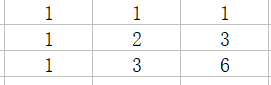答案为6。

 

 

 

class Solution {
public:
    /*
     * @param m: positive integer (1 <= m <= 100)
     * @param n: positive integer (1 <= n <= 100)
     * @return: An integer
     */
     int a[101][101];
    int uniquePaths(int m, int n) {
        // write your code here
        for(int i =0;i<m;i++)
            a[i][0]=1;
        for(int i =0;i<n;i++)
            a[0][i]=1;
        for(int i =1;i<m;i++)
            for(int j=1;j<n;j++)
                a[i][j]=a[i-1][j]+a[i][j-1];
        return a[m-1][n-1];
    }
};