POJ3071(Football)--概率DP
题意:有(1<<n个足球队进行比赛,在经过多轮一对一淘汰赛后决出冠军队伍,问最后哪支队伍能够获胜,即输出获胜概率最大的那支队伍编号。给了你n*n的矩阵,用来表示每支队伍间的各自胜率。输入-1为表示结束
en....网上当然也后不少解题报告,但是很多直接给出状态转移方程和贴出代码,而少了其中重要的推断过程,我觉得不是很好。所以自己给写一个较为详细的过程
首先呢,以n==3为例子,即8支队伍参赛。一种比赛情形是这样的

由图可知,在题中给定n后,需要比赛n轮即可知道冠军队伍是谁,我这里多了个第0轮是为了后面计算需要
其次,对于DP的题目,我们首先要明确状态转移方程代表的含义是什么,我们已知什么,未知什么,怎么去确定合适的方程,这些是很重要的,当然,推出转移方程到后面更难的题目则是更重要的。
既然要求出最终能获胜的队伍,即求出每个队伍的在最后一轮的胜率,最后取一个最大值就ok了。并且,获得冠军的那支队伍既然能够到达最后一轮,那么,它一定经历了所有轮次的比赛,并且都赢了。在这每一轮比赛的胜率,就是子问题了。这是很简单就可以得出的。所以,后一轮的胜率,肯定是由上一轮的胜率决定的。
所以,DP[i][j]可以这么定义,它表示为在第i轮中,第j只队伍的胜率。这也符合求解问题的逻辑,我们已知总共的轮数(n),已知所有队伍的数量(1<<n),要求胜率最大的那支队伍的编号(?) :max(DP[n][?])
DP的含义确定了,那么,状态转移方程怎么来呢??
首先,dp数组的第一维表示的是整个赛事的轮数,所以外面有一层循环,接着,第二维表示每只队伍,所以又一层循环遍历每一只队伍。那么对应的概率到底怎么来呢.....
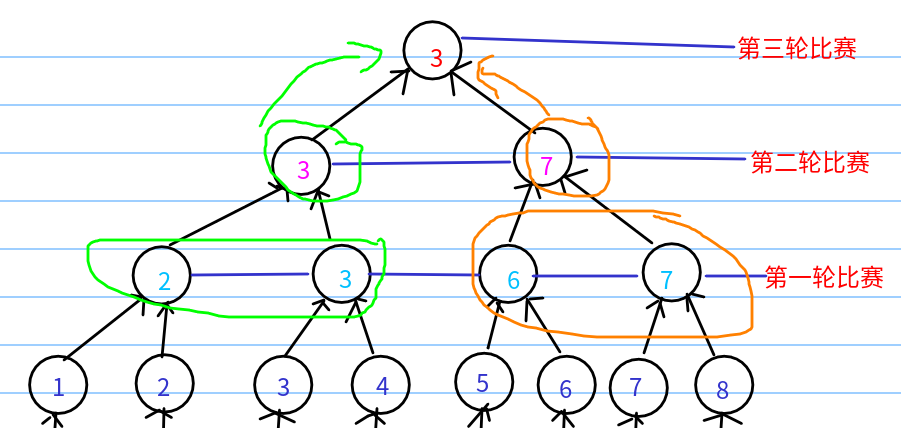
因为对于树中的每个结点代表对应DP[i][j]的概率,即两支队伍某一方击败另一方,并且,这两支队伍在上一轮中都双双各自获胜,我们直接看最后一轮比赛/最上面一个结点,因为,所有底下结点是子问题,性质都一样,所以可以得到部分转移方程:(假设最后一轮是j赢了,此时i==3,概率为DP[i][j])
DP[i][j] = DP[i-1][j] * DP[i-1][k] * ???;
DP[I-1][j]:表示本轮的赢家j在上一轮获胜的概率,上一轮一定是获胜了的再能到这一轮
DP[i-1][k]:表示本轮赢家j遇见的对手k,k在上一轮获胜的概率,k也晋级到了这一轮
???:这个表示什么呢???因为此时DP[i][j]表示这一轮是j获胜的概率,所以j战胜了k,那么胜率是多少呢??
在题中输入的矩阵中第j行k列就是这里的概率
所以完整的状态转移方程:(当前概率+=上一轮二者分别获胜的概率 * 这一轮一方胜另一方的概率)
1 dp[i][j] += dp[i-1][j] * dp[i-1][k] * G[j][k];
别以为到这里就结束了,k 的范围还没确定呢!!
从图中可知,在第二轮中3号结点不会遇见所有的对手,只有可能遇见来自另一边的5,6,7,8的某一个,
而1,2,4是不可能再遇见了(已经淘汰了)。那么,k的编号怎么判断呢??(关键)
假设最后是j和k进行决赛,那么表明j和k一定是在最后一轮相遇了,在倒数第二轮它们不会相遇,因为它们各自再进行半决赛(好像说了句废话,但是....)k的范围就这样确定。
因为到了最后一轮,所以遍历轮数的编号i此时为3,如图中,j为3,最后是k==7与之对决。
它们满足这样了个关系:
3 /(1<<3) == 7/(1<<3) ==>0 && 3 /(1<<2 ) != 7/(1<<2)
公式是这样的
((j / (1<<i)) == (k / (1<<i)) ) && ( j /(1<<(i-1)) != (k / (1<<(i-1))) )
即对于某个j,判断k是否能和j同时成为一个点的左右孩子结点。这个条件就满足了对可能遇见的对手的的选取
这里还是要稍微思考下的。

1 #include<iostream>
2 #include<cstdio>
3 #include<algorithm>
4 #include<cstring>
5 using namespace std;
6 const int maxn = 130;
7 int n;//总过(1<<n)个队伍
8 double G[maxn][maxn];//存放各个队伍间的胜率关系 G[i][j]即队伍i击败队伍j的概率
9 double dp[maxn][maxn];//dp[i][j]表示在第i轮第j只球队获胜的概率
10
11 void DP()
12 {
13 for(int i = 0;i < (1<<n);i++)//算出每个队伍第0场的胜率,都为1.0
14 {
15 dp[0][i] = 1.0;
16 }
17 for(int i = 1;i <= n;i++)//决出冠军最多的轮数,一棵二叉树的深度-1
18 {
19 for(int j = 0; j < (1<<n);j++)//遍历每个队伍,计算出当前轮次的胜率
20 {
21 dp[i][j]= 0.0;//注意别忘了这个init
22 for(int k = 0; k < (1<<n);k++)//遍历可能交手的队伍
23 {
24 if(j == k)
25 {
26 continue;//自己与自己不交手
27 }
28 //关键部分,j和k在决赛轮相遇,而在决赛轮之前它们是不会遇见的,即j和k是来自两个不同的小组的队伍
29 if(((j / (1<<i)) == (k / (1<<i)) ) && ( j /(1<<(i-1)) != (k / (1<<(i-1))) ) )
30 {
31 dp[i][j] += dp[i-1][j] * dp[i-1][k] * G[j][k];
32 // j上一轮获胜的概率 * k上一轮获胜的概率 * 最后一轮j战胜k的概率
33 }
34 }
35 }
36 }
37 }
38
39 int main()
40 {
41 while((scanf("%d",&n)&& n != -1))
42 {
43 for(int i =0 ;i< (1<<n);i++)
44 {
45 for(int j = 0;j < (1<<n);j++)
46 {
47 scanf("%lf",&G[i][j]);
48 }
49 }
50 DP();
51 int ans = 0;//保存胜率最大的队伍编号
52 for(int j = 1 ;j < (1<<n);j++)//遍历每一只队伍
53 {
54 if(dp[n][ans] < dp[n][j])//更新胜率大的队伍
55 {
56 ans = j;
57 }
58 }
59 cout<<ans+1<<endl;
60 }
61 return 0;
62 }




