洛谷P3372--线段树代码模板1

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.求出某区间每一个数的和

输入格式

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式

输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入 #1 
5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4
输出 #1 
11
8
20

说明/提示

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^，保证在int64/long long数据范围内）

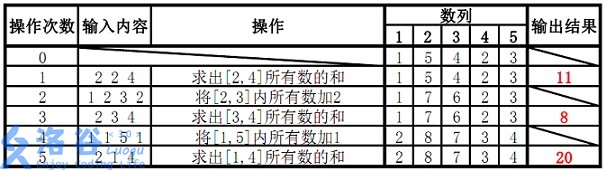
样例说明：

  1 #include<iostream>
  2 #include<stdio.h>
  3 #include<cstring>
  4 #include<cmath>
  5 #include<vector>
  6 #include<stack>
  7 #include<map>
  8 #include<set>
  9 #include<list>
 10 #include<queue>
 11 #include<string>
 12 #include<algorithm>
 13 #include<iomanip>
 14 using namespace std;
 15 const int maxn = 100010;
 16 int arr[maxn +5];
 17 struct node
 18 {
 19     /* data */
 20     long long  value;//该结点维护的值
 21     int left;
 22     int right;
 23     long long add;//lazy 每个区间的增量
 24 }tree[maxn* 4 + 5];
 25 
 26 
 27 inline void PushUp(int root)
 28 {
 29     tree[root].value = tree[root <<1].value + tree[root<<1|1].value;
 30 }
 31 
 32 void Build(int root,int x,int y)
 33 {
 34     tree[root].left = x;
 35     tree[root].right = y;
 36     if(x == y)
 37     {
 38         tree[root].value = arr[x];
 39         return ;
 40     }
 41     int mid = (x + y) >> 1;
 42     Build(root<<1,      x,mid);
 43     Build(root<<1|1,mid+1,y);
 44     PushUp(root);
 45 }
 46 
 47 void Spread(int root)//懒标记
 48 {
 49     if(tree[root].add)//如果树根结点的懒标记不为0 ，修改左右儿子的值
 50     {
 51         tree[root<<1].value   += tree[root].add * (tree[root<<1].right   - tree[root<<1].left   +1);
 52         tree[root<<1|1].value += tree[root].add * (tree[root<<1|1].right - tree[root<<1|1].left +1);
 53         //左右儿子的值增加为父亲结点的增量乘以自己各区间的长度
 54         tree[root<<1].add   += tree[root].add;
 55         tree[root<<1|1].add += tree[root].add;
 56         tree[root].add = 0;//父亲结点增量变为0;
 57     }
 58 }
 59 void Change(int root,int x,int y,int z)//给根结点为root 区间为(x,y)的每个值加上z
 60 {
 61     if( x <= tree[root].left && y  >= tree[root].right)//区间被完全覆盖
 62     {
 63         tree[root].value += (long long )z * (tree[root].right - tree[root].left + 1);
 64         tree[root].add   += z;
 65         return ;
 66     }
 67     Spread(root);//如果没有发现区间被覆盖，即需要继续向下找，并把懒标记下放
 68     int mid = (tree[root].right + tree[root].left) >> 1;
 69     if( x <= mid)//要修还区间覆盖了左儿子，修改
 70     {   
 71         Change(root<<1,x,y,z);
 72     }
 73     if( y > mid)//右儿子同理
 74     {
 75         Change(root<<1|1,x,y,z);
 76     }
 77     PushUp(root);
 78 }
 79 
 80 long long Query(int root,int x,int y)//对区间(x,y)的查询操作
 81 {
 82     long long ans = 0;
 83     if( x <= tree[root].left && y >= tree[root].right )//查询区间被根结点所对应区间覆盖
 84     {
 85         return tree[root].value;
 86     }
 87     Spread(root);//下传懒标记
 88     int mid = (tree[root].left + tree[root].right) >> 1;
 89     if ( x <= mid)
 90     {
 91         ans += Query(root<<1,x,y);
 92     }
 93     if( y > mid)
 94     {
 95         ans += Query(root<<1|1,x,y);
 96     }
 97     return ans;
 98 }
 99 
100 int main()
101 {
102     int n,m;
103     scanf("%d%d",&n,&m);
104         for(int i = 1; i<= n;i++)
105         {
106             scanf("%d",&arr[i]);
107         }
108         Build(1,1,n);
109         for(int i = 0 ;i < m;i++)
110         {
111             int flag;
112             int x,y,k;
113             cin>>flag;
114             if(flag == 1)
115             {
116                 scanf("%d%d%d",&x,&y,&k);
117                 Change(1,x,y,k);
118             }
119             else
120             {
121                 scanf("%d%d",&x,&y);
122                 cout<<Query(1,x,y)<<endl;
123             }
124         }
125     return 0;
126 }

 

posted @ 2019-07-31 22:55  回忆酿的甜  阅读(522)  评论(0)  编辑  收藏  举报
Live2D