POJ3368(Frequent values)--线段树

题目在这里

3368

Accepted

7312K

1829MS

C++

6936B

题意为给你一组数据，再给定一组区间，问你这个区间内出现次数最多的元素的次数是多少。

我还记得这题是学校校赛基础的题目，当时懵懵懂懂的用分治交了6次TLE。知道了线段树之后才后悔每更早的认识她。

一段区间内的多次出现的数的次数，在线段树查询中有以下几种情况

1.次数最多的都集中在某一结点的左区间内

2.次数最多的都集中在某一结点的有区间内

3.次数最多的在左右两边都有，这时maxCount ==左右两边的maxCount之和

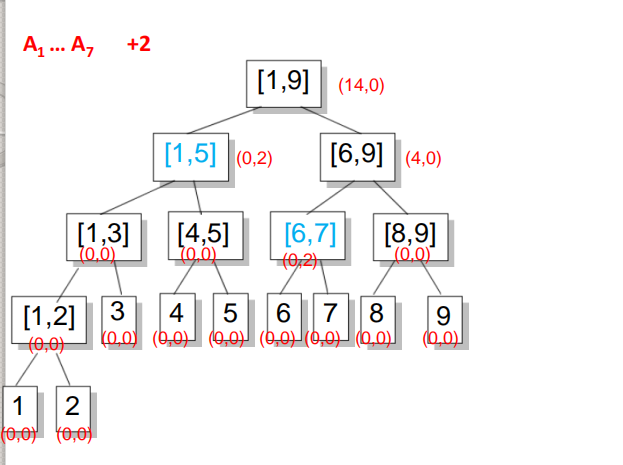
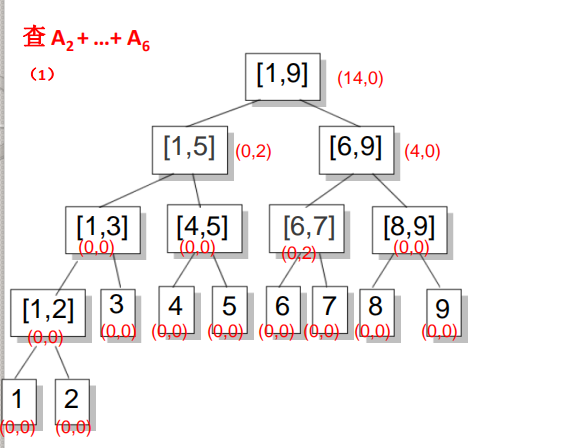
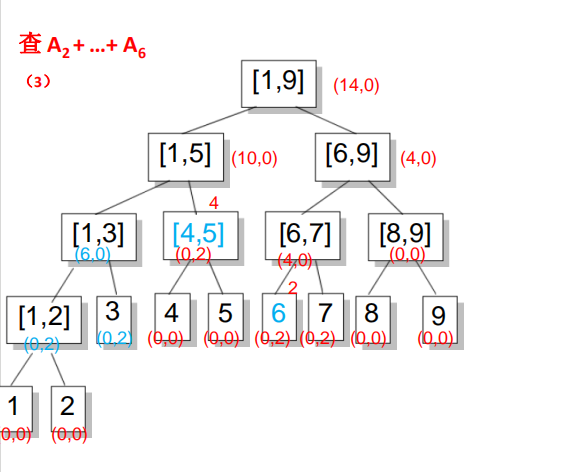
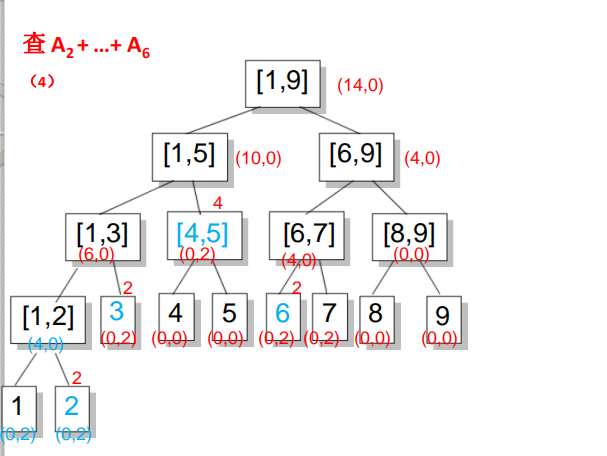
在增加时，如果要加的区间正好覆盖一个节点，则增加其节点的Inc值，不再往下走，否则要更新nSum(加上本次增量),再将增量往下传。这样更新的复杂度就是O(log(n))在查询时，如果待查区间不是正好覆盖一个节点，就将节点的Inc往下带，然后将Inc代表的所有增量累加到nSum上后将Inc清0，接下来再往下查询。

 

 

/*************************************************************************
    > File Name: poj3368rmq.cpp
    > Author: YeGuoSheng
    > Description:  
    > Created Time: 2019年07月11日 星期四 15时34分56秒
 ************************************************************************/

#include<iostream>
#include<stdio.h>
#include<cstring>
#include<cmath>
#include<vector>
#include<stack>
#include<map>
#include<set>
#include<list>
#include<queue>
#include<string>
#include<algorithm>
#include<iomanip>
using namespace std;

template <typename T>
struct node
{
    int l;
    int r;//左右区间端点
    T value;
    T add;
    int lCount;//元素在左边的计数
    int rCount;//元素在右边的计数
    int maxCount;//总计出现的次数
    int Len()const;
    int Mid()const;
};

template <typename T>
int node<T>::Mid()const
{
    return (r  + l )/ 2;
}

template<typename T>
int node<T>::Len()const
{
    return (r - l ) +1;
}

template<typename T>
class IntervalTree
{
protected:
    int n;
    node<T>*tree;
public:
    IntervalTree(int n);
    ~IntervalTree();
    void BuildTree(int v,int l,int r);
    void Add(int v,int l,int r,T m);
    T Query(int v,int l,int r);
    void Insert(int v,int i,T value);
    void BuildCount(int v,int l,int r);
    int FindIndexInTree(int v,int y);//在数组下标为u的在树中的下标
};

template<typename T>
IntervalTree<T>::IntervalTree(int n)
{
    this->n = n;
    tree = new node<T>[4*n];
}

template<typename T>
IntervalTree<T>::~IntervalTree()
{
    delete []tree;
}

template<typename T>
void IntervalTree<T>::BuildTree(int v ,int l,int r)
{
    tree[v].l =l;
    tree[v].r = r;
    tree[v].add = 0;
    tree[v].value = 0;
    if(l == r)//相等
    {
        tree[v].lCount =tree[v].rCount = tree[v].maxCount = 1;
        return ;
    }
    int mid =(l + r) /2;//二分
    BuildTree(v* 2+1,l,mid);
    BuildTree(v*2+2,mid+1,r);
    tree[v].value = tree[2*v+1].value + tree[2*v+2].value;
}


template<typename T>
int IntervalTree<T>::FindIndexInTree(int v,int u)
{
    if( tree[v].l == u && tree[v].r == u)
    {
        return v;
    }
    else
    {
        int mid = (tree[v].l + tree[v].r) / 2;
        if(u <= mid)
        {
            FindIndexInTree(v * 2+1,u);
        }
        else
        {
            FindIndexInTree(v * 2+2,u);
        }
    }
}

template<typename T>
void IntervalTree<T>::BuildCount(int v,int l ,int r)
{
    tree[v].l = l;
    tree[v].r = r;
    if(l == r)
    {
        tree[v].lCount = tree[v].rCount =tree[v].maxCount = 1; 
        return ;
    }
    int mid  = (l + r )/ 2;
    BuildCount(2* v+ 1,l,mid);
    BuildCount(2*v +2,mid+1,r);
    int repeat = 0;
    int leftIndex = FindIndexInTree(v,tree[2*v+1].r);
    int rightIndex = FindIndexInTree(v,tree[2*v+2].l);
    if(tree[leftIndex].value == tree[rightIndex].value)
    {
        repeat = tree[2 * v +1].rCount + tree[2*v +2].lCount;
    }
    else
    {
        repeat = 0;
    }
    tree[v].maxCount = max( repeat,max( tree[2*v+1].maxCount, tree[2*v+2].maxCount) );
    tree[v].lCount = tree[2*v+1].lCount;
    if(tree[2*v + 1].lCount == mid - l + 1 && tree[leftIndex].value==tree[rightIndex].value)
    {
        tree[v].lCount += tree[2*v +2].lCount;
    }
    if(tree[2*v + 2].rCount == r- mid  && tree[rightIndex].value==tree[leftIndex].value)
    {
        tree[v].rCount += tree[2*v +1].rCount;
    }
}
template<typename T>
void IntervalTree<T>::Add(int v,int l,int r,T m)//区间的更新操作
{
    if(tree[v].l == l && tree[v].r == r)
    {
        tree[v].add +=m;
        return ;
    }
    tree[v].value += m * (r- l +1);
    int mid = (tree[v].l  + tree[v].r) /2;
    if( r<= mid)
    {
        Add(v *2 +1,l,r,m);
    }
    else
    {
        if(l > mid)
        {
            Add(v *2 +2,l,r,m);
        }
        else
        {
            Add(v *2 +1,l,mid,m);
            Add(v*2+2,mid+1,r,m);
        }
        
    }
    
}
template<typename T>
T IntervalTree<T>::Query(int v,int l,int r)//对根结点为v，查询区间l 到 r
{
    if(tree[v].l == l && tree[v].r == r)
    {
        return tree[v].value +(tree[v].r - tree[v].l +1) * tree[v].add;
    }
    if(tree[v].add != 0)
    {
        tree[v].value += (tree[v].r - tree[v].l +1) * tree[v].add;
        Add( v * 2 +1,tree[v].l,tree[v].Mid(),tree[v].add);
        Add( v * 2 +2,tree[v].Mid()+1,tree[v].r,tree[v].add);
        tree[v].add = 0;
    }
    int mid = tree[v].Mid();
    if( r <= mid)
    {
        return     Query(v  * 2 +1,l,r);
    }
    else
    {
        if( l > mid)
        {
            return Query(v * 2+ 2,l ,r);
        }
        else
        {
            return Query(v * 2+1,l,mid) + Query(v* 2+2,mid+1,r);
        }        
    }
}

template<typename T>
void IntervalTree<T>::Insert(int r,int i,T value)
{
    if(tree[r].l == i && tree[r].r == i)
    {
        tree[r].value= value;
        return ;
    }
    tree[r].value += value;
    if(i <= tree[r].Mid())
    {
        Insert(2*r+1,i,value);
    }
    else
    {
        Insert(2 * r+ 2,i,value);
    }
}

int main()
{
    int n = 0;
    while(cin>>n && n > 0)
    {
        IntervalTree<int> it(n);
        it.BuildTree(0,0,n-1);
        int q = 0;
        scanf("%d",&q);
        for(int i = 0; i< n;i++)
        {
            int num = 0;
            scanf("%d",&num);
            it.Insert(0,i,num);
        }
        it.BuildCount(0,0,n-1);
        for(int i =0 ;i < q;i++)
        {
            int x,y;
            cin>>x>>y;
            cout<<it.Query(0,x-1,y-1)<<endl;
        }
    }
    return 0;
}