Tree Traversals Again
本博客的代码的思想和图片参考:好大学慕课浙江大学陈越老师、何钦铭老师的《数据结构》感谢PTA代码测试工具
Tree Traversals Again
1 Question
An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤30) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to N). Then 2N lines follow, each describes a stack operation in the format: "Push X" where X is the index of the node being pushed onto the stack; or "Pop" meaning to pop one node from the stack.
Output Specification:
For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.
Sample Input:
6Push 1Push 2Push 3PopPopPush 4PopPopPush 5Push 6PopPop
Sample Output:
3 4 2 6 5 1
Solution
2 Algorithm Thoughts
We can get prefer order traversal result by push operation and get inner order traversal result by pop operation. Then we can use those two result to get the post order traversal result.
We know the prefer order traversal result first element is the root element in this binary tree. Then we search this element in inner order result,we use this element as the separation,left elements is the sub left elements,right elements is the sub right elements. Then we recursive call this method, finally we will get the post order result.
2 Data Structure
In this question, we don’t need to construct a binary tree, so we just use three same length integer to store the elements in the tree. We will use followed picture to show the algorithm.
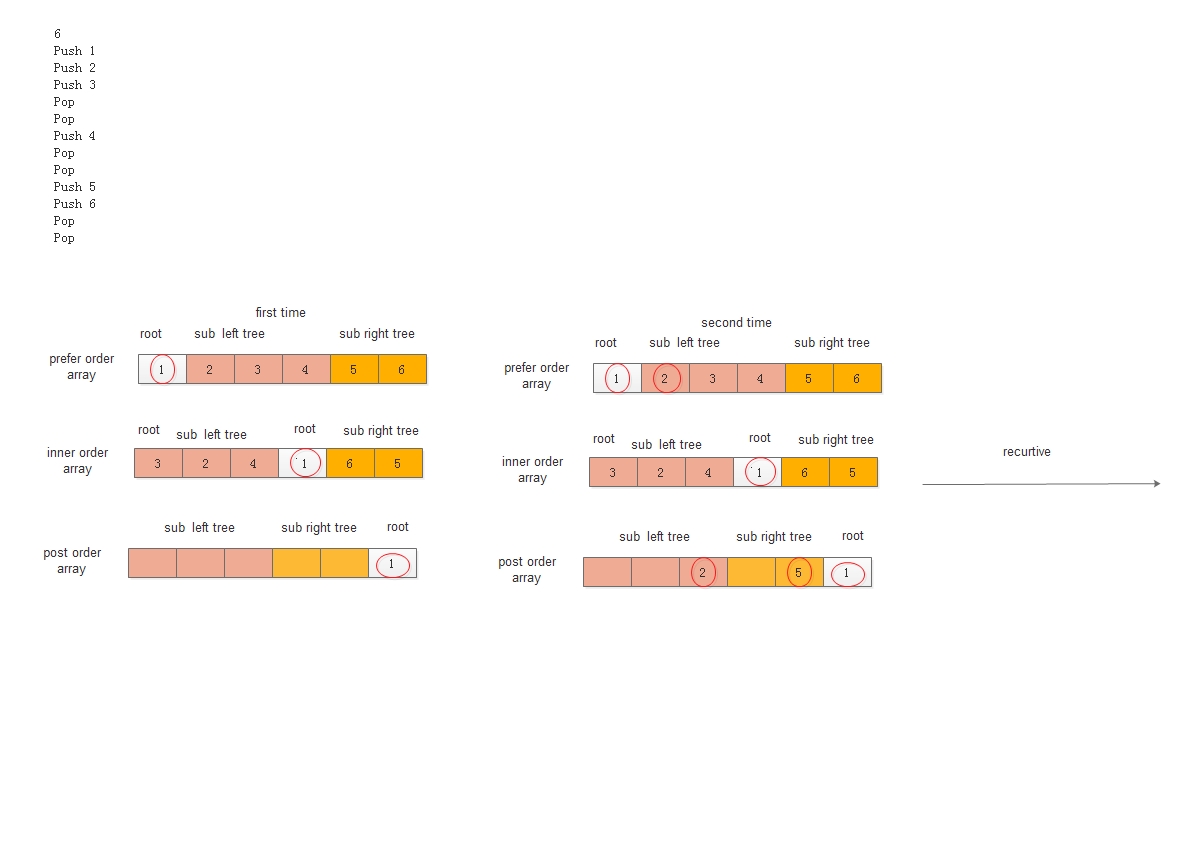
The code is follow:

1 /* 2 * treeTraversalAgain.c 3 * 4 * Created on: 2017年5月11日 5 * Author: ygh 6 */ 7 #include <stdio.h> 8 #include <stdlib.h> 9 #include <string.h> 10 11 /* 12 * Algorithm thoughts: 13 * We can get prefer order traversal result by push operation and get inner order traversal result by pop operation. 14 * Then we can use those two result to get the post order traversal result. 15 We know the prefer order traversal result first element is the root element in this binary tree. 16 Then we search this element in inner order result,we use this element as the separation, 17 left elements is the sub left elements,right elements is the sub right elements. 18 Then we recursive call this method, finally we will get the post order result. 19 */ 20 21 /*===============define a data structure of a stack and some operation======================*/ 22 typedef int elementType; 23 typedef struct node *pStack; 24 typedef struct node { 25 elementType element; 26 struct node * next; 27 }; 28 29 pStack createEmptyStack() { 30 pStack stack = (pStack) malloc(sizeof(struct node)); 31 stack->next = NULL; 32 return stack; 33 } 34 35 int isStackEmpty(pStack stack) { 36 return (stack->next == NULL); 37 } 38 39 void push(pStack stack, elementType elemet) { 40 pStack node = (pStack) malloc(sizeof(struct node)); 41 node->element = elemet; 42 node->next = stack->next; 43 stack->next = node; 44 } 45 46 elementType pop(pStack stack) { 47 if (isStackEmpty(stack)) { 48 printf("the stack is empty"); 49 return -1; 50 } else { 51 pStack node = stack->next; 52 elementType element = node->element; 53 stack->next = node->next; 54 free(node); 55 return element; 56 } 57 58 } 59 60 /* 61 * A method to implement transfer prefer order result and inner order result 62 * into post order result. We use the integer array to store the elements 63 * @param preL The tree or sub tree start index in prefer order result array 64 * @param inL The tree or sub tree start index in the inner order result array 65 * @param postL The tree or sub tree start index in the post order result array 66 * @param n The total nodes in this tree 67 * @param pre The integer array to store the prefer order result 68 * @param in The integer array to store the inner order result 69 * @param post The integer array to store the post order result 70 */ 71 void solve(int preL, int inL, int postL, int n, int *pre, int *in, int *post) { 72 int root, i, leftLength, rightLength; 73 if (n == 0) { 74 return; 75 } 76 77 if (n == 1) { 78 post[postL] = pre[preL]; 79 return; 80 } 81 82 root = pre[preL]; 83 post[postL + n - 1] = root; 84 85 for (i = 0; i < n; i++) { 86 if (in[inL + i] == root) { 87 break; 88 } 89 } 90 leftLength = i; 91 rightLength = n - i - 1; 92 solve(preL + 1, inL, postL, leftLength, pre, in, post); 93 solve(preL + leftLength + 1, inL + leftLength + 1, postL + leftLength, 94 rightLength, pre, in, post); 95 96 } 97 98 /* 99 * A method to get input data 100 * @param n The total nodes of the tree 101 * @param pre A integer array to store the prefer order data,it is null for first. 102 * @param pre A integer array to store the inner order data,it is null for first. 103 */ 104 void getInputData(int n, int *pre, int *in) { 105 int i, data, p = 0, q = 0; 106 char str[3]; 107 pStack stack = createEmptyStack(); 108 for (i = 0; i < 2 * n; i++) { 109 scanf("%s", str); 110 if (strcmp(str, "Push") == 0) { 111 scanf("%d", &data); 112 push(stack, data); 113 pre[p] = data; 114 p++; 115 } 116 117 if (strcmp(str, "Pop") == 0) { 118 data = pop(stack); 119 in[q] = data; 120 q++; 121 } 122 } 123 124 } 125 126 /* 127 * Print a array 128 */ 129 void printArray(int n, int *array) { 130 int i; 131 for (i = 0; i < n; i++) { 132 if (i == n - 1) { 133 printf("%d", array[i]); 134 } else { 135 printf("%d ", array[i]); 136 } 137 } 138 } 139 140 /* 141 * Just a execute method 142 */ 143 int main() { 144 int n; 145 scanf("%d", &n); 146 int pre[n]; 147 int in[n]; 148 int post[n]; 149 getInputData(n, pre, in); 150 solve(0, 0, 0, n, pre, in, post); 151 printArray(n, post); 152 return 0; 153 }
The code test result






 浙公网安备 33010602011771号
浙公网安备 33010602011771号