B树 B+树 红黑树

B-Tree（B树）

具体讲解之前，有一点，再次强调下：B-树，即为B树。因为B树的原英文名称为B-tree，而国内很多人喜欢把B-tree译作B-树，其实，这是个非常不好的直译，很容易让人产生误解。如人们可能会以为B-树是一种树，而B树又是一种树。而事实上是，B-tree就是指的B树。特此说明。

m阶B树的M阶指的是所有结点中的子结点个数的最大值。

一个m阶B树是一棵空树，或者是满足以下条件的树:

（1）结点最多有m个分支。

（2）根结点最少有两个分支，非根非叶结点至少有ceil(m/2)个分支。

（3）结点内关键字递增排序。

（4）一个结点有n-1个关键字，则该结点有n个分支，将关键字一一隔开。

（5）结点中任何一个关键字，其左边分支上的结点值都小于这个关键字，右边分支的结点值都大于这个关键字。

（6）叶子结点处于同一层。

如图5阶B树满足：

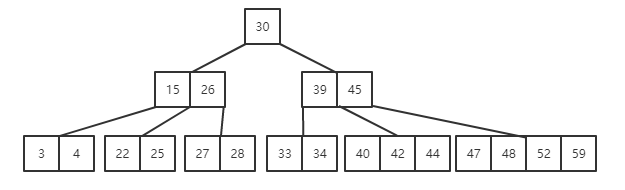
（1）结点最多有5个分支（叶子结点）。

（2）根结点最少有两个分支，非根非叶结点至少有3个分支。

（3）结点内关键字递增排序。

（4）一个结点有2个关键字，则该结点有2+1个分支，将关键字一一隔开。

（5）结点中任何一个关键字，其左边分支上的结点值都小于这个关键字，右边分支的结点值都大于这个关键字。

（6）叶子结点处于同一层。

B树插入操作

由上可知，m阶B树，非根非叶结点至少有ceil(m/2)个分支，最多由m个分支，则结点关键字个数的范围为ceil(m/2)-1 ~ m-1。

B树结点的插入是待插入结点的值与B树结点依次比较的过程，从根结点开始，若小于当前结点的值，则递归与结点的左子树进行比较，若大于则与右子树进行比较。由此可见，B树结点的插入总是落在叶子结点上，在插入过程中可能会破坏B树的特征，如新关键字的插入使得结点中关键字的个数超过规定个数，则要进行结点拆分。

我们以关键字序列{1,2,6,7,11,4,8,13,10,5,17,9,16,20,3,12,14,18,19,15}创建一个5阶B树。

（1）确定结点关键字个数范围，由于创建的是5阶B树，因此关键字的个数范围为2~4。

（2）根结点最多可以容纳4个关键字，依次插入关键字1、2、6、7

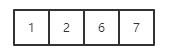
（3）插入关键字11，发现此时结点中关键字的个数变为5，超出范围，需要拆分，去关键字数组中的中间位置，也就是k[3]=6，作为一个独立的结点，即新的根结点，将关键字6左、右关键字分别做成两个结点，作为新根结点的两个分支（图左为拆分前，图右为拆分后）

（4）新关键字总是插在叶子结点上，插入关键字4、8、13

（5）关键字10需要插入在关键字8和11之间，此时又会出现关键字个数超出范围的情况，因此需要拆分。拆分时需要将关键字10纳入根结点中，并将10左右的关键字做成两个新的结点连在根结点上。

（6）插入关键字5、17、9、16

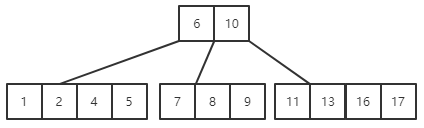
（7）关键字20插入在关键字17以后，此时会造成结点关键字个数超出范围，需要拆分，方法同上

（8）按照上述步骤依次插入关键字3、12、14、18、19

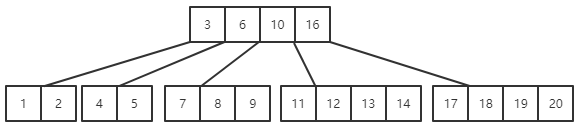
（9）插入最后一个关键字15，15应该插入在14之后，此时会出现关键字个数超出范围的情况，则需要进行拆分，将13并入根结点，13并入根结点之后，又使得根结点的关键字个数超出范围，需要再次进行拆分，将10作为新的根结点，并将10左、右关键字做成两个新结点连接到新根结点的指针上，这种插入一个关键字之后出现多次拆分的情况称为连锁反应

B树删除操作

对于B树关键字的删除，需要找到待删除的关键字，在结点中删除关键字的过程也有可能破坏B树的特性，如旧关键字的删除可能使得结点中关键字的个数少于规定个数，则需要向其兄弟结点借关键字或者和其孩子结点进行关键字的交换，也可能需要进行结点的合并，其中，和当前结点的孩子进行关键字交换的操作可以保证删除操作总是发生在终端结点上。

我们用刚刚生成的B-树作为例子，一次删除8、16、15、4这4个关键字。

（1）删除关键字8、16。关键字8在终端结点上，并且删除后其所在结点中关键字的个数不会少于2，因此可以直接删除。关键字16不在终端结点上，但是可以用17来覆盖16，然后将原来的17删除掉，这就是上面提到的和孩子结点进行关键字交换的操作。这里不能用15和16进行关键字交换，因为这样会导致15所在结点中关键字的个数小于2。

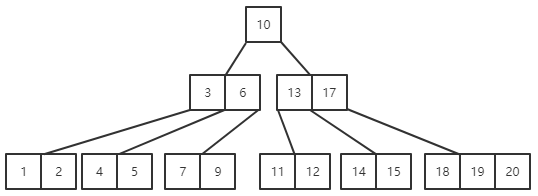
（2）删除关键字15，15虽然也在终端结点上，但是不能直接删除，因为删除后当前结点中关键字的个数小于2。这是需要向其兄弟结点借关键字，显然应该向其右兄弟来借关键字，因为左兄弟的关键字个数已经是下限2.借关键字不能直接将18移到15所在的结点上，因为这样会使得15所在的结点上出现比17大的关键字，所以正确的借法应该是先用17覆盖15，在用18覆盖原来的17，最后删除原来的18。

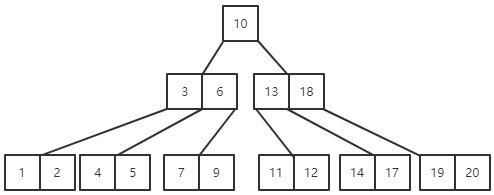
（3）删除关键字4，4在终端结点上，但是此时4所在的结点的关键字个数已经到下限，需要借关键字，不过可以看到其左右兄弟结点已经没有多余的关键字可借。

所以就需要进行关键字的合并。可以先将关键字4删除，然后将关键字5、6、7、9进行合并作为一个结点链接在关键字3右边的指针上，也可以将关键字1、2、3、5合并作为一个结点链接在关键字6左边的指针上.

显然上述两种情况下都不满足B-树的规定，即出现了非根的双分支结点，需要继续进行合并。

有时候删除的结点不在终端结点上，我们首先需要将其转化到终端结点上，然后再按上面的各种情况进行删除。在讲述这种情况下的删除方法之前，要引入一个相邻关键字的概念，对于不在终端结点的关键字a，它的相邻关键字为其左子树中值最大的关键字或者其右子树中值最小的关键字。找a的相邻关键字的方法为：沿着a的左指针来到其子树根结点，然后沿着根结点中最右端的关键字的右指针往下走，用同样的方法一直走到叶结点上，叶结点上的最右端的关键字即为a的相邻关键字（这里找的是a左边的相邻关键字，我们可以用同样的思路找到a右边的相邻关键字）。可以看到下图中a的相邻关键字是d和e，要删除关键字a，可以用d来取代a，然后按照上面的情况删除叶子结点上的d即可。

 

B⁺树

B⁺树是应文件系统所需而出的一种B树的变型树。

一颗m阶的B⁺树和m阶的B树的差异在于：

（1）有n棵子树的结点中含有n个关键字。

（2）所有的叶子结点中包含了全部关键字的信息，及指向含这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。

（3）所有的非终端结点可以看成是索引部分，结点中仅含有其子树（根节点）中最大（或最小）关键字。

如图为一棵3阶的B⁺树，通常在B+树上有两个头指针，一个指向根结点，另一个指向关键字最小的叶子结点。因此，可以对B⁺树进行两种查找算法：一种是从最小关键字起顺序查找，另一种是从根结点开始，进行随即查找。

在B⁺树上进行随机查找、插入和删除过程基本与B树类似。只是在查找时，若非终端结点上的关键字等于给定值，并不终止，而是继续向下直到叶子结点。因此，在B⁺树，不管查找成功与否，每次查找都是走了一条从根到叶子结点的路径。B⁺树查找的分析类似于B树。B⁺树的插入仅在叶子结点上进行，当结点中的关键字个数大于m时要分裂成两个结点，它们所含关键字的个数分别为ceil((m+1)/2)和floor((m+1)/2)。并且，它们的双亲结点中应同时包含这两个结点中的最大关键字。B⁺树的删除也仅在叶子结点进行，当叶子结点中的最大关键字被删除时，其在非终端结点中的值可以作为一个“分界关键字”存在。若因删除而使结点中关键字个数少于ceil(m/2)时，其和兄弟节点的合并过程亦和B树类似。

B⁺树和B树的区别

1.B+树中只有叶子结点会带有指向记录的指针，而B树则所有结点都带有，在内部节点出现的索引项不会再出现在叶子结点中。

2.B+树中所有叶子结点都是通过指针连接在一起的，而B树不会。

 B⁺树相比于B树的查询优势

1.B+树的中间结点不保存数据，所以磁盘页能容纳更多结点元素，更“矮胖”。

2.B+树查询必须查找到叶子结点，B树只要匹配到即可不用管元素位置，因此B+树查找更稳定（并不慢）。

3.对于范围查找来说，B+只需遍历叶子节点链表即可，B树却需要重复地中序遍历。

 

 

在学习HashMap的时候，当桶存储的链表长度大于8时，链表会转变为红黑树，因此学习一下红黑树，在此纪录以备查询。

红黑树

红黑树（Red Black Tree） 是一种自平衡二叉查找树。红黑树和AVL树类似，都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。

它虽然是复杂的，但它的最坏情况运行时间也是非常良好的，并且在实践中是高效的： 它可以在O(log n)时间内做查找，插入和删除，这里的n 是树中元素的数目。

红黑树是每个节点都带有颜色属性的二叉查找树，颜色或红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求:

性质1：节点是红色或黑色。

性质2：根节点是黑色。

性质3：每个叶节点（NIL节点，空节点）是黑色的。

性质4：每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

性质5：从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

从图可以看出，从根节点到每一个叶节点（NIL），都包含了相同数量的黑色节点。

当我们进行插入、删除操作，所做的一切都是为了调整红黑树使之符合这五条性质。

预备知识

1.插入的节点颜色永远为红色

如果插入的节点为黑色，则违反性质5，如果节点为红色，则少违背一条性质，减少代价。

2.左旋和右旋

这个和平衡二叉树的左旋右旋时一致的。

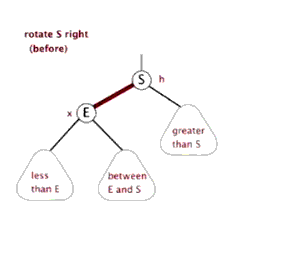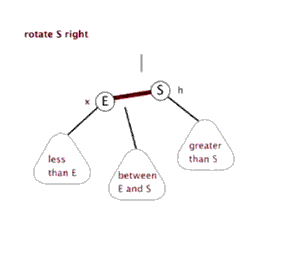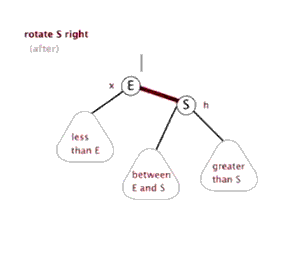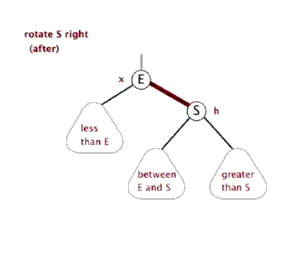
3.节点关系

4.二叉排序树的插入和删除

1.插入：红黑树通过二叉查找树的插入方法来找到要插入的位置。

2.删除：

1.如果删除的是叶节点，可以直接删除； 
2.如果被删除的元素有一个子节点，可以将子节点直接移到被删除元素的位置； 
3.如果要删除节点的左右孩子都存在，则将被删除节点与后继节点（位于被删除节点的右子树上）互换位置，再将被删除节点删除。

插入节点

首先根据二叉查找树的插入方法，找到要插入的位置。

1.插入节点是根节点时

直接涂黑即可，满足五条性质。

2.插入节点的父节点是黑色时

直接插入即可，满足五条性质。

3.①父节点为红色②父节点是祖父节点的左孩子

两种情况：

1.叔叔节点为黑

　　继续细分两种情况：

　　（1）要插入节点是父节点的左孩子

　　　　

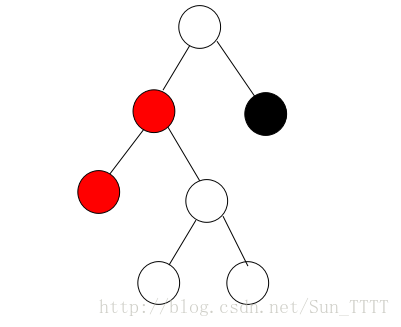
　　　　违反性质4，对应的操作：

　　　　　　1）将祖父节点和父节点的颜色进行互换。

　　　　　　2）将祖父节点进行右旋。

　　

 

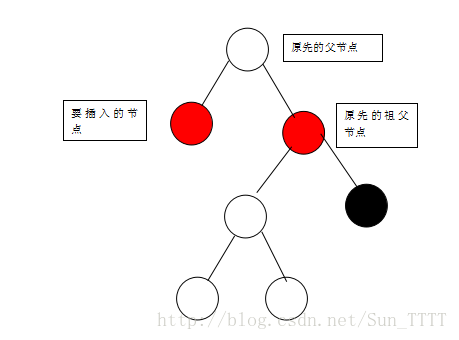
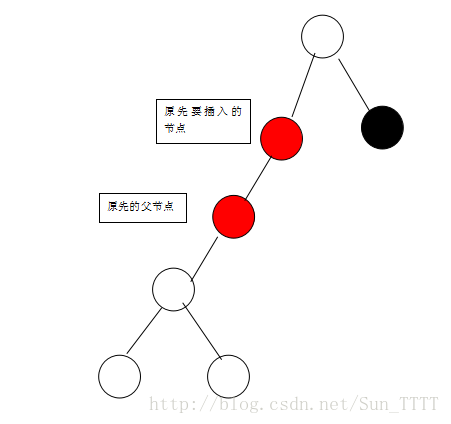
　　（2）要插入节点是父节点的右孩子

 

　　　　　　对应的操作：

　　　　　　1）对父节点进行左旋

　　　　　　2）这是情况转变为上一种情况

　　　　　　

 

　　　　　　　　

2.叔叔节点为红

　　对应操作：

　　　　1）将“父节点”设为黑色。

　　　　2）将“叔叔节点”设为黑色。

　　　　3）将“祖父节点”设为红色。

　　　　4）将“祖父节点”设为“当前节点”（红色节点）。

　　　　5）继续对“当前节点”进行操作。

4.①父节点为红色②父节点是祖父节点的右孩子

　　和上一小节为镜像情况

删除节点

加入颜色之后，被删除元素和后继元素互换只是值的互换，并不互换颜色，这个要注意。

1.当删除的节点是红色时，直接拿其孩子节点补控位即可，性质5仍然满足。

2.当删除的节点是黑色时，性质5被破坏

　　（1）如果该节点的孩子节点为红色时，直接拿孩子节点替换被删除的节点，并将孩子节点染成黑色。

　　（2）如果孩子节点为黑色，分为6种情况。

在对这6中情况进行分析之前，我们先做一些假设，我们删除的节点是X（至多只有一个孩子节点），其孩子节点为N，X的兄弟节点是S，S的左节点为S_L，右节点是S_R。

接下来的讨论是建立在节点X（黑色）已经被删除，节点N已经替换X的基础上进行的。

 

情况一：

要删除的节点X是根节点，且左右孩子节点均为空节点，此时将节点X用空节点替换完成删除操作。

情况二：

S为红色，其他节点为黑色。这种情况下对N的父节点进行左旋操作，然后互换P与S的颜色。但这并未结束，经过节点P和N的路径删除前有3个黑色节点（P -> X -> N），现在只剩两个了（P -> N）。比未经过N的路径少一个黑色节点，性质5仍不满足，还需要继续调整。不过此时可以按照情况四、五、六进行调整。

情况三：

 N 的父节点，兄弟节点 S 和 S 的孩子节点均为黑色。这种情况下可以简单的把 S 染成红色，所有经过 S 的路径比之前少了一个黑色节点，这样经过 N 的路径和经过 S 的路径黑色节点数量一致了。但经过 P 的路径比不经过 P 的路径少一个黑色节点，此时需要从情况一开始对 P 进行平衡处理。

 情况四：

N 的父节点是红色，S 和 S 孩子为黑色。这种情况比较简单，我们只需交换 P 和 S 颜色即可。这样所有通过 N 的路径上增加了一个黑色节点，所有通过 S 的节点的路径必然也通过 P 节点，由于 P 与 S 只是互换颜色，并不影响这些路径。

情况五：

S 为黑色，S 的左孩子为红色，右孩子为黑色。N 的父节点颜色可红可黑，且 N 是 P 左孩子。这种情况下对 S 进行右旋操作，并互换 S 和 SL 的颜色。此时，所有路径上的黑色数量仍然相等，N 兄弟节点的由 S 变为了 SL，而 SL 的右孩子变为红色。接下来我们到情况六继续分析。

情况六：

S 为黑色，S 的右孩子为红色。N 的父节点颜色可红可黑，且 N 是其父节点左孩子。这种情况下，我们对 P 进行左旋操作，并互换 P 和 S 的颜色，并将 SR 变为黑色。因为 P 变为黑色，所以经过 N 的路径多了一个黑色节点，经过 N 的路径上的黑色节点与删除前的数量一致。对于不经过 N 的路径，则有以下两种情况：

1. 该路径经过 N 新的兄弟节点 SL ，那它之前必然经过 S 和 P。而 S 和 P 现在只是交换颜色，对于经过 SL 的路径不影响。
2. 该路径经过 N 新的叔叔节点 SR，那它之前必然经过 P、 S 和 SR，而现在它只经过 S 和 SR。在对 P 进行左旋，并与 S 换色后，经过 SR 的路径少了一个黑色节点，性质5被打破。另外，由于 S 的颜色可红可黑，如果 S 是红色的话，会与 SR 形成连续的红色节点，打破性质4（每个红色节点必须有两个黑色的子节点）。此时仅需将 SR 由红色变为黑色即可同时恢复性质4和性质5（从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。）。

 

 

参考文献

1. B-树（B树）详解

2.《数据结构》— 严蔚敏

3. 红黑树详细分析，看了都说好

4. 最容易懂得红黑树