链表问题

一、打印两个有序链表的公共部分

【题目】

　　给定两个有序链表的头指针head1和head2，打印两个链表的公共部分。

【分析】

　　假设有如下两个有序链表

　　

　　整个流程是这样的：谁小动谁，一开始1<2，所以head1来到3的位置

　　

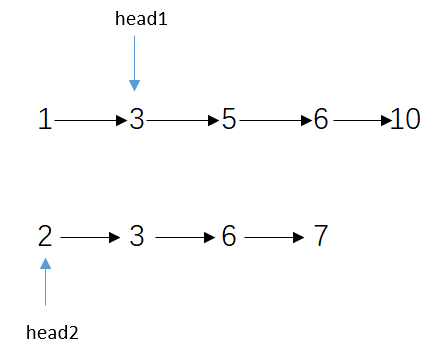
　　此时2<3，所以head2来到3的位置

　　

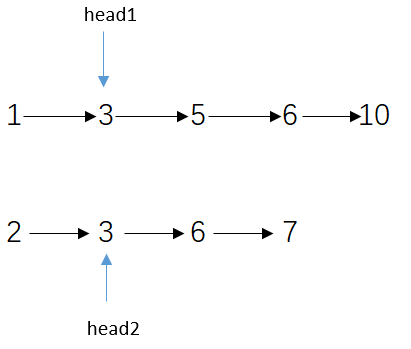
　　head1=head2，打印3，并且head1和head2共同往下走一步

　　

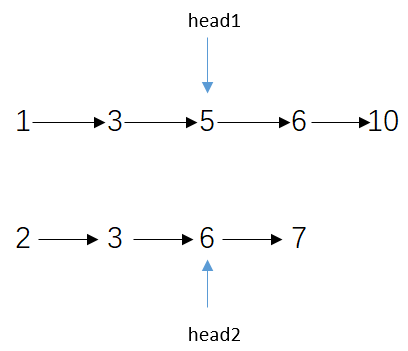
　　重复上述步骤，直到一个指针来到终点位置，整个流程就停止。

　　总结：谁小谁就往右移动，如果相等，打印该数，并共同往右移动；head1和head2只要有1个来到终点位置，整个流程就停止。

【代码实现】

public class PrintCommonPart {
    public static class Node {
        public int value;
        public Node next;

        public Node(int data) {
            this.value = data;
        }
    }

    public static void printCommonPart(Node head1, Node head2) {
        System.out.print("Common Part: ");
        while (head1 != null && head2 != null) {
            if (head1.value < head2.value) {
                head1 = head1.next;
            } else if (head1.value > head2.value) {
                head2 = head2.next;
            } else {
                System.out.print(head1.value + " ");
                head1 = head1.next;
                head2 = head2.next;
            }
        }
        System.out.println();
    }

    public static void printLinkedList(Node node) {
        System.out.print("Linked List: ");
        while (node != null) {
            System.out.print(node.value + " ");
            node = node.next;
        }
        System.out.println();
    }

    public static void main(String[] args) {
        Node node1 = new Node(2);
        node1.next = new Node(3);
        node1.next.next = new Node(5);
        node1.next.next.next = new Node(6);

        Node node2 = new Node(1);
        node2.next = new Node(2);
        node2.next.next = new Node(5);
        node2.next.next.next = new Node(7);
        node2.next.next.next.next = new Node(8);

        printLinkedList(node1);
        printLinkedList(node2);
        printCommonPart(node1, node2);
    }

}

二、判断一个链表是否为回文结构

【题目】

　　给定一个链表的头节点head，请判断该链表是否为回文结构。 例如： 1->2->1，返回true。 1->2->2->1，返回true。15->6->15，返回true。 1->2->3，返回false。

【方法一】——额外空间复杂度O(N)

　　假设有如下链表

　　

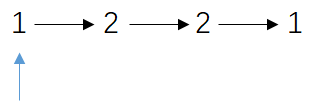
　　每遍历一个数都往栈压入相应的数

　　

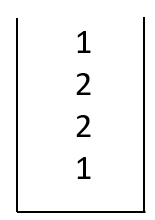
　　因为栈是先进后出的，所以从栈顶到栈底其实就是原来链表顺序的逆序。

　　然后再从头开始遍历链表，每遍历一个数，都从栈中取一个数出来比较，相当于原始顺序跟逆序依次比较，如果比到最后每一步都相等，则该链表是回文的；如果其中有任何一步不相等，就不是回文。

　　这个因为要准备一个栈，所以额外空间是O(N)。

public class IsPalindromeList {
    public static class Node {
        public int value;
        public Node next;

        public Node(int data) {
            this.value = data;
        }
    }

    /**
     * 需要N的额外空间，空间复杂度为O(N)
     * @param head
     * @return
     */
    public static boolean isPalindrome1(Node head) {
        Stack<Node> stack = new Stack<>();
        Node cur = head;
        while (cur != null) {
            stack.push(cur);
            cur = cur.next;
        }
        while (head != null) {
            if (head.value != stack.pop().value) {
                return false;
            }
            head = head.next;
        }
        return true;
    }

　　public static void printLinkedList(Node node) {
        System.out.print("Linked List: ");
        while (node != null) {
            System.out.print(node.value + " ");
            node = node.next;
        }
        System.out.println();
    }

    public static void main(String[] args) {
        Node head = null;
        printLinkedList(head);
        System.out.print(isPalindrome1(head) + " | ");
        printLinkedList(head);
        System.out.println("=========================");

        head = new Node(1);
        printLinkedList(head);
        System.out.print(isPalindrome1(head) + " | ");
        printLinkedList(head);
        System.out.println("=========================");

        head = new Node(1);
        head.next = new Node(2);
        printLinkedList(head);
        System.out.print(isPalindrome1(head) + " | ");
        printLinkedList(head);
        System.out.println("=========================");

        head = new Node(1);
        head.next = new Node(2);
        head.next.next = new Node(3);
        printLinkedList(head);
        System.out.print(isPalindrome1(head) + " | ");
        printLinkedList(head);
        System.out.println("=========================");

        head = new Node(1);
        head.next = new Node(2);
        head.next.next = new Node(2);
        head.next.next.next = new Node(1);
        printLinkedList(head);
        System.out.print(isPalindrome1(head) + " | ");
        printLinkedList(head);
        System.out.println("=========================");
    }
}

【方法二】——额外空间复杂度O(N)

　　设置两个指针，一个快指针（一次走2步），一个慢指针（一次走1步）。

　　快指针走完的时候，慢指针会来到中点的位置；慢指针来到中点位置后，将右半部分压到栈里

　　

　　快指针走完的时候，慢指针来到3的位置，然后将后面的部分（2，1）压到栈里。

　　　　

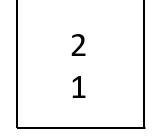
　　然后前面的部分（1，2）和栈中元素比较，如果每一步都相等，就是回文。

　　这个方法的实质就是：假设有一段线，从中点开始，让右半部分折回去，然后每个数再比较，如果每一步都相等，就是回文。

　　

　　用这个方法的好处是：栈会少一半空间，虽然额外空间还是O(N),但实际的结果是省了一半的空间

public class IsPalindromeList {
    public static class Node {
        public int value;
        public Node next;

        public Node(int data) {
            this.value = data;
        }
    }/**
     * 需要n/2的额外空间,但是空间复杂度仍是O(N)
     * @param head
     * @return
     */
    public static boolean isPalindrome2(Node head) {
        if (head == null || head.next == null) {
            return true;
        }
        //慢指针——指向第2个数
        Node slow = head.next;
        //快指针——指向第1个数
        Node fast = head;

        while (fast.next != null && fast.next.next != null) {
            //慢指针一次走一步
            slow = slow.next;
            //快指针一次走两步
            fast = fast.next.next;
        }

        // 上面过程结束之后,slow就是指向中点的后一位.如果是偶数个数的话,那么就是指向后半段的第一个位置
        Stack<Node> stack = new Stack<>();
        while (slow != null) {
            stack.push(slow);
            slow = slow.next;
        }
        while (!stack.isEmpty()) {
            if (head.value != stack.pop().value) {
                return false;
            }
            head = head.next;
        }
        return true;
    }

    public static void printLinkedList(Node node) {
        System.out.print("Linked List: ");
        while (node != null) {
            System.out.print(node.value + " ");
            node = node.next;
        }
        System.out.println();
    }

    public static void main(String[] args) {
        Node head = null;
        printLinkedList(head);
        System.out.print(isPalindrome2(head) + " | ");
        printLinkedList(head);
        System.out.println("=========================");

        head = new Node(1);
        printLinkedList(head);
        System.out.print(isPalindrome2(head) + " | ");
        printLinkedList(head);
        System.out.println("=========================");

        head = new Node(1);
        head.next = new Node(2);
        printLinkedList(head);
        System.out.print(isPalindrome2(head) + " | ");
        printLinkedList(head);
        System.out.println("=========================");

        head = new Node(1);
        head.next = new Node(2);
        head.next.next = new Node(3);
        printLinkedList(head);
        System.out.print(isPalindrome2(head) + " | ");
        printLinkedList(head);
        System.out.println("=========================");

        head = new Node(1);
        head.next = new Node(2);
        head.next.next = new Node(2);
        head.next.next.next = new Node(1);
        printLinkedList(head);
        System.out.print(isPalindrome2(head) + " | ");
        printLinkedList(head);
        System.out.println("=========================");
    }
}

【方法三】——额外空间复杂度O(1)

　　设置两个指针，一个快指针（一次走2步），一个慢指针（一次走1步）
　　快指针走完的时候，慢指针会来到中点的位置。从中点位置开始，让右半部分逆序。

　　

　　然后分别从两边的1开始遍历，往中间逼近，中途有任何一个对不上，就不是回文，如果全部都能对的上，就是回文。
　　但是不管是不是回文，你在返回结果前，都要把后半部分调回原来的样子。

public class IsPalindromeList {
    public static class Node {
        public int value;
        public Node next;

        public Node(int data) {
            this.value = data;
        }
    }/**
     * 彻底不用额外空间
     * @param head
     * @return
     */
    public static boolean isPalindrome3(Node head) {
        if (head == null || head.next == null) {
            return true;
        }
        //慢指针
        Node slow = head;
        //快指针
        Node fast = head;
        /*
        快指针一次走两步,慢指针一次走一步
        当快指针走完后,慢指针来到中间位置
         */
        while (fast.next != null && fast.next.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        //右半部分的第一个元素
        fast = slow.next;
        slow.next = null;
        Node n3 = null;
        /*
        后半部分逆序
         */
        while (fast != null) {
            n3 = fast.next;
            fast.next = slow;
            slow = fast;
            fast = n3;
        }
        n3 = slow;
        fast = head;
        boolean res = true;
        //检查每一步的数是否相等
        while (slow != null && fast != null) {
            if (slow.value != fast.value) {
                res = false;
                break;
            }
            slow = slow.next;
            fast = fast.next;
        }
        slow = n3.next;
        n3.next = null;
        //返回结果之前,将后半部分逆序的部分调回来
        while (slow != null) {
            fast = slow.next;
            slow.next = n3;
            n3 = slow;
            slow = fast;
        }

        return res;
    }

　　public static void printLinkedList(Node node) {
        System.out.print("Linked List: ");
        while (node != null) {
            System.out.print(node.value + " ");
            node = node.next;
        }
        System.out.println();
    }

    public static void main(String[] args) {
        Node head = null;
        printLinkedList(head);
        System.out.print(isPalindrome3(head) + " | ");
        printLinkedList(head);
        System.out.println("=========================");

        head = new Node(1);
        printLinkedList(head);
        System.out.print(isPalindrome3(head) + " | ");
        printLinkedList(head);
        System.out.println("=========================");

        head = new Node(1);
        head.next = new Node(2);
        printLinkedList(head);
        System.out.print(isPalindrome3(head) + " | ");
        printLinkedList(head);
        System.out.println("=========================");

        head = new Node(1);
        head.next = new Node(2);
        head.next.next = new Node(3);
        printLinkedList(head);
        System.out.print(isPalindrome3(head) + " | ");
        printLinkedList(head);
        System.out.println("=========================");

        head = new Node(1);
        head.next = new Node(2);
        head.next.next = new Node(2);
        head.next.next.next = new Node(1);
        printLinkedList(head);
        System.out.print(isPalindrome3(head) + " | ");
        printLinkedList(head);
        System.out.println("=========================");
    }
}

三、将单向链表按某值划分成左边小、中间相等、右边大的形式

【题目】

　　给定一个单向链表的头节点head，节点的值类型是整型，再给定一个整 数pivot。实现一个调整链表的函数，将链表调整为左部分都是值小于 pivot的节点，中间部分都是值等于pivot的节点，右部分都是值大于 pivot的节点。除这个要求外，对调整后的节点顺序没有更多的要求。 例如：链表9->0->4->5->1，pivot=3。 调整后链表可以是1->0->4->9->5，也可以是0->1->9->5->4。总之，满 足左部分都是小于3的节点，中间部分都是等于3的节点（本例中这个部分为空），右部分都是大于3的节点即可。对某部分内部的节点顺序不做要求。

【分析】

　　最简单的做法：
　　把链表的每一个位置放在一个容器里，即生成一个Node类型的数组，然后在数组里面对Node的值进行划分：小于指定值的放左边，等于的放中间，大于的放右边。然后从容器开始重新连接这个链表，连完之后返回即可。此时的额外空间复杂度为O(N)

public class SmallerEqualBigger {
    public static class Node {
        public int value;
        public Node next;

        public Node(int data) {
            this.value = data;
        }
    }

    public static Node listPartition1(Node head, int pivot) {
        if (head == null) {
            return head;
        }
        Node cur = head;
        int i = 0;
        while (cur != null) {
            i++;
            cur = cur.next;
        }
        Node[] nodeArr = new Node[i];
        i = 0;
        cur = head;
        //将原链表的每个Node节点放在数组里
        for (i = 0; i != nodeArr.length; i++) {
            nodeArr[i] = cur;
            cur = cur.next;
        }
        arrPartition(nodeArr, pivot);
        //从数组容器里重新连接成链表结构
        for (i = 1; i != nodeArr.length; i++) {
            nodeArr[i - 1].next = nodeArr[i];
        }
        nodeArr[i - 1].next = null;
        return nodeArr[0];
    }

    /**
     * 等同于荷兰国旗问题
     * @param nodeArr
     * @param pivot
     */
    public static void arrPartition(Node[] nodeArr, int pivot) {
        int small = -1;
        int big = nodeArr.length;
        int index = 0;
        while (index != big) {
            if (nodeArr[index].value < pivot) {
                swap(nodeArr, ++small, index++);
            } else if (nodeArr[index].value == pivot) {
                index++;
            } else {
                swap(nodeArr, --big, index);
            }
        }
    }

    public static void swap(Node[] nodeArr, int a, int b) {
        Node tmp = nodeArr[a];
        nodeArr[a] = nodeArr[b];
        nodeArr[b] = tmp;
    }

    public static void printLinkedList(Node node) {
        System.out.print("Linked List: ");
        while (node != null) {
            System.out.print(node.value + " ");
            node = node.next;
        }
        System.out.println();
    }

    public static void main(String[] args) {
        Node head1 = new Node(7);
        head1.next = new Node(9);
        head1.next.next = new Node(1);
        head1.next.next.next = new Node(8);
        head1.next.next.next.next = new Node(5);
        head1.next.next.next.next.next = new Node(2);
        head1.next.next.next.next.next.next = new Node(5);
        printLinkedList(head1);
        head1 = listPartition1(head1, 4);
        printLinkedList(head1);
    }
}

【进阶】—— 在原问题的要求之上再增加如下两个要求。
　　在左、中、右三个部分的内部也做顺序要求，要求每部分里的节点从左 到右的顺序与原链表中节点的先后次序一致。 例如：链表9->0->4->5->1，pivot=3。调整后的链表是0->1->9->4->5。 在满足原问题要求的同时，左部分节点从左到右为0、1。在原链表中也 是先出现0，后出现1；中间部分在本例中为空，不再讨论；右部分节点 从左到右为9、4、5。在原链表中也是先出现9，然后出现4，最后出现5。如果链表长度为N，时间复杂度请达到O(N)，额外空间复杂度请达到O(1)。

【分析】

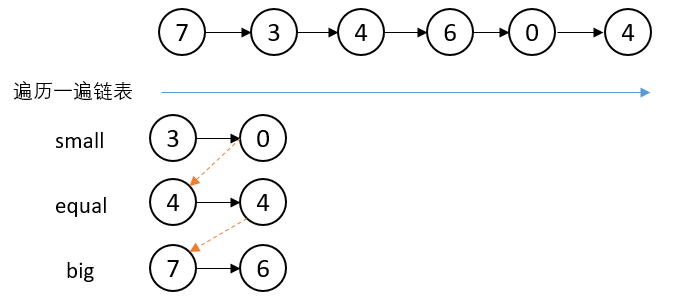
　　假设有如下链表，按照4来划分，设置3个引用(small、equal、big)。

　　遍历一次链表，找到第一个小于4的节点，找到第一个等于4的节点，找到第一个大于4的节点.。
　　再遍历一遍链表，如果找到的是某个区域的头节点，就省略，比如说再遍历的时候找到的是7，就省略，因为这个7和big之前找到的节点是同一个(注意这里比较的是Node的内存地址，而不是Node的值)。遍历到6的时候，6>4，就往大于的区域里放，依次下去。然后再将3个区域连接起来即可

　　

public class SmallerEqualBigger {
    public static class Node {
        public int value;
        public Node next;

        public Node(int data) {
            this.value = data;
        }
    }/**
     * 不需要额外的空间复杂度，且能达到稳定性
     * @param head
     * @param pivot
     * @return
     */
    public static Node listPartition2(Node head, int pivot) {
        if (head == null) {
            return null;
        }
        //小于部分链表的head和tail
        Node sH = null, sT = null;
        //等于部分链表的head和tail
        Node eH = null, eT = null;
        //大于部分链表的head和tail
        Node bH = null, bT = null;

        //用来保存下一个结点
        Node next = null;

        //划分到三个不同的链表
        while (head != null) {
            next = head.next;
            //为了链表拼接后,最后一个就不用再去赋值其next域为null了
            head.next = null;
            //向small部分　分布
            if (head.value < pivot) {
                //small部分的第一个结点
                if (sH == null) {
                    sH = head;
                    sT = head;
                } else {
                    //把head放到small最后一个
                    sT.next = head;
                    //更新small部分的sT
                    sT = head;
                }
            } else if (head.value == pivot) {
                if (eH == null) {
                    eH = head;
                    eT = head;
                } else {
                    eT.next = head;
                    eT = head;
                }
            } else {
                if (bH == null) {
                    bH = head;
                    bT = head;
                } else {
                    bT.next = head;
                    bT = next;
                }
            }
            head = next;
        }

        ///将三个链表合并(注意边界的判断)
        if (sT != null) {
            //合并small和equal部分
            sT.next = eH;
            eT = eT == null ? sT : eT;
        }
        if (eT != null) {
            eT.next = bH;
        }
        return sH != null ? sH : eH != null ? eH : bH;
    }
　　
　　public static void printLinkedList(Node node) {
        System.out.print("Linked List: ");
        while (node != null) {
            System.out.print(node.value + " ");
            node = node.next;
        }
        System.out.println();
    }

    public static void main(String[] args) {
        Node head1 = new Node(7);
        head1.next = new Node(3);
        head1.next.next = new Node(4);
        head1.next.next.next = new Node(6);
        head1.next.next.next.next = new Node(0);
        head1.next.next.next.next.next = new Node(4);
        printLinkedList(head1);
        head1 = listPartition2(head1, 4);
        printLinkedList(head1);
    }
}

四、复制含有随机指针节点的链表

【题目】

　　一种特殊的链表节点类描述如下：

public class Node {
    public int value;
    public Node next;
    public Node rand;

    public Node(int data) {
        this.value = data;
    }
}

　　Node类中的value是节点值，next指针和正常单链表中next指针的意义一 样，都指向下一个节点，rand指针是Node类中新增的指针，这个指针可能指向链表中的任意一个节点，也可能指向null。 给定一个由Node节点类型组成的无环单链表的头节点head，请实现一个函数完成这个链表中所有结构的复制，并返回复制的新链表的头节点。

【分析】

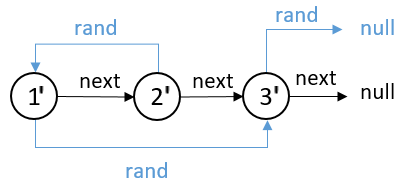
　　这题的题意是，假设有下面链表，节点1的next指向2，节点2的next指向3，节点3的next指向null。另外，假设节点1的rand指针指向节点3，节点2的rand指针指向节点1，节点3的rand指针指向null。

　　

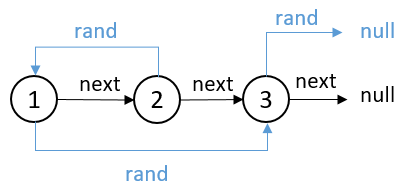
　　需要做的是：复制该链表的所有结构（深度拷贝），最后返回1'节点

　　

　　我们可以用HashMap来实现，具体做法是：

　　从节点1开始依次遍历到节点3，每遍历一个节点，就克隆出一个新的节点，并把这2个节点放在HashMap中，key是原链表节点，value是新链表节点。

　　怎么实现克隆呢？如果一个节点是node，克隆后的节点为newNode，可以将node节点传入newNode节点中：Node newNode=new Node(node.value)；

　　但是现在对于newNode来说，next指针和rand指针都是null。怎么办呢？我们可以在hash表里记一个记录，例如key就是节点1，value就是节点1’。

　　

　　再次遍历原始链表，当我得到节点1的时候，在map中可以把节点1‘取出；因为节点1的next指针是指向节点2的，所以拷贝后的节点1‘的next指针也应该指向节点2’。而在map中，我们可以通过节点2找到节点2‘，所以就可以将1’的next指针指向2‘；我们还可以通过节点1的rand指针找到节点3，节点1’的rand指针也应该指向3'节点，其中3‘节点可以在map中找到。这是在遍历节点1的时候，1’的指针是怎么设置的。按照此方式设置2‘和3’的指针。

public class CopyListWithRandom {
    public static class Node {
        public int value;
        public Node next;
        public Node rand;

        public Node(int data) {
            this.value = data;
        }
    }

    /**
     * 利用HashMap,key存的是原链表的节点,value存的是该节点的克隆节点
     * @param head
     * @return
     */
    public static Node copyListWithRand1(Node head) {
        HashMap<Node, Node> map = new HashMap<>();
        Node cur = head;
        while (cur != null) {
            //map的value里面是纯净的节点,开始是没有next跟rand的指向,需要自己去指定
            map.put(cur, new Node(cur.value));
            cur = cur.next;
        }
        Node X = head;
        //以下while跑完后,克隆节点之间的结构就设置完毕了
        while (X != null) {
            // map.get(x)是x的拷贝节点x'
            map.get(X).next = map.get(X.next);
            map.get(X).rand = map.get(X.rand);
            X = X.next;
        }
        return map.get(head);
    }

    public static void printRandLinkedList(Node head) {
        Node cur = head;
        System.out.print("Order: ");
        while (cur != null) {
            System.out.print(cur.value + " ");
            cur = cur.next;
        }
        System.out.println();
        cur = head;
        System.out.print("rand: ");
        while (cur != null) {
            System.out.print(cur.rand == null ? "- " : cur.rand.value + " ");
            cur = cur.next;
        }
        System.out.println();
    }

    public static void main(String[] args) {
        Node head = null;
        Node res = null;
        printRandLinkedList(head);
        res = copyListWithRand1(head);
        printRandLinkedList(res);
        printRandLinkedList(head);
        System.out.println("=========================");

        head = new Node(1);
        head.next = new Node(2);
        head.next.next = new Node(3);
        head.next.next.next = new Node(4);
        head.next.next.next.next = new Node(5);
        head.next.next.next.next.next = new Node(6);

        head.rand = head.next.next.next.next.next; // 1 -> 6
        head.next.rand = head.next.next.next.next.next; // 2 -> 6
        head.next.next.rand = head.next.next.next.next; // 3 -> 5
        head.next.next.next.rand = head.next.next; // 4 -> 3
        head.next.next.next.next.rand = null; // 5 -> null
        head.next.next.next.next.next.rand = head.next.next.next; // 6 -> 4

        printRandLinkedList(head);
        res = copyListWithRand1(head);
        printRandLinkedList(res);
        printRandLinkedList(head);
        System.out.println("=========================");
    }
}

【进阶】
　　不使用额外的数据结构，只用有限几个变量，且在时间复杂度为 O(N)内完成原问题要实现的函数。

【分析】

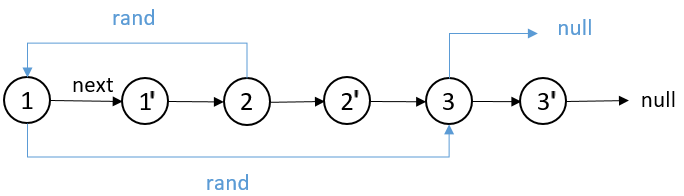
　　不用hash表又怎么做呢？还是这个链表，但是拷贝后的节点是放在老链表的下一个，然后再和老链表的下一个相连。注意rand指针原来的位置并没变，只是在原来的节点1和节点2之间加了一个节点1‘。

　　

　　这样做有什么好处呢？接下来遍历的时候，每一次遍历拿出2个节点，比如拿出节点1和节点1‘。1通过rand指针可以找到3，而3的克隆节点3’就是3的下一个节点，在这种结构中，通过3的next就可以找到3‘，然后把1’的rand指向3‘。第一种方法使用hash表的目的就是为了知道老链表和新链表的对应关系，而用这种方法也能把新老链表的对应关系留下来。按照这种思路，依次拿出节点2和节点2’，节点3和节点3‘即可实现所求。

　　

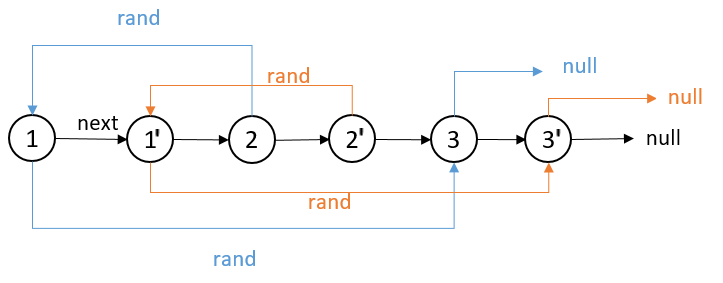
　　最后再将新链表和老链表分离出来，整个过程就结束了。

public class CopyListWithRandom {
    public static class Node {
        public int value;
        public Node next;
        public Node rand;

        public Node(int data) {
            this.value = data;
        }
    }public static Node copyListWithRand2(Node head) {
        if (head == null) {
            return null;
        }
        Node cur = head;
        Node next = null;

        //复制链表
        //原来的链表 : 1 -> 2 -> 3 -> 4 -> 5 -> 6
        //复制的链表 : 1 -> 1' -> 2 -> 2' -> 3-> 3' -> 4 -> 4' -> 5 -> 5' -> 6 -> 6'
        while (cur != null) {
            next = cur.next;
            cur.next = new Node(cur.value);
            cur.next.next = next;
            cur = next;
        }
        cur = head;
        //curCopy相当于是一个引线
        Node curCopy = null;

        //设置随机指向
        while (cur != null) {
            next = cur.next.next;
            curCopy = cur.next;
            //注意curCopy的rand指向的是rand.next.因为原节点的next才是纯净的节点,这些next节点到时需要分隔出去
            curCopy.rand = cur.rand != null ? cur.rand.next : null;
            cur = next;
        }
        //这个节点就是分隔出来的链表的头节点
        Node res = head.next;
        cur = head;

        //分离
        while (cur != null) {
            next = cur.next.next;
            curCopy = cur.next;
            //这一步是连接后面的
            cur.next = next;
            curCopy.next = next != null ? next.next : null;
            cur = next;
        }
        return res;
    }

    public static void printRandLinkedList(Node head) {
        Node cur = head;
        System.out.print("Order: ");
        while (cur != null) {
            System.out.print(cur.value + " ");
            cur = cur.next;
        }
        System.out.println();
        cur = head;
        System.out.print("rand: ");
        while (cur != null) {
            System.out.print(cur.rand == null ? "- " : cur.rand.value + " ");
            cur = cur.next;
        }
        System.out.println();
    }

    public static void main(String[] args) {
        Node head = null;
        Node res = null;
        printRandLinkedList(head);
        res = copyListWithRand2(head);
        printRandLinkedList(res);
        printRandLinkedList(head);
        System.out.println("=========================");

        head = new Node(1);
        head.next = new Node(2);
        head.next.next = new Node(3);
        head.next.next.next = new Node(4);
        head.next.next.next.next = new Node(5);
        head.next.next.next.next.next = new Node(6);

        head.rand = head.next.next.next.next.next; // 1 -> 6
        head.next.rand = head.next.next.next.next.next; // 2 -> 6
        head.next.next.rand = head.next.next.next.next; // 3 -> 5
        head.next.next.next.rand = head.next.next; // 4 -> 3
        head.next.next.next.next.rand = null; // 5 -> null
        head.next.next.next.next.next.rand = head.next.next.next; // 6 -> 4

        printRandLinkedList(head);
        res = copyListWithRand2(head);
        printRandLinkedList(res);
        printRandLinkedList(head);
        System.out.println("=========================");
    }
}

五、两个单链表相交的一系列问题

【题目】

　　在本题中，单链表可能有环，也可能无环。给定两个单链表的头节点 head1和head2，这两个链表可能相交，也可能不相交。请实现一个函数， 如果两个链表相交，请返回相交的第一个节点；如果不相交，返回null 即可。 要求：如果链表1的长度为N，链表2的长度为M，时间复杂度请达到 O(N+M)，额外空间复杂度请达到O(1)。

【分析】

　　先解决一个问题：怎么判断一个链表是否有环？如果一个链表有环，返回第一个入环的节点；如果一个链表无环，返回null；

　　方法一：使用hash表。

　　在遍历过程中，把每个节点放到hashSet里（没有value，只有key），如果有环的话，就能重复回到一个节点。因为set把你遍历过的节点都放到里面去了，所以就能发现一个节点有没有遍历过。如果发现一个节点有遍历过，就是有环，并且返回第一个入环的节点；如果走到null，就是无环，返回null。注意：set里面存的不是节点的值，而是节点的内存地址。

/**
 * 返回链表的第一个入环节点——使用HashSet，需要额外空间
 * @param head
 * @return
 */
public static Node getFirstLoopNode(Node head) {
    HashSet<Node> set = new HashSet<>();
    while (head != null) {
        if (set.contains(head)) {
            return head;
        }
        set.add(head);
        head = head.next;
    }
    return null;
}

　　方法二：不用额外空间，准备两个指针，一个快指针，一个慢指针。

　　快指针一次走2步，慢指针一次走1步。如果走的过程中，快指针走到了null，肯定无环；如果有环，快指针和慢指针一定会在环上相遇（相遇并不是值相等，而是内存地址是同一个）。相遇后，快指针回到开头，然后变成每次走一步；接下来，快指针和慢指针一起走，它们会在第一个入环节点处相遇，这是一个数学结论。此过程时间复杂度还是O(N).

　　

/**
 * 返回链表的第一个入环节点——使用快慢指针，不需要额外空间
 * @param head
 * @return
 */
public static Node getLoopNode(Node head) {
    if (head == null || head.next == null || head.next.next == null) {
        return null;
    }
    Node slow = head.next;
    Node fast = head.next.next;
    while (slow != fast) {
        if (fast.next == null || fast.next.next == null) {
            return null;
        }
        fast = fast.next.next;
        slow = slow.next;
    }
    //快指针和慢指针相遇后,快指针回到头部
    fast = head;
    while (slow != fast) {
        slow = slow.next;
        fast = fast.next;
    }
    return slow;
}

　　现在有两个链表，head1是链表1的头节点，head2是链表2的头节点，调用getLoopNode()函数后，就可以得到head1的第一个入环节点loop1， 也能得到head2整个链表中第一个入环节点loop2，如果loop1=null&&loop2=null，这就是两个无环链表的相交问题。两个无环链表的相交问题有两种可能：一种是不相交，一种是相交

　　 

　　假如有两个无环链表h1、h2，怎么求两条无环链表相交的第一个节点？

　　方法一：使用hash表

　　hash表遍历h1，把h1上的所有节点都加到set里去，然后在遍历h2的过程中,每遍历一个节点，都检查该节点是否存在于set中，如果存在，这个节点就是和h1相交的第一个节点。
　　举个例子，第一遍把左侧h1的节点全部放到set中，然后依次遍历右侧的h2节点，前两个节点set中都不存在 ，来到第三个节点时，发现在set中，所以这个节点就是第一个相交的节点。

　　

　　方法二：不使用hash表

　　两个无环链表h1和h2。先遍历h1，因为是无环，所以能找到结尾，统计h1的长度(len1)以及找到h1最后一个节点(e1)。再遍历h2，统计h2的长度(len2)并找到h2最后一个节点(e2)，如果e1和e2不是同一个节点，那么h1和h2不可能相交，返回null。如果e1=e2，h1和h2肯定相交，那它俩第一个相交的节点是什么呢？举个例子，如果len1=100,len2=80，还是让h1和h2都从头开始遍历，但是让h1先走20步，然后和h2一起往下走，它俩一定会共同进入第一个相交的节点。

　　

/**
 * 两个链表都无环
 * @param head1
 * @param head2
 * @return 返回第一个相交的节点
 */
public static Node noLoop(Node head1, Node head2) {
    if (head1 == null || head2 == null) {
        return null;
    }
    Node cur1 = head1;
    Node cur2 = head2;
    int n = 0;
    while (cur1.next != null) {
        n++;
        cur1 = cur1.next;
    }
    while (cur2.next != null) {
        n--;
        cur2 = cur2.next;
    }
    //如果最后一个节点不相等,不可能相交,即无环
    if (cur1 != cur2) {
        return null;
    }
    cur1 = n > 0 ? head1 : head2;
    cur2 = cur1 == head1 ? head2 : head1;
    n = Math.abs(n);
    while (n != 0) {
        n--;
        cur1 = cur1.next;
    }
    while (cur1 != cur2) {
        cur1 = cur1.next;
        cur2 = cur2.next;
    }
    return cur1;
}

　　如果一个链表有环，另外一个链表无环，不可能相交。如果有相交，都会破坏单链表只有一个next的结构。

　　如果两个链表都有环，即loop1!=null，loop2!=null。形成的结构有3种：

　　

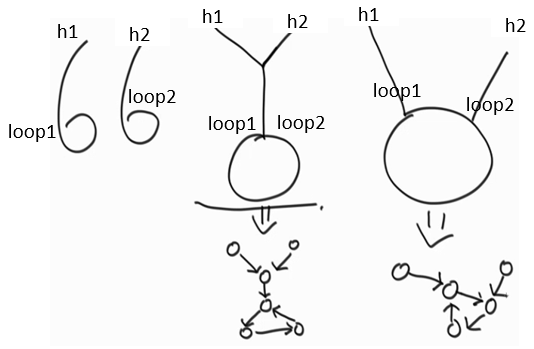
　　怎么判断是哪一种结构？

　　如果loop1=loop2，是第二种结构。怎么求相交的第一个节点？把环里的部分忽略掉，把loop1、loop2作为终止，这时候就等同于两个无环链表的相交问题；

　　如果loop1!=loop2，让loop1通过next指针往下走，因为loop1是第一个入环的节点，它往下走一定能回到自己，如果它回到自己了，都没有遇到loop2，就是第一种结构；

　　如果loop1往下走后，中途遇到了loop2，就是第三种情况。如果中途能遇到loop2，返回loop1作为第一个相交的节点或者返回loop2作为第一个相交的节点都对，因为loop1是距离h1更近的，loop2是距离h2更近的，它们都可以叫做h1和h2两个链表第一个相交的节点。

/**
 * 两个链表都有环
 * @param head1
 * @param loop1 head1的第一个入环节点
 * @param head2
 * @param loop2 head2的第一个入环节点
 * @return
 */
public static Node bothLoop(Node head1, Node loop1, Node head2, Node loop2) {
    Node cur1 = null;
    Node cur2 = null;
    //如果是第二种结构,把环里的部分忽略掉,把loop1、loop2作为终止,等同于两个无环链表的相交问题
    if (loop1 == loop2) {
        cur1 = head1;
        cur2 = head2;
        int n = 0;
        while (cur1 != loop1) {
            n++;
            cur1 = cur1.next;
        }
        while (cur2 != loop2) {
            n--;
            cur2 = cur2.next;
        }
        cur1 = n > 0 ? head1 : head2;
        cur2 = cur1 == head1 ? head2 : head1;
        n = Math.abs(n);
        while (n != 0) {
            n--;
            cur1 = cur1.next;
        }
        while (cur1 != cur2) {
            cur1 = cur1.next;
            cur2 = cur2.next;
        }
        return cur1;
    } else {
        //如果loop1!=loop2,让loop1通过next指针往下走
        cur1 = loop1.next;
        while (cur1 != loop1) {
            //如果loop1走的过程中遇到loop2,就是第三种情况
            if (cur1 == loop2) {
                return loop1;
            }
            cur1 = cur1.next;
        }
        return null;
    }
}

【两个链表相交系列问题的代码实现】

public class FindFirstIntersectNode {
    public static class Node {
        public int value;
        public Node next;

        public Node(int data) {
            this.value = data;
        }
    }

    public static Node getIntersectNode(Node head1, Node head2) {
        if (head1 == null || head2 == null) {
            return null;
        }
        //head1的第一个入环节点
        Node loop1 = getLoopNode(head1);
        //head2的第一个入环节点
        Node loop2 = getLoopNode(head2);
        //两个无环链表的相交问题
        if (loop1 == null && loop2 == null) {
            return noLoop(head1, head2);
        }
        //两个有环链表的相交问题
        if (loop1 != null && loop2 != null) {
            return bothLoop(head1, loop1, head2, loop2);
        }
        return null;
    }public static void main(String[] args) {
        // head1链表:1->2->3->4->5->6->7->null
        Node head1 = new Node(1);
        head1.next = new Node(2);
        head1.next.next = new Node(3);
        head1.next.next.next = new Node(4);
        head1.next.next.next.next = new Node(5);
        head1.next.next.next.next.next = new Node(6);
        head1.next.next.next.next.next.next = new Node(7);

        // head2链表:0->9->8->6->7->null
        Node head2 = new Node(0);
        head2.next = new Node(9);
        head2.next.next = new Node(8);
        //head2的8节点指向head1的6节点
        head2.next.next.next = head1.next.next.next.next.next;
        //打印两个无环链表的第一个相交节点,结果为6
        System.out.println(getIntersectNode(head1, head2).value);

        // head1链表：1->2->3->4->5->6->7->4...
        head1 = new Node(1);
        head1.next = new Node(2);
        head1.next.next = new Node(3);
        head1.next.next.next = new Node(4);
        head1.next.next.next.next = new Node(5);
        head1.next.next.next.next.next = new Node(6);
        head1.next.next.next.next.next.next = new Node(7);
        //7节点的next指向4节点,形成有环
        head1.next.next.next.next.next.next = head1.next.next.next;

        // 0->9->8->2...
        head2 = new Node(0);
        head2.next = new Node(9);
        head2.next.next = new Node(8);
        //head2的8节点的next指针指向head1的2节点
        head2.next.next.next = head1.next;
        //两个有环链表的相交问题(第二种结构)
        System.out.println(getIntersectNode(head1, head2).value);

        // head2链表：0->9->8->6->4->5->6..
        head2 = new Node(0);
        head2.next = new Node(9);
        head2.next.next = new Node(8);
        //head2的8节点的next指针指向head1的6节点
        head2.next.next.next = head1.next.next.next.next.next;
        //两个有环链表的相交问题(第三种结构),返回loop1或loop2
        System.out.println(getIntersectNode(head1, head2).value);
    }

}