递归
一、剖析递归行为
举个简单的例子来理解递归，以及系统上递归是怎么实现的。假设有个功能：在整个数组中找最大值。
这本是一个很简单的功能，我们可以直接用遍历的方式来完成。但如果把它改成递归的形式，又会是怎么样的呢？
递归思路：将数组分为左边L和右边R两个部分，L边的最大值为max左，R边的最大值为max右，max左和max右最大的一个，就是全局最大值。
1 public class Test { 2 public static int getMax(int[] arr, int L, int R) { 3 //终止条件 4 if (L == R) { 5 return arr[L]; 6 } 7 8 int mid = (L + R) / 2; 9 int maxLeft = getMax(arr, L, mid); 10 int maxRight = getMax(arr, mid + 1, R); 11 return Math.max(maxLeft, maxRight); 12 } 13 14 public static void main(String[] args) { 15 int[] arr = {4, 3, 2, 1}; 16 System.out.println(getMax(arr, 0, arr.length - 1)); 17 } 18 }
以上就是我们的递归行为，那么我们该如何理解它呢？在系统上这个递归函数到底是怎么跑的？下面我们来剖析这个问题：
已知给出的数组arr长度为4，程序一开始调用的是第16行的getMax(arr,0,3)，这个函数在系统里面就会被生成。那么函数的实质是什么呢，自己调用自己的过程又是什么意思？其实，递归函数就是系统帮你压栈。
刚开始调用getMax()函数时，L=0,R=3，程序来到第8行，产生了一个变量：mid=1；而maxLeft参数指望着它的子过程getMax(arr,L,mid)给它返回，系统上是怎么做到的呢？实际上，它把getMax()的所有信息，压到系统的一个栈里面，栈里记录了getMax()函数当前跑到的行数（第9行），还记录了这个函数中的所有参数(0和3)以及所有的变量(mid)：
然后调用子过程getMax(arr,0,1)，这个过程继续进入我们的代码，此时L=0,R=1，mid=0，程序继续来到第9行，调用getMax(arr,0,0)。在调用子过程的时候，会把getMax(arr,0,1)这个子函数所有的信息（行数、参数、内部所有的变量）全部压到栈里：
然后调的是子过程getMax(arr,0,0)，接着这个子过程开始执行，之前的过程全部在栈里。这时候L=0,R=0，达到终止条件，直接返回arr[0]，值为4。那么getMax(arr,0,0)这个函数返回之后，我怎么知道现在该跑哪个函数呢？从栈里面，把栈顶的过程取出来，彻底还原现场，你当时把一个函数压栈了，就相当于你保护了这个函数的所有现场，所有的信息都记录下来了。把系统的栈中拿出这个函数所有的信息进行重构，变成当前需要的返回值的那一行。
将
弹出，知道跑的是getMax(arr,0,1)这个过程，也知道此时mid=0，还知道跑的是第9行。就会接着getMax(arr,0,1)这个过程从第9行开始往下跑，maxLeft就接收到了子过程的返回值(4)。然后又会生成一个maxLeft的变量，值为4。程序来到第10行，又调用了一个子过程，会把当前的信息重新压到栈里
然后调用子过程，子过程返回后，再从栈中取出信息，还原现场，让刚才的返回值被一 个新的变量接住，再进行判断。。。
所谓的递归函数，就是系统栈。“自己调用自己"其实是逻辑概念上的解释。
递归函数是有实际落地的结构的，一个函数在调用子过程之前，会把自己的所有过程全部压到栈里去，信息完全保存，子过程返回之后，会利用这些信息彻底还原现场继续跑，跑完之后再从栈中拿出一个函数，再次还原现场，最终串起所有子过程和父过程的通信。
所以有一句话，任何递归行为都可以改为非递归行为，如果不让系统帮你压栈，自己进行压栈，那这时递归就变成迭代了。
二、递归行为时间复杂度的估算
master公式的使用： T(N) = a*T(N/b) + O(N^d) ——估计递归行为复杂度的通式。
其中，T(N)指的是样本量大小为N的情况下的时间复杂度，T就是time的首字母。N/b是子过程的样本量，a是子过程发生的次数；O(N^d)表示，除去调用子过程之外，剩下的时间复杂度。
我们再以上面求最大值的流程为例，来解释一下master公式
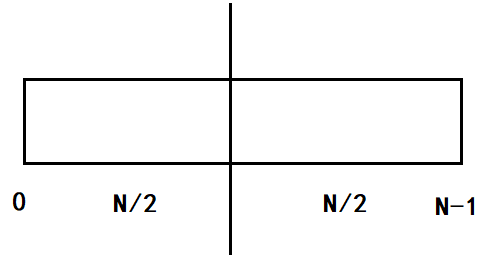
0到N-1范围上切一半，左边部分求一个最大值，右边部分求一个最大值，两个最大值比较作为整体的解。整个时间复杂度就是T(N)，左边切一半，样本量是N/2，右边切一半，样本量是N/2，左边跑完跑右边，所以样本量为N/2的过程发生了2次。当你跑完子过程后，比较较大的并且返回，这是一个常数操作，时间复杂度为O（1）。所以有T(N)=2T(N/2)+O(1)，将此表达式与master公式比较，可知此处的b=2，a=2，d=0。
只要是满足 T(N) = a*T(N/b) + O(N^d)这种表达式的，一律有公式来求出对应的复杂度。
- log(b,a) > d -> 复杂度为O(N^log(b,a))
比如T(N)=2T(N/2)+O(1)，b=2，a=2，d=0；带入得，log(2,2)=1>d=0,所以复杂度就是O(N^log(b,a))=O(N)
- log(b,a) = d -> 复杂度为O(N^d * logN)
如果某流程的表达式是T(N)=2T(N/2)+O(N)，那么它的复杂度就是O(N*logN)
- log(b,a) < d -> 复杂度为O(N^d)
【注意】
master公式也是有适用范围的——划分的子过程规模必须是一样的情况下才能使用。T(N)=T(N/5)+T(2/3N)+O(N²）就不能用master公式来求解，需要用数学方式来证明的，不必掌握。
