常见的比较排序
一、冒泡排序(Bubble Sort)
【原理】
比较两个相邻的元素,将值大的元素交换至右端。
【思路】
依次比较相邻的两个数,将小数放在前面,大数放在后面。即在第一趟:首先比较第1个和第2个数,将小数放前,大数放后。然后比较第2个数和第3个数,将小数放前,大数放后,如此继续,直至比较最后两个数,将小数放前,大数放后。重复第一趟步骤,直至全部排序完成。
第一趟比较完成后,最后一个数一定是数组中最大的一个数,所以第二趟比较的时候最后一个数不参与比较;
第二趟比较完成后,倒数第二个数也一定是数组中第二大的数,所以第三趟比较的时候最后两个数不参与比较;
依次类推,每一趟比较次数-1;
……
【举例】——要排序数组:int[] arr={6,3,8,2,9,1};
第一趟排序:
第一次排序:6和3比较,6大于3,交换位置: 3 6 8 2 9 1
第二次排序:6和8比较,6小于8,不交换位置:3 6 8 2 9 1
第三次排序:8和2比较,8大于2,交换位置: 3 6 2 8 9 1
第四次排序:8和9比较,8小于9,不交换位置:3 6 2 8 9 1
第五次排序:9和1比较:9大于1,交换位置: 3 6 2 8 1 9
第一趟总共进行了5次比较, 排序结果: 3 6 2 8 1 9
---------------------------------------------------------------------
第二趟排序:
第一次排序:3和6比较,3小于6,不交换位置:3 6 2 8 1 9
第二次排序:6和2比较,6大于2,交换位置: 3 2 6 8 1 9
第三次排序:6和8比较,6大于8,不交换位置:3 2 6 8 1 9
第四次排序:8和1比较,8大于1,交换位置: 3 2 6 1 8 9
第二趟总共进行了4次比较, 排序结果: 3 2 6 1 8 9
---------------------------------------------------------------------
第三趟排序:
第一次排序:3和2比较,3大于2,交换位置: 2 3 6 1 8 9
第二次排序:3和6比较,3小于6,不交换位置:2 3 6 1 8 9
第三次排序:6和1比较,6大于1,交换位置: 2 3 1 6 8 9
第二趟总共进行了3次比较, 排序结果: 2 3 1 6 8 9
---------------------------------------------------------------------
第四趟排序:
第一次排序:2和3比较,2小于3,不交换位置:2 3 1 6 8 9
第二次排序:3和1比较,3大于1,交换位置: 2 1 3 6 8 9
第二趟总共进行了2次比较, 排序结果: 2 1 3 6 8 9
---------------------------------------------------------------------
第五趟排序:
第一次排序:2和1比较,2大于1,交换位置: 1 2 3 6 8 9
第二趟总共进行了1次比较, 排序结果: 1 2 3 6 8 9
---------------------------------------------------------------------
最终结果:1 2 3 6 8 9
---------------------------------------------------------------------
由此可见:N个数字要排序完成,总共进行N-1趟排序,每i趟的排序次数为(N-i)次,所以可以用双重循环语句,外层控制循环多少趟,内层控制每一趟的循环次数,即
for(int i=1;i<arr.length;i++){ for(int j=1;j<arr.length-i;j++){ //交换位置 }
冒泡排序的优点:每进行一趟排序,就会少比较一次,因为每进行一趟排序都会找出一个较大值。如上例:第一趟比较之后,排在最后的一个数一定是最大的一个数,第二趟排序的时候,只需要比较除了最后一个数以外的其他的数,同样也能找出一个最大的数排在参与第二趟比较的数后面,第三趟比较的时候,只需要比较除了最后两个数以外的其他的数,以此类推……也就是说,每进行一趟比较,每一趟少比较一次,一定程度上减少了算法的量。
用时间复杂度来说:
1.如果我们的数据正序,只需要走一趟即可完成排序。所需的比较次数C和记录移动次数M均达到最小值,即:Cmin=n-1;Mmin=0;所以,冒泡排序最好的时间复杂度为O(n)。
2.如果很不幸我们的数据是反序的,则需要进行n-1趟排序。每趟排序要进行n-i次比较(1≤i≤n-1),且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下,比较和移动次数均达到最大值:
冒泡排序的最坏时间复杂度为:O(n2) 。
综上所述:冒泡排序总的平均时间复杂度为:O(n2) 。
【代码实现】
public class BubbleSort { public static void main(String[] args) { int[] arr = {6, 3, 8, 2, 9, 1}; System.out.println("排序前数组:"); for (int num : arr) { System.out.println(num + " "); } for (int i = 0; i < arr.length - 1; i++) {//外层循环控制排序趟数 for (int j = 0; j < arr.length - 1 - i; j++) {//内层循环控制每一趟排序多少次 if (arr[j] > arr[j + 1]) { swap(arr, j, j + 1); } } } System.out.println("------------"); System.out.println("排序后数组:"); for (int num : arr) { System.out.println(num + " "); } } public static void swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; } }
二、选择排序(SelectionSort)
【原理】
每一趟从待排序的记录中选出最小的元素,顺序放在已排好序的序列最后,直到全部记录排序完毕。也就是:每一趟在n-i+1(i=1,2,…n-1)个记录中选取关键字最小的记录作为有序序列中第i个记录。
【基本思想】(简单选择排序)
给定数组:int[] arr={里面n个数据};第1趟排序,在待排序数据arr[1]~arr[n]中选出最小的数据,将它与arrr[1]交换;第2趟,在待排序数据arr[2]~arr[n]中选出最小的数据,将它与arr[2]交换;以此类推,第i趟在待排序数据arr[i]~arr[n]中选出最小的数据,将它与arr[i]交换,直到全部排序完成。
【举例】——数组 int[] arr={5,2,8,4,9,1};
第一趟排序:
最小数据1,把1放在首位,也就是1和5互换位置,
排序结果:1 2 8 4 9 5
-------------------------------------------------------
第二趟排序:
第1以外的数据{2 8 4 9 5}进行比较,2最小,
排序结果:1 2 8 4 9 5
-------------------------------------------------------
第三趟排序:
除1、2以外的数据{8 4 9 5}进行比较,4最小,8和4交换
排序结果:1 2 4 8 9 5
-------------------------------------------------------
第四趟排序:
除第1、2、4以外的其他数据{8 9 5}进行比较,5最小,8和5交换
排序结果:1 2 4 5 9 8
-------------------------------------------------------
第五趟排序:
除第1、2、4、5以外的其他数据{9 8}进行比较,8最小,8和9交换
排序结果:1 2 4 5 8 9
-------------------------------------------------------
注:每一趟排序获得最小数的方法:for循环进行比较,定义一个第三个变量temp,首先前两个数比较,把较小的数放在temp中,然后用temp再去跟剩下的数据比较,如果出现比temp小的数据,就用它代替temp中原有的数据。
【代码实现】
public class SelectionSort { public static void main(String[] args) { int[] arr = {5, 2, 8, 4, 9, 1}; System.out.println("交换之前:"); for (int num : arr) { System.out.print(num + " "); } // 做第i趟排序 for (int i = 0; i < arr.length - 1; i++) { int minIndex = i; // 选最小的记录 for (int j = i + 1; j < arr.length; j++) { //记下目前找到的最小值所在的位置 minIndex = arr[j] < arr[minIndex] ? j : minIndex; } swap(arr, i, minIndex); } System.out.println(); System.out.println("交换后:"); for (int num : arr) { System.out.print(num + " "); } } public static void swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; } }
选择排序的时间复杂度:简单选择排序的比较次数与序列的初始排序无关。 假设待排序的序列有n个元素,则比较次数永远都是n (n - 1) / 2。而移动次数与序列的初始排序有关。当序列正序时,移动次数最少,为 0。当序列反序时,移动次数最多,为3n (n - 1) / 2。
所以,综上,简单排序的时间复杂度为 O(n²)。
三、插入排序(Insertion sort)
插入排序对于少量元素的排序是很高效的,而且这个排序的手法在每个人生活中也是有的哦。你可能没有意识到,当你打牌的时候,就是用的插入排序。
【概念】
从桌上的牌堆摸牌,牌堆内是杂乱无序的,但是我们摸上牌的时候,却会边摸边排序,借用一张算法导论的图。
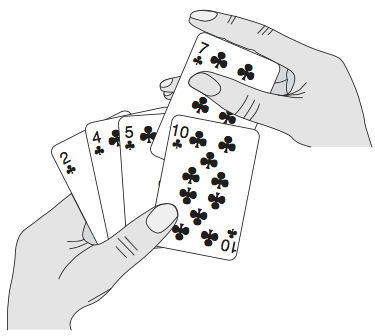
每次我们从牌堆摸起一张牌,然后将这张牌插入我们左手捏的手牌里面,在插入手牌之前,我们会自动计算将牌插入什么位置,然后将牌插入到这个计算后的位置,虽然这个计算转瞬而过,但我们还是尝试分析一下这个过程:
- 我决定摸起牌后,最小的牌放在左边,摸完后,牌面是从左到右依次增大
- 摸起第1张牌,直接捏在手里,现在还不用排序
- 摸起第2张牌,查看牌面大小,如果第二张牌比第一张牌大,就放在右边
- 摸起第3张牌,从右至左开始计算,先看右边的牌,如果摸的牌比最右边的小,那再从右至左看下一张,如果仍然小,继续顺延,直到找到正确位置(循环)
- 摸完所有的牌,结束
所以我们摸完牌,牌就已经排完序了。讲起来有点拗口,但是你在打牌的时候绝对不会觉得这种排序算法会让你头疼。这就是传说中的插入排序。
想象一下,假如我们认为左手拿的牌和桌面的牌堆就是同一数组,当我们摸完牌以后,我们就完成了对这个数组的排序。
【示例】
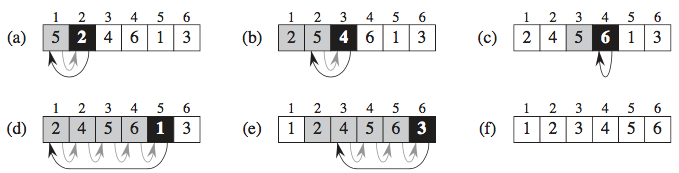
上图就是插入排序的过程,我们把它想象成摸牌的过程。
格子上方的数字:表示格子的序号,图(a)中,1号格子内的数字是5,2号格子是2,3号格子是4,以此类推
灰色格子:我们手上已经摸到的牌
黑色格子:我们刚刚摸起来的牌
白色格子:桌面上牌堆的牌
1、图(a),我们先摸起来一张5,然后摸起来第二张2,发现2比5小,于是将5放到2号格子,2放到1号格子(简单的人话:将2插到5前面)
2、图(b),摸起来一张4,比较4和2号格子内的数字5,4比5小,于是将5放到3号格子,再比较4和1号格子内的2,4大于2,4小于5,于是这就找到了正确的位置。(说人话:就是摸了张4点,将4和5交换位置)
3、图(c)、图(d)、图(e)和图(f),全部依次类推,相信打牌的你能够看懂。
看到这里,我相信应该没人看不懂什么是插入排序了,那么插入排序的代码长什么模样:
【代码实现】
public class InsertionSort { public static void main(String[] args) { int[] arr = {1, 2, 3, 7, 5, 2, 3, 3, 1}; System.out.println("排序前:"); for (int num : arr) { System.out.print(num + " "); } //插入排序 for (int i = 1; i < arr.length; i++) { for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) { swap(arr, j, j + 1); } } System.out.println(); System.out.println("排序后:"); for (int num : arr) { System.out.print(num + " "); } } public static void swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; } }
【时间复杂度】
- 最好情况下,数组已经是有序的,每插入一个元素,只需要考查前一个元素,因此最好情况下,插入排序的时间复杂度为
O(N)。 - 在最坏情况下,数组完全逆序,插入第2个元素时要考察前1个元素,插入第3个元素时,要考虑前2个元素,……,插入第N个元素,要考虑前
N - 1个元素。因此,最坏情况下的比较次数是1 + 2 + 3 + ... + (N - 1),等差数列求和,结果为N² / 2,所以最坏情况下的复杂度为O(N²)。
当数据状况不同,产生的算法流程不同的时候,一律按最差的估计,所以插入排序是O(N²)的算法。
四、归并排序(MERGE-SORT)
【基本思想】
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。

可以看到这种结构很像一棵完全二叉树,本文的归并排序我们采用递归去实现(也可采用迭代的方式去实现)。分阶段可以理解为就是递归拆分子序列的过程,递归深度为log2n。
【合并相邻有序子序列】
再来看看治阶段,我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤。
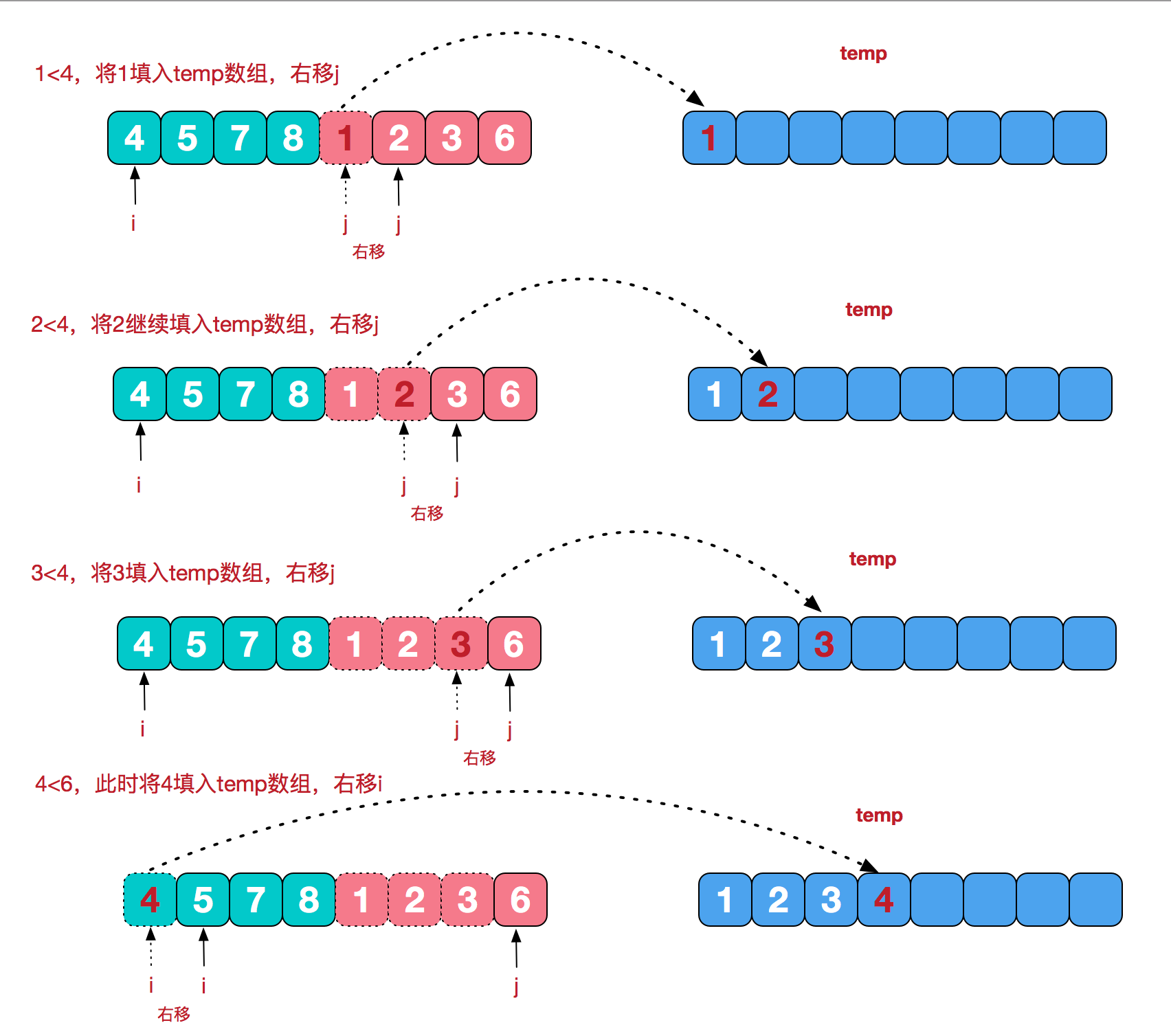
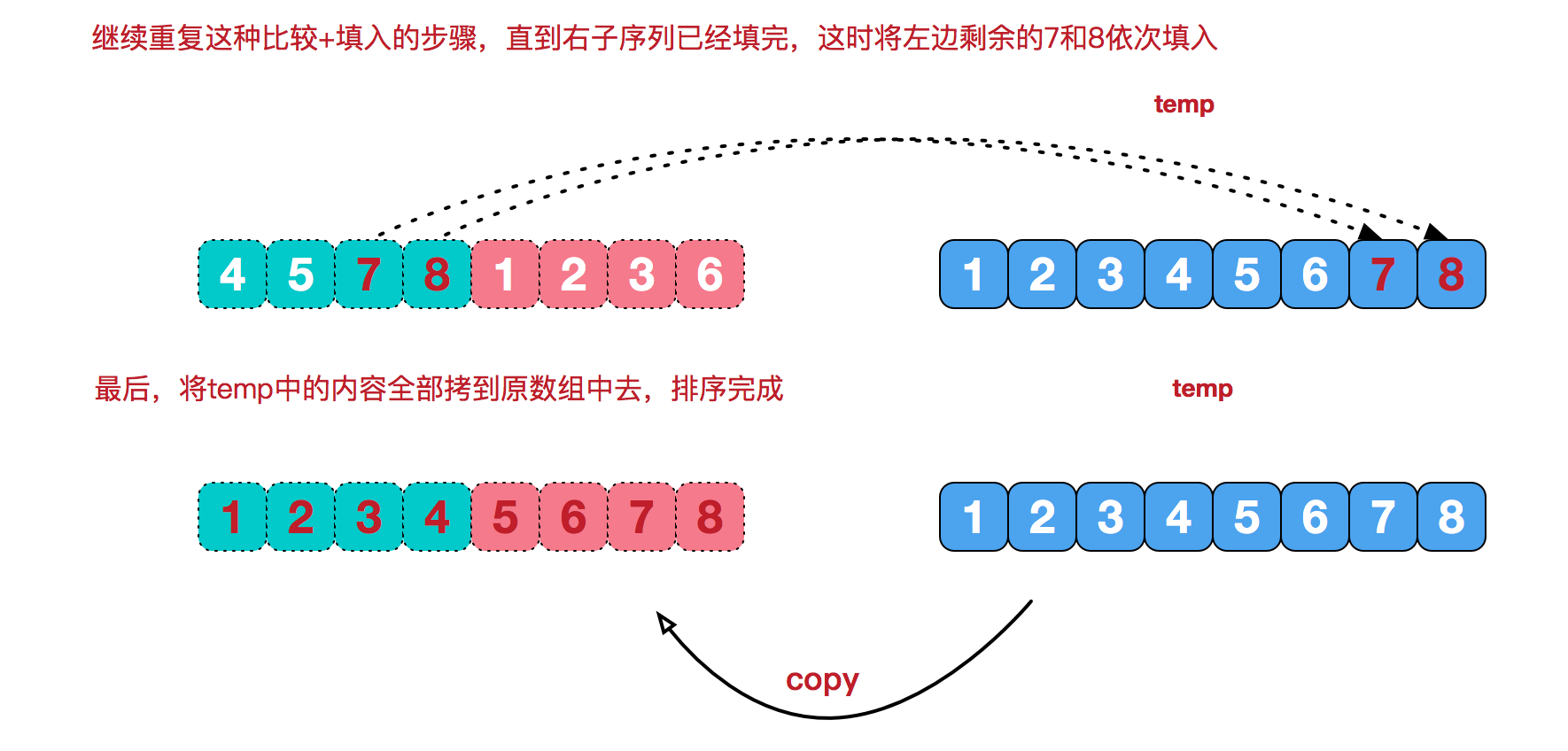
【代码实现】
public class MergeSort { public static void mergeSort(int[] arr) { if (arr == null || arr.length < 2) { return; } sortProcess(arr, 0, arr.length - 1); } public static void sortProcess(int[] arr, int L, int R) { if (L == R) { return; } //L和R中点的位置,相当于(L+R)/2 int mid = L + ((R - L) >> 1); //左边归并排序,使得左子序列有序 sortProcess(arr, L, mid); //右边归并排序,使得右子序列有序 sortProcess(arr, mid + 1, R); //将两个有序子数组合并操作 merge(arr, L, mid, R); } public static void merge(int[] arr, int L, int mid, int R) { int[] temp = new int[R - L + 1]; int i = 0; //左序列指针 int p1 = L; //右序列指针 int p2 = mid + 1; while (p1 <= mid && p2 <= R) { temp[i++] = arr[p1] < arr[p1] ? arr[p1++] : arr[p2++]; } //两个必有且只有一个越界,即以下两个while只会发生一个 //p1没越界,潜台词是p2必越界 while (p1 <= mid) { //将左边剩余元素填充进temp中 temp[i++] = arr[p1++]; } while (p2 <= R) { //将右序列剩余元素填充进temp中 temp[i++] = arr[p2++]; } //将辅助数组temp中的的元素全部拷贝到原数组中 for (int j = 0; j < temp.length; j++) { arr[L + j] = temp[j]; } } public static void main(String[] args) { int[] arr = {9, 8, 7, 6, 5, 4, 3, 2, 1}; mergeSort(arr); System.out.println(Arrays.toString(arr)); } }
【时间复杂度】
根据归并排序的流程,可以看出整个流程的时间复杂度的表达式为:T(N)=2T(N/2)+O(N),所以归并排序的时间复杂度为O(N*logN)
五、快速排序
5.1 经典快速排序
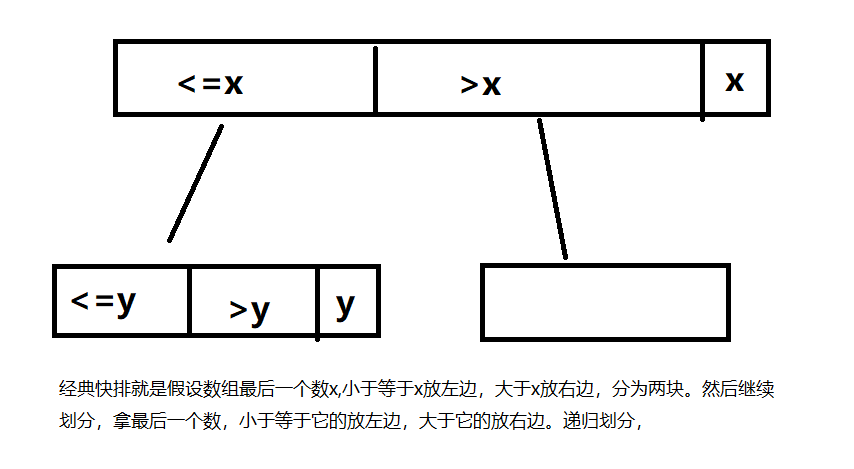
其中就小于等于的区域可以优化一下,小于的放小于区域,等于的放等于区域,大于的放大于区域。这就演变成荷兰国旗问题了。
【荷兰国旗问题】
给定一个数组arr,和一个数num,请把小于num的数放在数组的左边,等于num的数放在数组的中间,大于num的数放在数组的 右边。
大致过程如图:
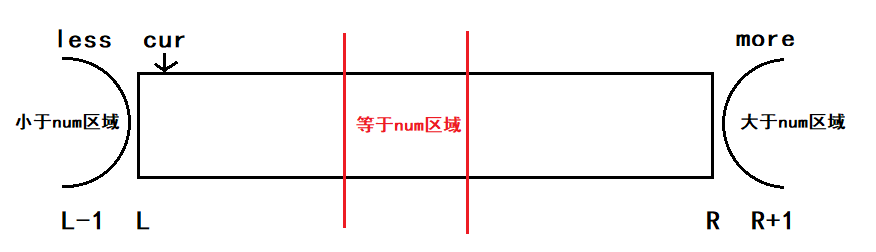
当前数小于num时,该数与小于区域的下一个数交换,小于区域+1;当前数等于num时,继续比较下一个;当前数大于num时,该数与大于区域的前一个数交换,指针不变,继续比较当前位置。
代码如下:
public class NetherlandsFlag { public static int[] partition(int[] arr, int L, int R, int num) { int less = L - 1; int more = R + 1; int cur = L; while (cur < more) { if (arr[cur] < num) { //当前数小于num时,当前数和小于区域的下一个数交换,然后小于区域扩1位置,cur往下跳 swap(arr, ++less, cur++); } else if (arr[cur] > num) { //当前数大于num时,大于区域的前一个位置的数和当前的数交换,且当前数不变,继续比较 swap(arr, --more, cur); } else { //当前数等于num时,直接下一个比较 cur++; } } //返回等于区域的范围 //less+1是等于区域的第一个数 //more-1是等于区域的最后一个数 return new int[]{less + 1, more - 1}; } public static void swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; } // for test public static int[] generateArray() { int[] arr = new int[10]; for (int i = 0; i < arr.length; i++) { arr[i] = (int) (Math.random() * 3); } return arr; } // for test public static void printArray(int[] arr) { if (arr == null) { return; } for (int i = 0; i < arr.length; i++) { System.out.print(arr[i] + " "); } System.out.println(); } public static void main(String[] args) { int[] test = generateArray(); printArray(test); int[] res = partition(test, 0, test.length - 1, 1); printArray(test); System.out.println(res[0]); System.out.println(res[1]); } }
5.2 随机快速排序(优化版)
【基本思想】
从一个数组中随机选出一个数N,通过一趟排序将数组分割成三个部分:小于N的区域;等于N的区域 ;大于N的区域,然后再按照此方法对小于区的和大于区分别递归进行,从而达到整个数据变成有序数组。
【图解流程】
下面通过实例数组进行排序,存在以下数组
从上面的数组中,随机选取一个数(假设这里选的数是5)与最右边的7进行交换 ,如下图
准备一个小于区和大于区(大于区包含最右侧的一个数)等于区要等最后排完数才会出现,并准备一个指针,指向最左侧的数,如下图
到这里,我们要开始排序了,每次操作我们都需要拿指针位置的数与我们选出来的数进行比较,比较的话就会出现三种情况,小于,等于,大于。三种情况分别遵循下面的交换原则:
- 指针的数<选出来的数
1.1 拿指针位置的数与小于区右边第一个数进行交换 1.2 小于区向右扩大一位 1.3 指针向右移动一位
- 选出来的数=选出来的数
2.1 指针向右移动一位
- 指针的数>选出来的数
3.1 拿指针位置的数与大于区左边第一个数进行交换 3.2 大于区向左扩大一位 3.3 指针位置不动
根据上面的图可以看出5=5,满足交换原则第2点,指针向右移动一位,如下图
从上图可知,此时3<5,根据交换原则第1点,拿3和5(小于区右边第一个数)交换,小于区向右扩大一位,指针向右移动一位,结果如下图

从上图可以看出,此时7>5,满足交换原则第3点,7和2(大于区左边第一个数)交换,大于区向左扩大一位,指针不动,如下图
从上图可以看出,2<5,满足交换原则第1点,2和5(小于区右边第一个数)交换,小于区向右扩大一位,指针向右移动一位,得到如下结果
从上图可以看出,6>5,满足交换原则第3点 ,6和6自己换,大于区向左扩大一位,指针位置不动,得到下面结果
此时,指针与大于区相遇,则将指针位置的数6与随机选出来的5进行交换,就可以得到三个区域:小于区,等于区,大于区,如下:
到此,一趟排序结束了,后面再将小于区和大于区重复刚刚的流程即可得到有序的数组。
【代码实现】
public class QuickSort { public static void quickSort(int[] arr) { if (arr == null || arr.length < 2) { return; } quickSort(arr, 0, arr.length - 1); } public static void quickSort(int[] arr, int L, int R) { if (L < R) { //随机产生一个数和最右边的数交换 swap(arr, L + (int) (Math.random() * (R - L + 1)), R); int[] p = partition(arr, L, R); //p[0] - 1表示等于区域的左边界 quickSort(arr, L, p[0] - 1); //p[1] + 1表示等于区域的右边界 quickSort(arr, p[1] + 1, R); } } public static int[] partition(int[] arr, int L, int R) { int less = L - 1; int more = R; while (L < more) { if (arr[L] < arr[R]) { swap(arr, ++less, L++); } else if (arr[L] > arr[R]) { swap(arr, --more, L); } else { L++; } } swap(arr, more, R); return new int[]{less + 1, more}; } public static void swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; } // for test public static void comparator(int[] arr) { Arrays.sort(arr); } // for test public static int[] generateRandomArray(int maxSize, int maxValue) { int[] arr = new int[(int) ((maxSize + 1) * Math.random())]; for (int i = 0; i < arr.length; i++) { arr[i] = (int) ((maxValue + 1) * Math.random()) - (int) (maxValue * Math.random()); } return arr; } // for test public static int[] copyArray(int[] arr) { if (arr == null) { return null; } int[] res = new int[arr.length]; for (int i = 0; i < arr.length; i++) { res[i] = arr[i]; } return res; } // for test public static boolean isEqual(int[] arr1, int[] arr2) { if ((arr1 == null && arr2 != null) || (arr1 != null && arr2 == null)) { return false; } if (arr1 == null && arr2 == null) { return true; } if (arr1.length != arr2.length) { return false; } for (int i = 0; i < arr1.length; i++) { if (arr1[i] != arr2[i]) { return false; } } return true; } // for test public static void printArray(int[] arr) { if (arr == null) { return; } for (int i = 0; i < arr.length; i++) { System.out.print(arr[i] + " "); } System.out.println(); } public static void main(String[] args) { int testTime = 50000; int maxSize = 10; int maxValue = 100; boolean succeed = true; for (int i = 0; i < testTime; i++) { int[] arr1 = generateRandomArray(maxSize, maxValue); int[] arr2 = copyArray(arr1); quickSort(arr1); comparator(arr2); if (!isEqual(arr1, arr2)) { succeed = false; printArray(arr1); printArray(arr2); } } System.out.println(succeed ? "Nice!" : "error~~"); int[] arr = generateRandomArray(maxSize, maxValue); printArray(arr); quickSort(arr); printArray(arr); } }
【时间复杂度】
快排的时间复杂度O(N*logN),空间复杂度O(logN) 【因为每次都是随机事件,坏的情况和差的情况,是等概率的,根据数学期望值可以算出时间复杂度和空间复杂度】,不稳定性排序
六、堆排序
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序 ,要知道堆排序的原理我们首先一定要知道什么是堆。
6.1 什么是堆
这里,必须引入一个完全二叉树的概念,然后过渡到堆的概念。

上图,就是一个完全二叉树,其特点在于:
1.叶子节点只可能在层次最大的两层出现;
2.对于最大层次中的叶子节点,都依次排列在该层的最左边的位置上;
3.如果有度为1的叶子节点,只可能有1个,且该节点只有左孩子而没有右孩子。
那么,完全二叉树与堆有什么关系呢?
我们假设有一棵完全二叉树,在满足作为完全二叉树的基础上,每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。如下图:

同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子

该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
ok,了解了这些定义。接下来,我们来看看堆排序的基本思想及基本步骤。
6.2 堆排序基本思想及步骤
【基本思想】
将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
【步骤】
第一步:构造初始堆。将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。
假设给定无序序列结构如下

此时我们从最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点 arr.length/2-1=5/2-1=1,也就是下面的6结点),从左至右,从下至上进行调整。

找到第二个非叶节点4,由于[4,9,8]中9元素最大,4和9交换。

这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6。
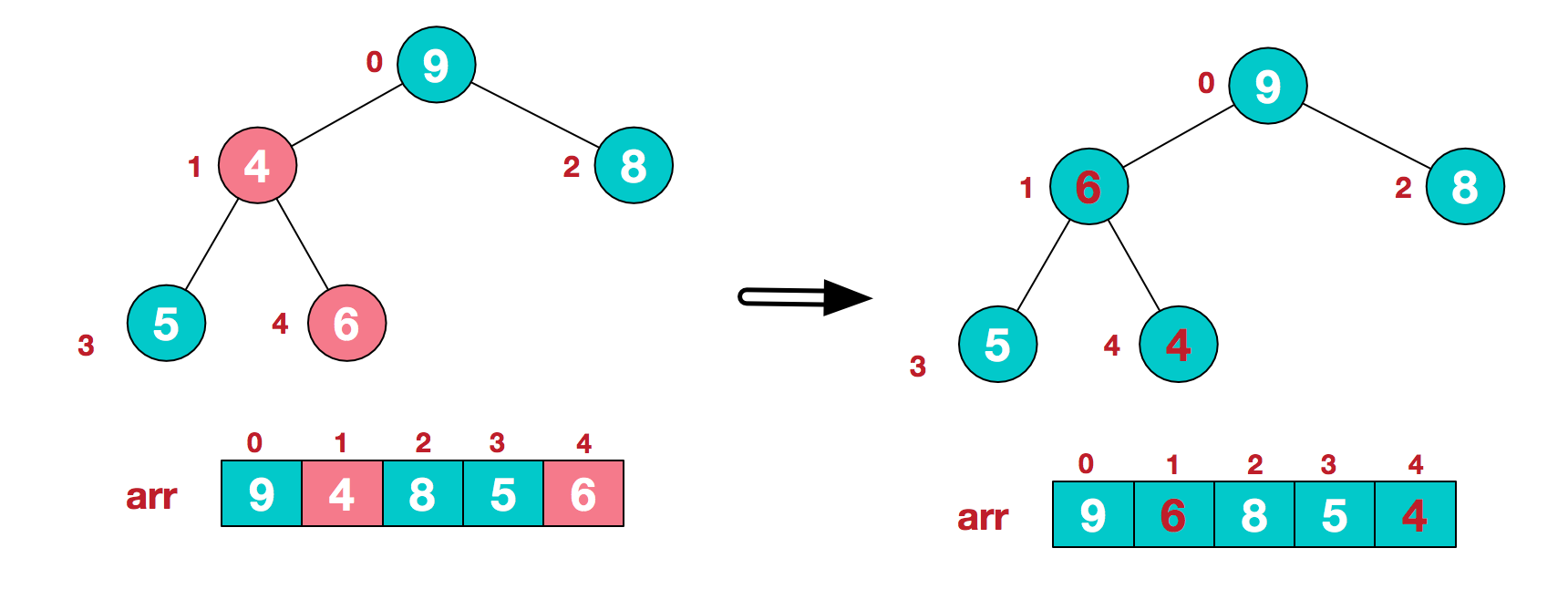
此时,我们就将一个无需序列构造成了一个大顶堆。
第二步:将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
将堆顶元素9和末尾元素4进行交换
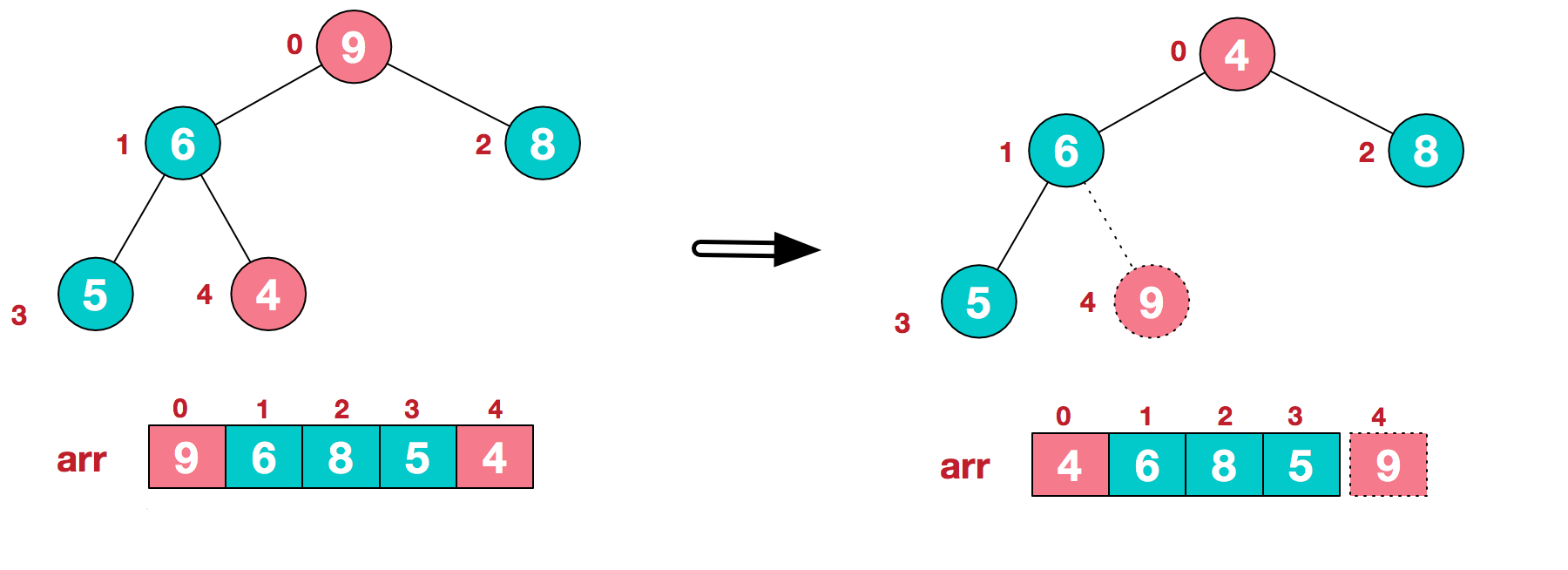
重新调整结构,使其继续满足堆定义
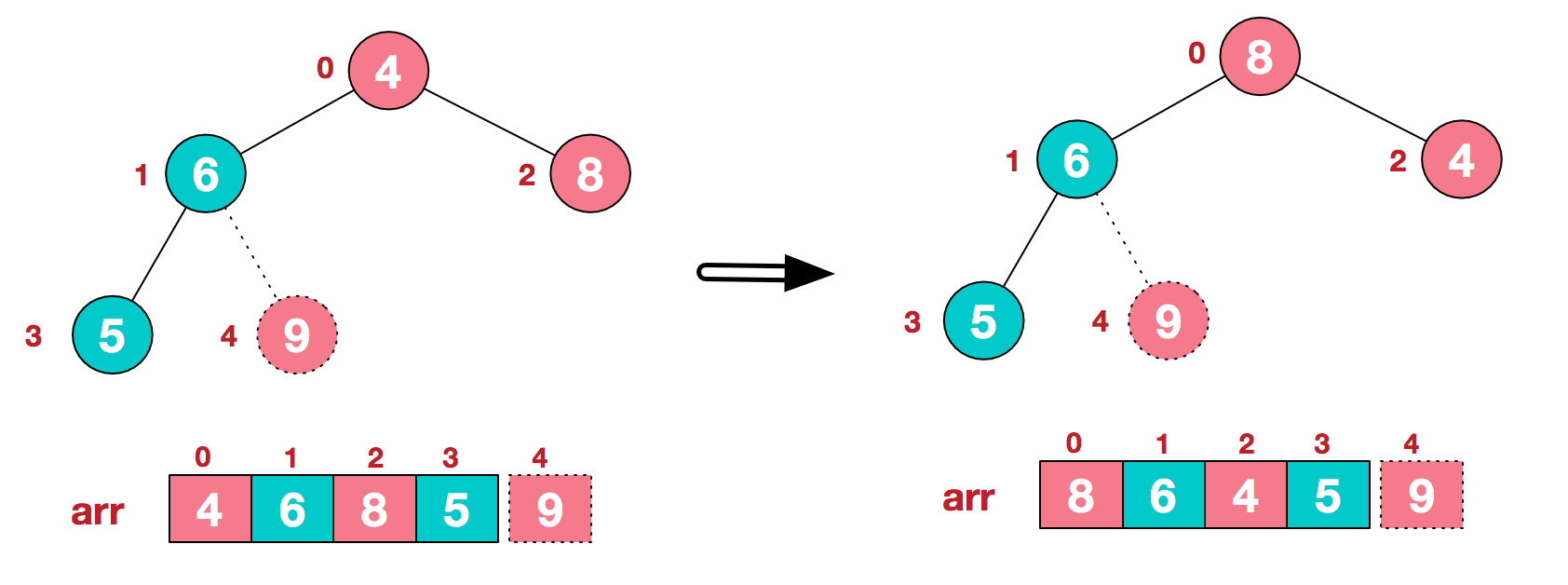
再将堆顶元素8与末尾元素5进行交换,得到第二大元素8.

后续过程,继续进行调整,交换,如此反复进行,最终使得整个序列有序

再简单总结下堆排序的基本思路:
a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
6.3 代码实现
/** * 堆排序代码实现 * @author yi */ public class HeapSort { public static void heapSort(int[] arr) { if (arr == null || arr.length < 2) { return; } //建立大顶堆 for (int i = 0; i < arr.length; i++) { heapInsert(arr, i); } int heapSize = arr.length; //最后一个位置的数和0位置的数交换 swap(arr, 0, --heapSize); while (heapSize > 0) { //从0位置开始,将当前形成的堆调成大顶堆 heapify(arr, 0, heapSize); swap(arr, 0, --heapSize); } } /** * 建立大顶堆,时间复杂度为O(N) * @param arr * @param index */ public static void heapInsert(int[] arr, int index) { //如果当前数比父节点大 while (arr[index] > arr[(index - 1) / 2]) { //和父节点交换 swap(arr, index, (index - 1) / 2); //index往上跑 index = (index - 1) / 2; } } /** * 调整大顶堆(仅是调整过程,建立在大顶堆已构建的基础上) * 一个值变小,往下"沉"的操作 * * @param arr * @param index * @param heapSize 堆的大小 */ public static void heapify(int[] arr, int index, int heapSize) { //左孩子 int left = index * 2 + 1; //左孩子在堆上是存在的,没越界 while (left < heapSize) { //left+1:右孩子 //右孩子没越界,且右孩子的值比左孩子大时,那么较大的数就是右孩子的值所在的位置;反之... //largest表示左右孩子谁的值更大,谁的下标就是largest int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left; //找到左右孩子两者的较大值后,再拿这个值和当前数比较,哪个大哪个就作为largest的下标 largest = arr[largest] > arr[index] ? largest : index; if (largest == index) { //如果你和你的孩子之间的最大值是你自己,不用再往下"沉"了 break; } //当前数和左右孩子之间较大的数交换 swap(arr, largest, index); index = largest; left = index * 2 + 1; } } public static void swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; } public static void main(String[] args) { int[] arr = {3, 5, 2, 1, 6, 7, 3, 9}; System.out.println(Arrays.toString(arr)); heapSort(arr); System.out.println(Arrays.toString(arr)); } }
【时间复杂度】
- 初始化堆的过程:O(n)
- 调整堆的过程:O(nlogn)
综上所述:堆排序的时间复杂度为:O(nlogn)
七、排序算法的稳定性及其意义
7.1 稳定性的定义
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
7.2 稳定性的意义
- 如果只是简单的进行数字的排序,那么稳定性将毫无意义。
- 如果排序的内容仅仅是一个复杂对象的某一个数字属性,那么稳定性依旧将毫无意义
- 如果要排序的内容是一个复杂对象的多个数字属性,但是其原本的初始顺序毫无意义,那么稳定性依旧将毫无意义。
- 除非要排序的内容是一个复杂对象的多个数字属性,且其原本的初始顺序存在意义,那么我们需要在二次排序的基础上保持原有排序的意义,才需要使用到稳定性的算法,例如要排序的内容是一组原本按照价格高低排序的对象,如今需要按照销量高低排序,使用稳定性算法,可以使得想同销量的对象依旧保持着价格高低的排序展现,只有销量不同的才会重新排序。(当然,如果需求不需要保持初始的排序意义,那么使用稳定性算法依旧将毫无意义)。
7.3 常见的排序算法的稳定性分析
【冒泡排序】
冒泡排序就是把小的元素往前调(或者把大的元素往后调)。注意是相邻的两个元素进行比较,而且是否需要交换也发生在这两个元素之间。所以,如果两个元素相等,我想你是不会再无聊地把它们俩再交换一下。
如果两个相等的元素没有相邻,那么即使通过前面的两两交换把两个元素相邻起来,最终也不会交换它俩的位置,所以相同元素经过排序后顺序并没有改变。所以冒泡排序是一种稳定排序算法。
【选择排序】
选择排序是给每个位置选择当前元素最小的,比如给第一个位置选择最小的,在剩余元素里面给第二个元素选择第二小的,依次类推,直到第n - 1个元素,第n个元素不用选择了,因为只剩下它一个最大的元素了。那么,在一趟选择,如果当前元素比一个元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。比较拗口,举个例子,序列5 8 5 2 9,我们知道第一遍选择第1个元素5会和2交换,那么原序列中2个5的相对前后顺序就被破坏了。所以选择排序不是一个稳定的排序算法。
【插入排序】
插入排序是在一个已经有序的小序列的基础上,一次插入一个元素。当然,刚开始这个有序的小序列只有1个元素,就是第一个元素。比较是从有序序列的末尾开始,也就是想要插入的元素和已经有序的最大者开始比起,如果比它大则直接插入在其后面,否则一直往前找直到找到它该插入的位置。如果碰见一个和插入元素相等的,那么插入元素把想插入的元素放在相等元素的后面。所以,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序。所以插入排序是稳定的。
【快速排序】
在快速排序中,是随机选择一个数,然后小于它的放左边,等于它的放中间,大于它的放右边。默认快速排序是不稳定的。(其实快速排序可以做到稳定性问题,但是非常难,不需要掌握,可以搜“01 stable sort”)。
【归并排序】
归并排序是把序列递归地分成短序列,递归出口是短序列只有1个元素(认为直接有序)或者2个序列(1次比较和交换),然后把各个有序的短序列合并成一个有序的长序列,不断合并直到原序列全部排好序。可以发现,在1个或2个元素时,1个元素不会交换,2个元素如果大小相等也没有人故意交换,这不会破坏稳定性。那么,在短的有序序列合并的过程中,稳定是是否受到破坏?没有,合并过程中我们可以保证如果两个当前元素相等时,我们把处在前面的序列的元素保存在结果序列的前面,这样就保证了稳定性。所以,归并排序也是稳定的排序算法。
【堆排序】
我们知道堆的结构是节点i的孩子为2 * i和2 * i + 1节点,大顶堆要求父节点大于等于其2个子节点,小顶堆要求父节点小于等于其2个子节点。在一个长为n 的序列,堆排序的过程是从第n / 2开始和其子节点共3个值选择最大(大顶堆)或者最小(小顶堆),这3个元素之间的选择当然不会破坏稳定性。但当为n / 2 - 1, n / 2 - 2, ... 1这些个父节点选择元素时,就会破坏稳定性。有可能第n / 2个父节点交换把后面一个元素交换过去了,而第n / 2 - 1个父节点把后面一个相同的元素没 有交换,那么这2个相同的元素之间的稳定性就被破坏了。
举个简单的例子,假如有个数组4,4,4,5,5,在建立大顶堆的时候,第二个4会和第一个5的顺序调换,这样元素4的稳定性就被破坏了。所以,堆排序不是稳定的排序算法。

八、工程中的综合排序算法
假如有一个大数组,如果这个数组的长度很长,在工程上综合排序会先进行一个判断:数组里面装的是基础类型(int、double、char...)还是自己定义的类。如果装的是基础类型,会选择快速排序;如果装的是自己定义的类型,比如一个student类,里面有分数和班级两个字段,你可能会按照student中的某一个字段来排序,这时候会给你用归并排序来排;
但是如果数组的长度很短时,不管数组里面装的是什么类型,综合排序都不会选择快速排序,也不会选择归并排序,而是直接用插入排序。为什么要用插入排序呢?因为插入排序的常数项极低,当数据量小于60时,直接用插入排序,虽然插入排序的时间复杂度是O(n²),但是在样本量极小的情况下,O(n²)的劣势表现不出来,反而插入排序的常数项很低,导致在小样本的情况下,插入排序会非常快。所以在整个数组的长度小于60的情况下,是直接用插入排序的。
在一个数组中,一开始它的长度可能很大,这时候就有分治行为:左边部分拿去递归,右边部分拿去递归。当你递归的部分一旦小于60,直接使用插排,当样本量大于60、很大的时候,才使用快排或归并的方式,用递归的方式化为子问题。原来快排或归并的递归终止条件是:当只剩1个数(L==R)的时候直接返回这个数。而在综合排序算法中,递归终止的条件就改为:L和R相差不到60,即L>R-60时,终止条件就是里面使用插入排序。
为什么如果数组装的是基础类型时使用快速排序,数组装的是自己定义的类时使用归并排序呢?这也取决于排序的稳定性。
因为基础类型不需要区分原始顺序,比如说一个数组里面全部放的是整型{3,3,1,5,4,3,2},排完序后我们并不需要区分这3个“3”的原始顺序是怎么样的,因为基础类型,相同值无差异。快速排序是不稳定的。
而如果是自定义的类,比如一个student类,如果我们需要将student先按照分数排序,再按照班级排序,此时,相同班级的个体是不一样的,是有差别的,所以要用归并排序,因为归并排序是稳定的。
参考:https://www.cnblogs.com/shen-hua/p/5422676.html
https://www.cnblogs.com/asis/p/6798779.html
https://www.cnblogs.com/chengxiao/p/6194356.html
https://www.cnblogs.com/pipipi/p/9460249.html
https://blog.csdn.net/u010452388/article/details/81218540
https://blog.csdn.net/u013384984/article/details/79496052











 浙公网安备 33010602011771号
浙公网安备 33010602011771号