证明欧几里得算法的正确性

欧几里得算法又叫辗转相除法，是求解最大公约数的一种古老的方法。 

废话不多说，直接开证：

 　　题目：求解正整数a，b(a >= b)的最大公约数。

　　 a总可以用b来表示：a = qb + p;

　　 这个式子怎么理解呢？

　　我们可以这样理解：a是被除数，b是除数，q是商，p是余数(p = a % b)。

　　设 r 为a，b的最大公约数。

　　则a，b能被r整除(废话- _ -)。

　　下面重点来了：

　　　   　 

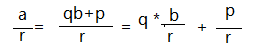
　　　　上式成立。

　　　　又因为q*b/r为整除，a也为整数

　　　　所以p/r也为整数，即 p 能被 r 整除

　　　　

　　　　此时 r 也是b, p的最大公约数。为什么呢？可以用反证法来简单证明

　　　　　　　假设存在一个更大的R(R > r) 能整除 b 与 p 

  　　　　　　 那么 R 就是a，b的最大公约数了，与 r 是a,b的最大公约数矛盾。

　　　　于是gcd(a,b) = gcd(b,p) = gcd(b,a%b)

　　　　递归求解就可以了。gcd函数的第二个参数为0时，第一个参数就是a,b的最大公约数。这里需要注意下，gcd()函数

　　　　的第一个参数要大于等于大二个参数。