博客作业四--树
1.学习总结(2分)
1.1树结构思维导图

1.2 树结构学习体会
理解:树是一种重要的非线性数据结构,其定义是递归的,所以递归的调用是树中是很重要的,若要使用非递归,则需要借助栈,队列等其他数据结构
树的一些概率能理解,但不会解决代码问题,尤其通过递归求后缀表达式,实在是很难。pta的题目很多都不会做。
2.PTA实验作业(4分)
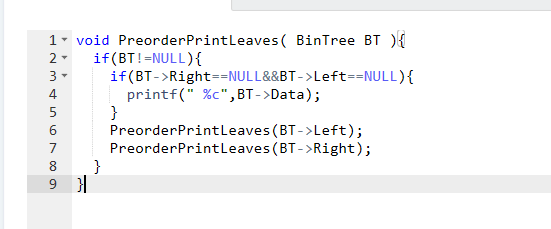
题目1:6-3 先序输出叶结点
设计思路(伪代码或流程图)
void PreorderPrintLeaves( BinTree BT )//先序输出叶结点
先序序列根,左,右
如果传下来根节点不为空
if(左右子树都不存在即为叶节点)输出叶节点
if(根存在)访问左子树,若存在继续递归访问左子树
访问右子树 ,若存在继续递归访问右子树
代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
PTA提交列表说明。

忽略空树的判断
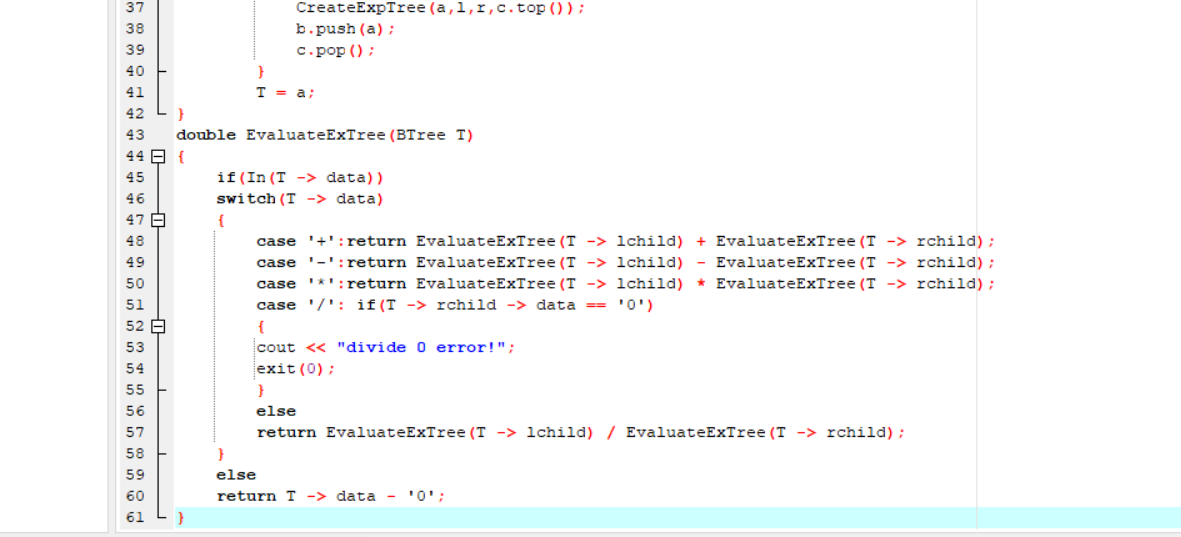
题目2:6-4 jmu-ds-表达式树
设计思路(伪代码或流程图)
void InitExpTree(BTree &T,string str) ; //建表达式的二叉树
定义栈 b存储数字,字符型栈 c 存储运算符
‘#’入栈c;
while( 字符串不空)
if (str[i] 为数字)
创建树节点,赋予str[i]的值,并置其左右孩子为空后再次入栈b;
else
调用Precede函数
case ‘<' 运算符入栈c;
case '=' c栈顶元素出栈
case '>' 创建新的树节点并赋予c栈顶元素值,右左孩子分别取b栈顶元素后再次入b栈;
while (栈c中仍有运算符)
创建新的树节点并赋予c栈顶元素值,右左孩子分别取b栈顶元素后再次入b栈;
double EvaluateExTree(BTree T);//计算表达式树
利用递归求值
while (树节点存在)
case '+' 返回 EvaluateExTree(T -> lchild) + EvaluateExTree(T -> rchild);
case '-' 返回EvaluateExTree(T -> lchild) - EvaluateExTree(T -> rchild);
case '*' 返回EvaluateExTree(T -> lchild) * EvaluateExTree(T -> rchild);
case '/'
if(b不为0) 返回EvaluateExTree(T -> lchild) / EvaluateExTree(T -> rchild);
代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)

PTA提交列表说明。

建树的代码不够规范,栈的用法也不够了解
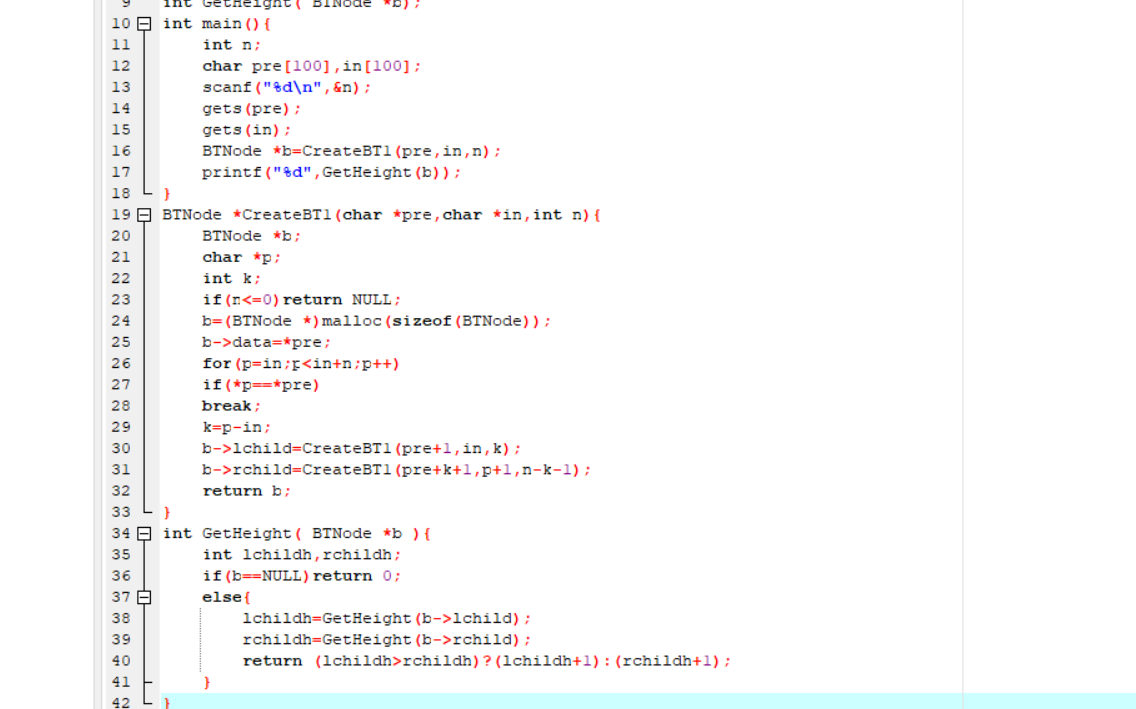
题目3:7-1 还原二叉树
设计思路(伪代码或流程图)
BinTree CreateTree(char *pre,char *in,int n)
{
BinTree T;
*p存放中序,
k用于标记先序序列的值
*pre在中序序列中位置
n<=0 return NULL;
b申请空间,b->data=*pre;
for p=in to in+n 在中序中查找*pre所在的位置k.
}
int GetHeight(BinTree T)
{
.递归构造左右子树.
if(b==NULL)return 0;
lchildh=GetHeight(b->lchild);
rchildh=GetHeight(b->rchild);
递归求出高度max
return max;
}
代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
PTA提交列表说明。

3.截图本周题目集的PTA最后排名(3分)
3.1 PTA排名

3.2 我的得分:1.5
4. 阅读代码
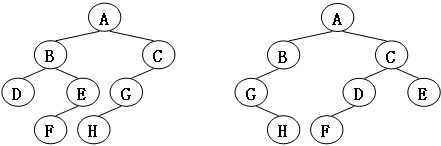
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。
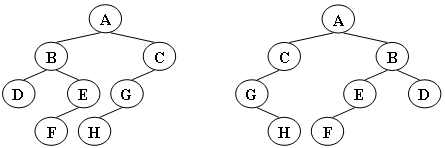
现给定两棵树,请你判断它们是否是同构的。
输入格式:
输入给出2棵二叉树树的信息。对于每棵树,首先在一行中给出一个非负整数NN (\le 10≤10),即该树的结点数(此时假设结点从0到N-1N−1编号);随后NN行,第ii行对应编号第ii个结点,给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空,则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意:题目保证每个结点中存储的字母是不同的。
输出格式:
如果两棵树是同构的,输出“Yes”,否则输出“No”。
输入样例1(对应图1):
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
输出样例1:
Yes
输入样例2(对应图2):
8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4
输出样例2:
No
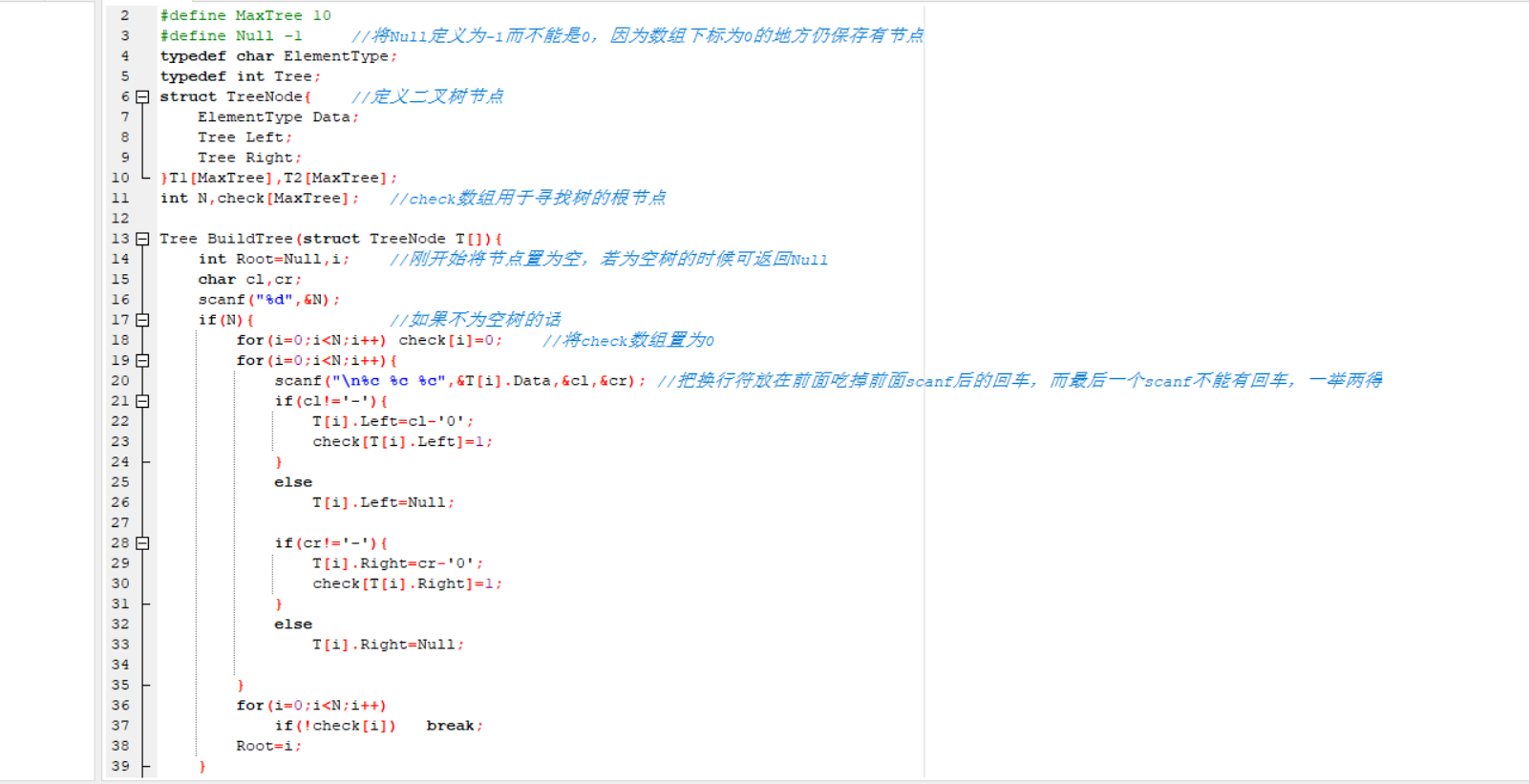

思路:我们考虑用静态链表的方式也就是数组存储树简单一点,因为此题节点与节点之间是有下标关系的,输入的顺序就是节点的编号,某个节点的保存了左右子树的下标,所以可以通过下标访问数组的方式得到它的左右子树。还有一个需要解决的问题就是我们判断两棵树是否同构,首先要找到它的根节点才能进行下面的比较,从输入的数据以及图中可以发现根节点是没有节点指向它的,所以我们用check数组保存所有节点的指向(下标)置为0,每次从输入中获取到指向后,将指向的数组位置置为1,最后没有被指到的位置的节点即为根节点。


