D1. Toy Train (Simplified)

D1. Toy Train (Simplified)

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

This is a simplified version of the task Toy Train. These two versions differ only in the constraints. Hacks for this version are disabled.

Alice received a set of Toy Train™ from Bob. It consists of one train and a connected railway network of nn stations, enumerated from 11through nn. The train occupies one station at a time and travels around the network of stations in a circular manner. More precisely, the immediate station that the train will visit after station ii is station i+1i+1 if 1≤i<n1≤i<n or station 11 if i=ni=n. It takes the train 11 second to travel to its next station as described.

Bob gave Alice a fun task before he left: to deliver mm candies that are initially at some stations to their independent destinations using the train. The candies are enumerated from 11 through mm. Candy ii (1≤i≤m1≤i≤m), now at station aiai, should be delivered to station bibi (ai≠biai≠bi).

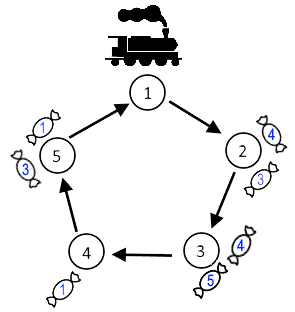The blue numbers on the candies correspond to bibi values. The image corresponds to the 11-st example.

The train has infinite capacity, and it is possible to load off any number of candies at a station. However, only at most one candy can be loaded from a station onto the train before it leaves the station. You can choose any candy at this station. The time it takes to move the candies is negligible.

Now, Alice wonders how much time is needed for the train to deliver all candies. Your task is to find, for each station, the minimum time the train would need to deliver all the candies were it to start from there.

Input

The first line contains two space-separated integers nn and mm (2≤n≤1002≤n≤100; 1≤m≤2001≤m≤200) — the number of stations and the number of candies, respectively.

The ii-th of the following mm lines contains two space-separated integers aiai and bibi (1≤ai,bi≤n1≤ai,bi≤n; ai≠biai≠bi) — the station that initially contains candy ii and the destination station of the candy, respectively.

Output

In the first and only line, print nn space-separated integers, the ii-th of which is the minimum time, in seconds, the train would need to deliver all the candies were it to start from station ii.

Examples

input

Copy

5 7
2 4
5 1
2 3
3 4
4 1
5 3
3 5

output

Copy

10 9 10 10 9 

input

Copy

2 3
1 2
1 2
1 2

output

Copy

5 6 

Note

Consider the second sample.

If the train started at station 11, the optimal strategy is as follows.

1. Load the first candy onto the train.
2. Proceed to station 22. This step takes 11 second.
3. Deliver the first candy.
4. Proceed to station 11. This step takes 11 second.
5. Load the second candy onto the train.
6. Proceed to station 22. This step takes 11 second.
7. Deliver the second candy.
8. Proceed to station 11. This step takes 11 second.
9. Load the third candy onto the train.
10. Proceed to station 22. This step takes 11 second.
11. Deliver the third candy.

Hence, the train needs 55 seconds to complete the tasks.

If the train were to start at station 22, however, it would need to move to station 11 before it could load the first candy, which would take one additional second. Thus, the answer in this scenario is 5+1=65+1=6 seconds.