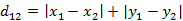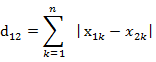[机器学习系列] k-近邻算法（K–nearest neighbors）

C++ with Machine Learning -K–nearest neighbors

我本想写C++与人工智能，可是转念一想。人工智能范围太大了，我根本介绍不完也没能力介绍完，所以还是取了他的子集。我想这应该是一个有关机器学习的系列文章，我会不定期更新文章，希望喜欢机器学习的朋友不宁赐教。

本系列特别之处是与一些实例相结合来系统的解说有关机器学习的各种算法。因为能力和时间有限，不会向诸如Simon Haykin<<NEURAL NETWORKS>>等大块头具体的解说某一个领域的全部算法与概念。我会有选择的解说一些算法作为引导。假设要继续深入则推荐读者系统阅读相关书籍。

首先你须要做的事情就是放松，不要被一大堆字吓到，由于他们都很浅显易懂，我相信认真看的每一个人都能明确K近邻算法。

K–nearest neighbors,简称 KNN/kNN,用来处理分类和回归，它是最简单的Machine Learning Algorithm。所以以它为开端。

这里考虑一个实例。有两个小组AB，A组为实践组，B组为理论组，A组的实践分平均为90，理论为30，B组实践分为20分，理论分为70分，如今有一个同学实践60分。理论60分，她究竟属于哪个组？

就像上面的图片一样，只是我们能够使用欧氏距离[附录]计算出未知点与其它四个点的距离（相似度/相似值），然后把计算出来的值从小到大排序。选择K个值（这就是k的由来），这K个值都是选择最小的。

比方最后用欧氏距离计算出来的距离是

与1点的距离：5,

与2点的距离：5.3

与3点的距离：2.2

与4点的距离：7.12

我们就须要对上面排序，排成这样：

与3点的距离：2.2

与1点的距离：5,

与2点的距离：5.3

与4点的距离：7.12

整理一下上面的思路：

1）读取训练样本集（这里我用x0y0和type三个数组分别保存每一个数据的第一个特征值第二个特征值和类型）

2）读取须要分类的数据，然后计算须要分类的数据和训练样本集中每一个数据的距离（计算出来的数据须要用map之类的容器与类型关联）

3）把上面计算的每一个距离排序（map排序）

4）如果是从上到下升序。那就从上选择k个值

5）统计这k个之中哪个类型出现频率最高，最高的就是分类结果

这里如果K=3。就意味这我们须要选择前面三个数据，然后推断前面三个数据中A和B。3点是B类。1点是A类。2点是B类。这里显然B类多一些。所以未知数就是B类。到这里算法是想就解释了，非常easy把，由于它是最简单的ML算法，以下就是C++的实现了

//A bad version about k-nearest neighbour algorithm,just a teaching sample.
#include <iostream>
#include <algorithm>
#include <map>
#include <math.h>

const int k=3;

std::ostream & operator<<(std::ostream& out, const std::pair<double,char>& p) {
  return out << p.first << "\t" << p.second;
}
//训练样本数据集
class simple_data{
public:
    simple_data(double x,double y,char classtype):
        type(classtype),datx(x),daty(y)
    {}
    inline double get_distance(double x0,double y0){
        return sqrt((pow(datx-x0,2)+pow(daty-y0,2)));//欧氏距离
    }
    char type;
private:
    double datx;
    double daty;
};


int main(){
    //构造<span style="font-family: Arial, Helvetica, sans-serif;">训练样本数据集，这样正常情况下应该从文本读入。
为了方便就直接构造了</span>
    simple_data sd1(1.0,2.0,'A');
    simple_data sd2(2.0,3.0,'A');
    simple_data sd3(12.0,13.0,'B');
    simple_data sd4(8.0,9.0,'B');

    //读入须要分类的新数据，并计算它和全部点的距离
    double newdata[2]={1.0,1.0};
    std::map<double,char> mp;
    mp.insert(std::pair<double,char>(sd1.get_distance(newdata[0],newdata[1]),sd1.type));
    mp.insert(std::pair<double,char>(sd2.get_distance(newdata[0],newdata[1]),sd2.type));
    mp.insert(std::pair<double,char>(sd3.get_distance(newdata[0],newdata[1]),sd3.type));
    mp.insert(std::pair<double,char>(sd4.get_distance(newdata[0],newdata[1]),sd4.type));
    //得到类似度，并进行排序，最后输出
    unsigned int acout=0,bcout=0,i=0;
    std::cout<<"类似度："<<'\t'<<"类型:\n";
    for(std::map<double,char>::iterator iter = mp.begin();
         iter != mp.end();++iter)
    {
        i++;
        std::cout << *iter <<std::endl;
        if(i<k){
            if(mp[i]='A'){
                acout++;
            }else{
                bcout++;
            }
        }
    }
    if(acout>bcout)
        std::cout<<"未知类型数属于：A";
    else
        std::cout<<"未知类型数属于：B"

}

这是一个比較糟糕的版本号。比方样本数据直接指定了（通常是从其它文件读入）。只是目的非常easy就是这样能省去一些读写文件的代码能看得清楚一些。

这里我写了一个拙劣的KNN API：https://github.com/racaljk/MachineLearning

有待改进的地方还有非常多，我会陆续完好它。

补充

假设要计算2个以上特征值须要注意的除了改变距离计算方法之外还要注意K值尽量不要太大，实际上这一rule也存在于两个特征值，K值的大小和和数据的准确度是影响计算的两个方面，又尤其是数据准确度。建议尽量三位小数内进行计算。由于最后我们的目的是分类不是精确计算。

附：

1)欧氏距离

最常见的两点之间或多点之间的距离表示法，又称之为欧几里得度量，它定义于欧几里得空间中，如点 x = (x1,...,xn) 和 y = (y1,...,yn) 之间的距离为：