hdu 4865 Peter's Hobby (隐马尔可夫模型 dp)
Peter's Hobby
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 292 Accepted Submission(s): 132
Problem Description
Recently, Peter likes to measure the humidity of leaves. He recorded a leaf humidity every day. There are four types of leaves wetness: Dry , Dryish , Damp and Soggy. As we know, the humidity of leaves is affected by the weather.
And there are only three kinds of weather: Sunny, Cloudy and Rainy.For example, under Sunny conditions, the possibility of leaves are dry is 0.6.
Give you the possibility list of weather to the humidity of leaves.
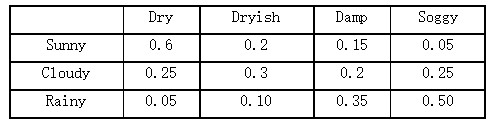
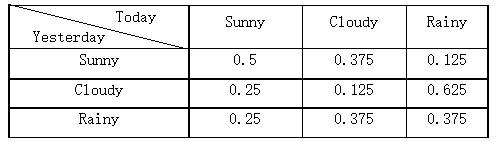
The weather today is affected by the weather yesterday. For example, if yesterday is Sunny, the possibility of today cloudy is 0.375.
The relationship between weather today and weather yesterday is following by table:
Now,Peter has some recodes of the humidity of leaves in N days.And we know the weather conditons on the first day : the probability of sunny is 0.63,the probability of cloudy is 0.17,the probability of rainny is 0.2.Could you know the weathers of these days most probably like in order?
Give you the possibility list of weather to the humidity of leaves.

The weather today is affected by the weather yesterday. For example, if yesterday is Sunny, the possibility of today cloudy is 0.375.
The relationship between weather today and weather yesterday is following by table:

Now,Peter has some recodes of the humidity of leaves in N days.And we know the weather conditons on the first day : the probability of sunny is 0.63,the probability of cloudy is 0.17,the probability of rainny is 0.2.Could you know the weathers of these days most probably like in order?
Input
The first line is T, means the number of cases, then the followings are T cases. for each case:
The first line is a integer n(n<=50),means the number of days, and the next n lines, each line is a string shows the humidity of leaves (Dry, Dryish, Damp, Soggy)
The first line is a integer n(n<=50),means the number of days, and the next n lines, each line is a string shows the humidity of leaves (Dry, Dryish, Damp, Soggy)
Output
For each test case, print the case number on its own line. Then is the most possible weather sequence.( We guarantee that the data has a unique solution)
Sample Input
1 3 Dry Damp Soggy
Sample Output
Case #1: Sunny Cloudy RainyHintLog is useful.
题意:
真难解释清楚。给你一个海藻的状态序列,让你找出一个最有可能的天气序列。前一天的天气能影响今天的天气,海藻的状态受天气的影响。
(从题目中应该是读不出他是如何影响的。详细看以下的推荐的链接)
思路:
这事实上是隐马尔可夫模型(HMM)的一个应用,依据可观察状态的序列找到一个最可能的隐藏状态序列,隐马尔可夫模型介绍见这里:点击打开链接
dp[i][j]表示第i天天气为j的概率。dp[i][j]=dp[i-1][k]*wea[k][j]*lea[j][num[i]],记录路径,最后输出最有可能的路径。依据最后一天的概率来看。
代码1:(不用log的代码)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <string>
#include <map>
#include <stack>
#include <vector>
#include <set>
#include <queue>
#define maxn 105
#define MAXN 100005
#define mod 1000000009
#define INF 0x3f3f3f3f
#define pi acos(-1.0)
#define eps 1e-10
typedef long long ll;
using namespace std;
int n,m,flag,cnt,tot,test=0;
int num[55],pre[55][4];
double dp[55][4];
char s[50];
double lea[3][4]=
{
{0.6, 0.2, 0.15, 0.05},
{0.25, 0.3, 0.2, 0.25},
{0.05, 0.10, 0.35, 0.50}
};
double wea[3][3]=
{
{0.5, 0.375, 0.125},
{0.25, 0.125, 0.625},
{0.25, 0.375, 0.375}
};
char res[3][15]=
{
"Sunny","Cloudy","Rainy"
};
void output(int x,int y)
{
if(x==0) return ;
output(x-1,pre[x][y]);
printf("%s\n",res[y]);
}
void solve()
{
int i,j,k,t,id;
double ma,tmp;
dp[1][0]=0.63*lea[0][num[1]];
dp[1][1]=0.17*lea[1][num[1]];
dp[1][2]=0.2*lea[2][num[1]];
for(i=2;i<=n;i++)
{
for(j=0;j<3;j++)
{
ma=-1;
for(k=0;k<3;k++)
{
tmp=dp[i-1][k]*wea[k][j]*lea[j][num[i]];
if(ma<tmp)
{
ma=tmp; id=k;
}
}
dp[i][j]=ma; pre[i][j]=id;
}
}
ma=-1;
for(j=0;j<3;j++)
{
if(dp[n][j]>ma)
{
ma=dp[n][j]; id=j;
}
}
printf("Case #%d:\n",++test);
output(n,id);
}
int main()
{
int i,j,t;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
for(i=1;i<=n;i++)
{
scanf("%s",s);
if(strcmp(s,"Dry")==0) num[i]=0;
else if(strcmp(s,"Dryish")==0) num[i]=1;
else if(strcmp(s,"Damp")==0) num[i]=2;
else num[i]=3;
}
solve();
}
return 0;
}
代码2:(乘法多了之后损失精度,能够用log)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <string>
#include <map>
#include <stack>
#include <vector>
#include <set>
#include <queue>
#define maxn 105
#define MAXN 100005
#define mod 1000000009
#define INF 0x3f3f3f3f
#define pi acos(-1.0)
#define eps 1e-10
typedef long long ll;
using namespace std;
int n,m,flag,cnt,tot,test=0;
int num[55],pre[55][4];
double dp[55][4];
char s[50];
double lea[3][4]=
{
{0.6, 0.2, 0.15, 0.05},
{0.25, 0.3, 0.2, 0.25},
{0.05, 0.10, 0.35, 0.50}
};
double wea[3][3]=
{
{0.5, 0.375, 0.125},
{0.25, 0.125, 0.625},
{0.25, 0.375, 0.375}
};
char res[3][15]=
{
"Sunny","Cloudy","Rainy"
};
void output(int x,int y)
{
if(x==0) return ;
output(x-1,pre[x][y]);
printf("%s\n",res[y]);
}
void solve()
{
int i,j,k,t,id;
double ma,tmp;
dp[1][0]=log(0.63)+lea[0][num[1]];
dp[1][1]=log(0.17)+lea[1][num[1]];
dp[1][2]=log(0.2)+lea[2][num[1]];
for(i=2;i<=n;i++)
{
for(j=0;j<3;j++)
{
ma=-INF;
for(k=0;k<3;k++)
{
tmp=dp[i-1][k]+wea[k][j]+lea[j][num[i]];
if(ma<tmp)
{
ma=tmp; id=k;
}
}
dp[i][j]=ma; pre[i][j]=id;
}
}
ma=-INF;
for(j=0;j<3;j++)
{
if(dp[n][j]>ma)
{
ma=dp[n][j];
id=j;
}
}
printf("Case #%d:\n",++test);
output(n,id);
}
int main()
{
int i,j,t;
for(i=0;i<3;i++)
{
for(j=0;j<4;j++)
{
lea[i][j]=log(lea[i][j]);
if(j<3) wea[i][j]=log(wea[i][j]);
}
}
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
for(i=1;i<=n;i++)
{
scanf("%s",s);
if(strcmp(s,"Dry")==0) num[i]=0;
else if(strcmp(s,"Dryish")==0) num[i]=1;
else if(strcmp(s,"Damp")==0) num[i]=2;
else num[i]=3;
}
solve();
}
return 0;
}




