剑指offer_39_数组中出现次数超过一半的数字

数组中出现次数超过一半的数字

题目链接：https://leetcode-cn.com/problems/shu-zu-zhong-chu-xian-ci-shu-chao-guo-yi-ban-de-shu-zi-lcof/

题目内容：数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1:

输入: [1, 2, 3, 2, 2, 2, 5, 4, 2]
输出: 2

题目解析

题目解析内容来自于题解中Krahets 和评论网友

题目的意思是简单明了的，给定一个数组，这个数组里面有一个数字出现此处超过数组总个数的一半。找到这个数。

方法一：python 导包

from collections import Counter

class Solution:
    def majorityElement(self, nums):
        res = Counter(nums)  // 获取的是 Counter 类
        return res.most_common(1)[0][0]  // most_common 列出前 n 个 元素 

Counter 可参考此。此方法时间复杂度，空间复杂度待补充

方法二：手动实现哈希表，即 python 字典

自己手动实习一个 python 字典。记录每个字符的数量，当统计某个字符的数量超过字符总数的一半，即可直接返回。

class Solution:
    def majorityElement(self, nums):
        if not nums:
            return None
        
        num_dict = dict()
        max_count, max_num = len(nums), nums[0]
        
        for num in nums:
            if num in num_dict:
                num_dict[num] += 1
            else:
                num_dict[num] = 1
            
            if num_dict[num] > max_count:
                max_count = num_dict[num]
                max_num = num
        return max_num

复杂度分析

• 时间复杂度：O(N)
• 空间复杂度：O(N)

方法三：数组排序法

将数组排序，由于众数的特性，即本题目中众数的数量超过总数量的一半，因此 数组中要求的数字一定是众数，且其在排序后的数组中一定在数组的中间

class Solution:
    def majorityElement(self, nums):
        if not nums:
            return
        sorted(nums)
        return nums[len(nums)//2]

复杂度分析

• 时间复杂度：O(Nlog2N)

方法四：摩尔投票法

核心理念为"正负抵消；是本题的最佳解法

解释：

• 票数和：由于众数出现的参数超过数组长度的一半；若记 众数 的票数为 +1 ，非众数 的票数为 -1 ，则一定有所有数字的 票数和 > 0 。

• 票数正负抵消： 设数组 nums 中的众数为 x ，数组长度为 n 。若 nums 的前 a 个数字的 票数和 = 0 ，则 数组后 (n-a)个数字的 票数和一定仍 >0 （即后 (n−a) 个数字的 众数仍为 x

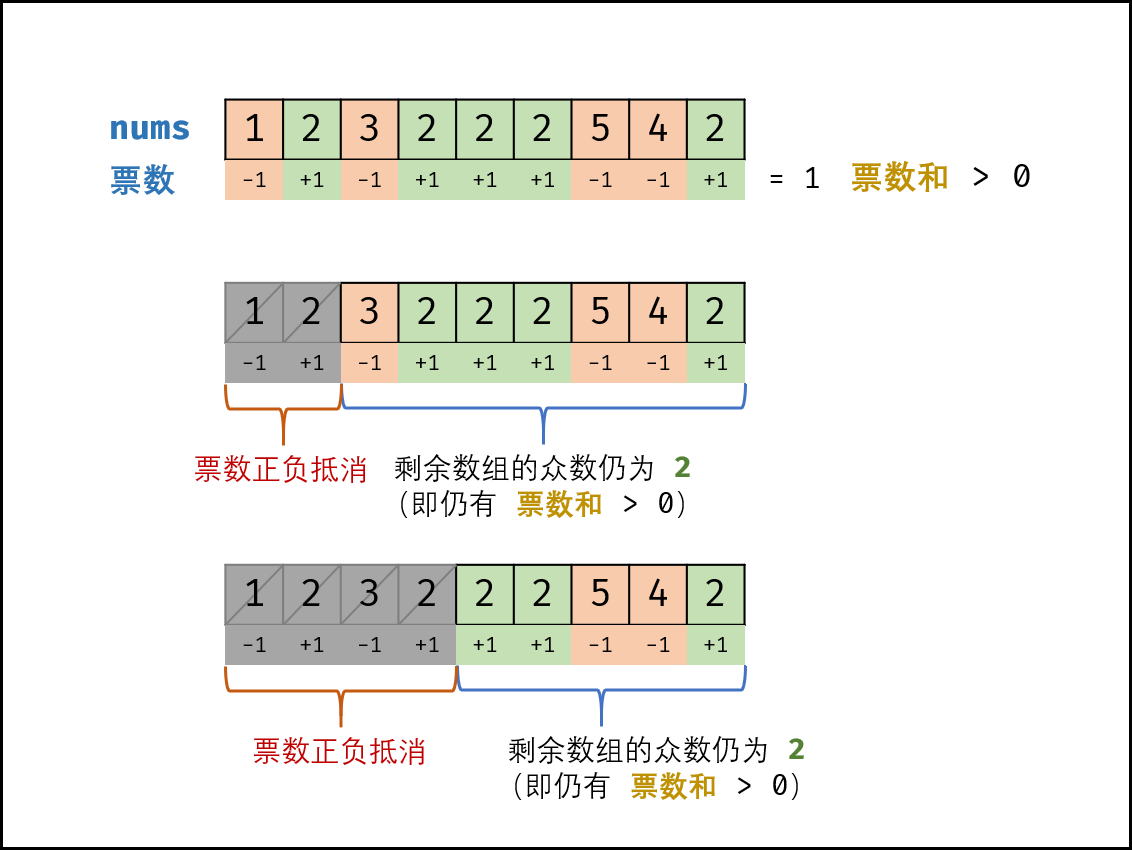
算法原理：

• 为构建正负抵消，假设数组首个元素 n_1为众数，遍历统计票数，当发生正负抵消时，剩余数组的众数一定不变 ，这是因为（设真正的众数为 x ）：
  • 当 n_1 =x ： 抵消的所有数字中，有一半是众数 xx 。
  • 当 n_1 \neq = x ： 抵消的所有数字中，少于或等于一半是众数 x 。
• 利用此特性，每轮假设都可以 缩小剩余数组区间 。当遍历完成时，最后一轮假设的数字即为众数（由于众数超过一半，最后一轮的票数和必为正数）。

算法流程

1. 初始化： 票数统计 votes = 0， 众数为 x

2. 循环抵消：遍历数组 nums 中的每个数字 num;

   1. 当票数 votes 等于 0，即假设当前数字 num 为众数 x；
   2. 当 num = x 时，票数 votes 自增 1； 否则，票数 votes 自减 1

3. 返回值：返回众数 x 即可

复杂度分析：

• 时间复杂度 O(N) ： N 为数组 nums 长度。
• 空间复杂度 O(1) ： votes 变量使用常数大小的额外空间。

class Solution:
    def majorityElement(self, nums):
        votes = 0
        for num in nums:
            if votes == 0:
                x = num
            votes += 1 if num == x else -1
        return x

题目拓展：

• 由于题目明确给定 给定的数组总是存在多数元素，因此本题不考虑 数组中不存在众数的情况

• 若考虑这种情况，需要在代码逻辑中加入一个 ”验证“，遍历数组中 已经求得的 x 的数量。

  • 若 x 的数量超过数组长度的一半，则返回 x
  • 否则，返回 0

• 时间复杂度仍为 O(N), 空间复杂度仍为 O(1)

class Solution:
    def majorityElement(self, nums):
        votes, count = 0, 0
        for num in nums:
            if votes == 0:
                x = num
            votes += 1 if num == x else -1
        
        # 验证 x 是否为众数
        for num in nums:
            if num == x:
                count += 1
        return x if count > len(nums) // 2 else 0   # 当无众数时返回 0