剑指offer_38_字符串的全排列
字符串的全排列
题目链接:https://leetcode-cn.com/problems/zi-fu-chuan-de-pai-lie-lcof/
题目描述:输入一个字符串,打印出该字符串中字符的所有排列。你可以以任意顺序返回这个字符串数组,但里面不能有重复元素。
示例:
输入:s = "abc"
输出:["abc","acb","bac","bca","cab","cba"]
限制:1 <= s 的长度 <= 8
题目解析
题目解析内容参考自题解中krahets
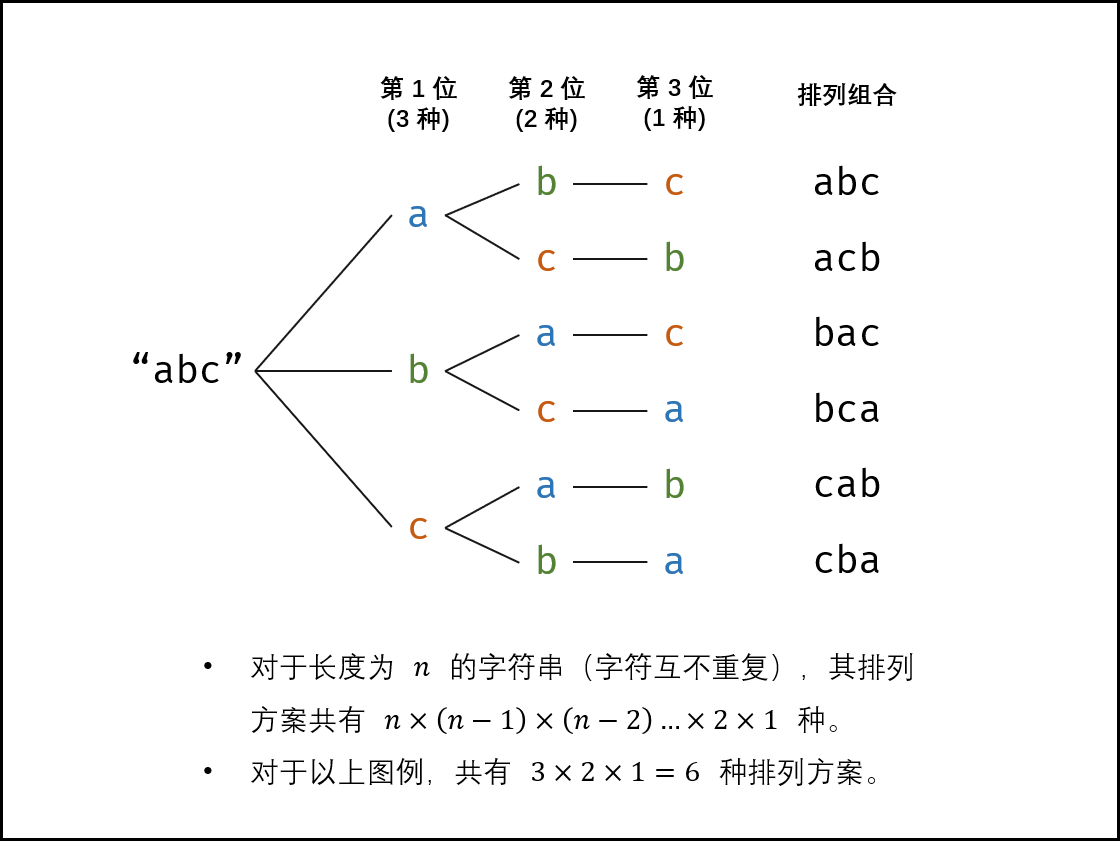
排列方案的数量:全排列,对于一个长度为 n 的字符串(假设字符互不重复),其排列共有 n * (n - 1) * (n - 2) ... * 2 * 1 种方案
排列方案的生成方法:根据字符串排列的特点,可将字符串分为两部分。
- 首字母
- 首字母之后的字母
选中第一个字母后,将剩下的字母仍按照上述进行拆分。由此,可以得出一个递归的思想。
根据上述流程可以采用深度优先搜索的方式。见下图。
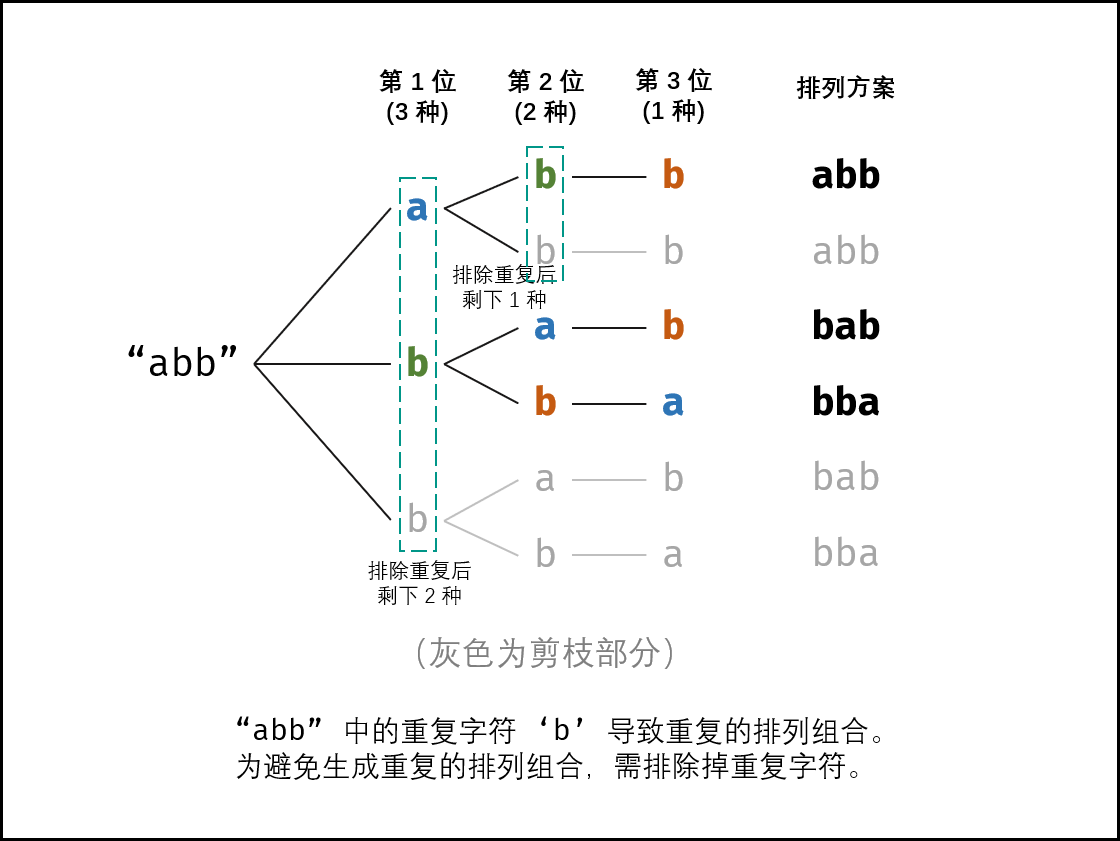
重复方案与剪枝: 当字符串存在重复字符时,排列方案中也存在重复方案。为排除重复方案,需在固定某位字符时,保证 “每种字符只在此位固定一次” ,即遇到重复字符时不交换,直接跳过。从 DFS 角度看,此操作称为 “剪枝” 。
递归解析:
- 终止条件: 当 x = len(c) - 1 时,代表所有位已固定(最后一位只有 1 种情况),则将当前组合
c转化为字符串并加入res,并返回; - 递推参数: 当前固定位
x; - 递推工作: 初始化一个 Set ,用于排除重复的字符;将第 x 位字符与 i∈[x,len(c)] 字符分别交换,并进入下层递归;
- 剪枝: 若 c[i] 在 Set 中,代表其是重复字符,因此“剪枝”;
- 将 c[i] 加入 Set ,以便之后遇到重复字符时剪枝;
- 固定字符: 将字符 c[i] 和 c[x] 交换,即固定 c[i] 为当前位字符;
- 开启下层递归: 调用 dfs(x + 1) ,即开始固定第 x + 1 个字符;
- 还原交换: 将字符 c[i] 和 c[x] 交换(还原之前的交换);
以上总结就是一句话,在已经变成列表的字符串,调换各个参数的位置,从而达到,不同排序的列表。
复杂度分析:
- 时间复杂度 O(N!) : N 为字符串 s 的长度;时间复杂度和字符串排列的方案数成线性关系,方案数为N×(N−1)×(N−2)…×2×1 ,因此复杂度为 O(N!) 。
- 空间复杂度 O(N^2): 全排列的递归深度为 N ,系统累计使用栈空间大小为 O(N) ;递归中辅助 Set 累计存储的字符数量最多为 N + (N-1) + ... + 2 + 1 = (N+1)N/2 ,即占用 O(N^2)的额外空间。
代码
class Solution:
def permutation(self, s: str) -> List[str]:
c, res = list(s), []
def dfs(x):
if x == len(c) - 1:
res.append(''.join(c)) # 添加排列方案
return
dic = set()
for i in range(x, len(c)):
if c[i] in dic: continue # 重复,因此剪枝
dic.add(c[i])
c[i], c[x] = c[x], c[i] # 交换,将 c[i] 固定在第 x 位
dfs(x + 1) # 开启固定第 x + 1 位字符
c[i], c[x] = c[x], c[i] # 恢复交换
dfs(0)
return res


