剑指offer_36_二叉搜索树与双向链表
二叉搜索树与双向链表
题目链接:https://leetcode-cn.com/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof/
题目描述:输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
为了让您更好地理解问题,以下面的二叉搜索树为例:
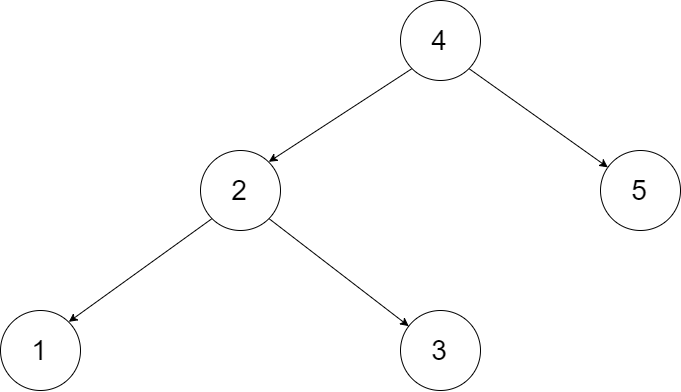
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。
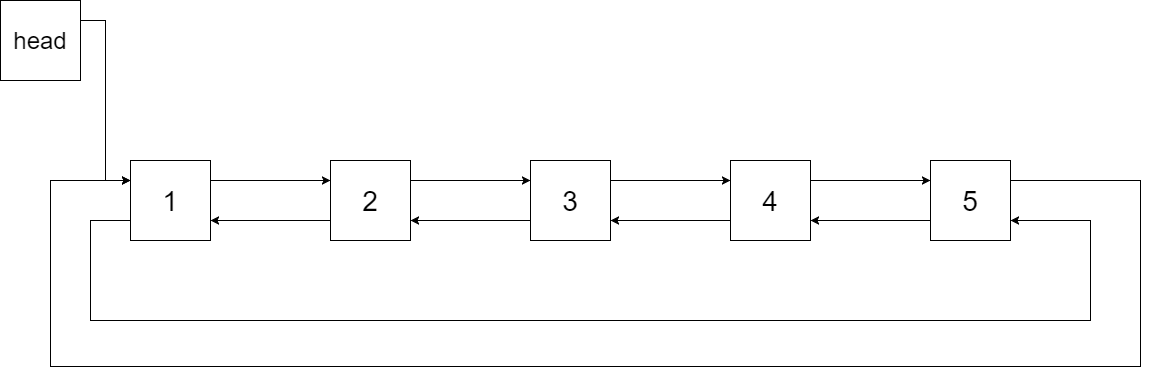
特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
题目解析
题目解析内容来自于题解中Krahets
题目的意思还是很明确的。基于二叉搜索树的性质,我们使用中序遍历可得到二叉搜索树的递增序列
将 二叉搜索树 转换成一个 排序的循环双线链表 ,其中包含三个要素:
- 排序链表:节点应该从小到大排序,因此应使用 中序遍历 从小到大 访问数节点;
- 双向链表:在构建相邻节点(设前驱节点 pre,当前节点 cur )关系时,不仅应 pre.right = cur, cur.left = pre。
- 循环链表:设链表头结点 head 和尾结点 tail , 则应构建 head.left = tail 和 tail.right = head。
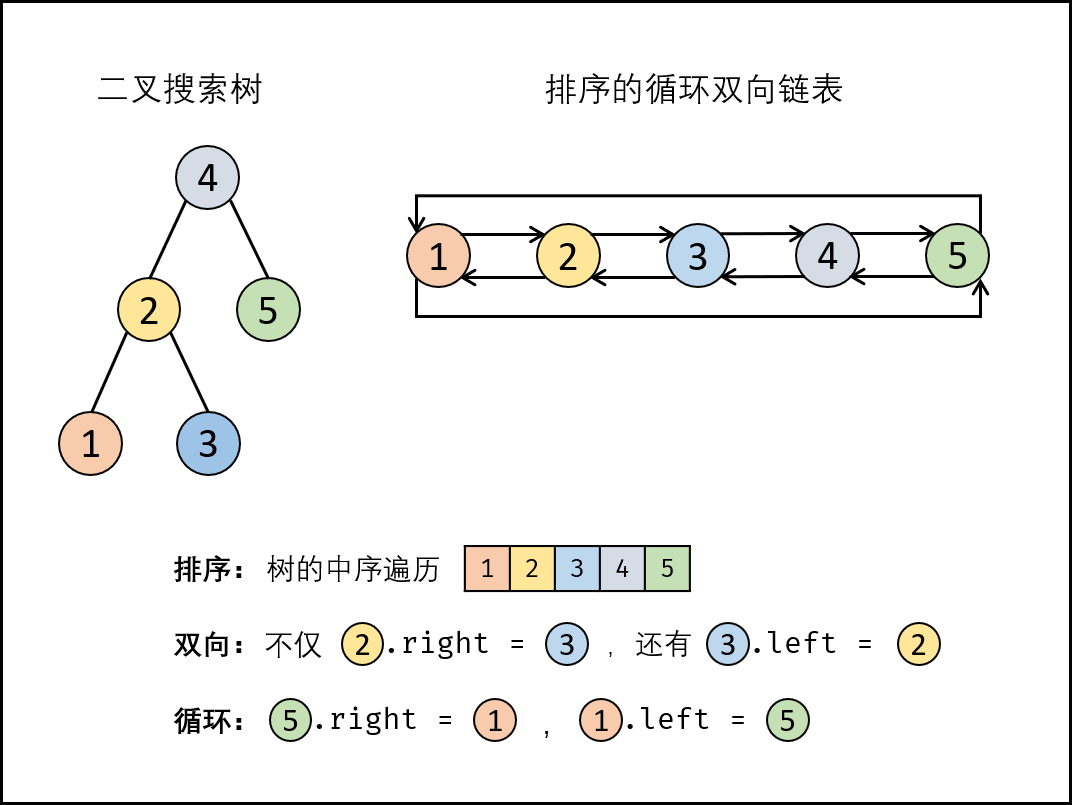
中序遍历 为 “左 根 右” 顺序,递归实现代码如下:
# 中序遍历
def in_traversal(root):
ret = []
def traversal(root):
if not root:
return
traversal(root.left)
ret.append(root.val)
traversal(root.right)
traversal(root)
return ret
根据以上分析,考虑使用中序遍历访问树的各节点 cur ;并在访问每个节点时构建 cur 和前驱节点 pre 的引用指向;中序遍历完成后,最后构建头节点和尾节点的引用指向即可。
算法流程
in_traversal(cur): 递归法中序遍历
-
终止条件:当节点
cur为空时,代表已经越过叶子节点,此时可直接返回 -
递归左子树,即
in_traversal(cur.left) -
构建链表:
- 当
pre为空时:代表当前访问的是链表的头结点,记为head
2. 当pre不为空时:修改双向节点引用,即pre.right = cur,cur.left = pre;
3. 保存cur:更新pre = cur, 即节点cur是后继节点的pre
- 当
-
递归右子树,即
in_traversal(cur.right)
treeToDoublyList(root):
- 特例处理:若节点
root为空,则直接返回; - 初始化:空节点
pre - 转化为双向链表:调用
in_traversal(root); - 构建循环链表:中序遍历完成后,
head指向头节点,pre指向尾结点,因此修改head和pre的双向节点引用即可 - 返回值:返回链表的头节点
head即可
复杂度分析
- 时间复杂度:O(N)
- 空间复杂度:O(N)
代码
class Solution:
def treeToDoublyList(self, root: 'Node') -> 'Node':
def in_traversal(cur):
if not cur:
return
in_traversal(cur.left) # 递归左子树
if self.pre: # 修改节点引用
self.pre.right, cur.left = cur, self.pre
else: # 记录头节点
self.head = cur
self.pre = cur # 保存 cur 当前节点变成 pre
in_traversal(cur.right) # 递归右子树
if not root:
return
self.pre = None
in_traversal(root)
self.head.left, self.pre.right = self.pre, self.head
return self.head
附一个迭代版方法:
class Solution:
def treeToDoublyList(self, root: 'Node') -> 'Node':
if not root:
return
stack = []
pre = None
while stack or root:
if root:
stack.append(root)
root = root.left
else:
node = stack.pop()
if not pre:
head = node
else:
pre.right = node
node.left = pre
pre = node
root = node.right
head.left, node.right = node, head
return head


