后缀树论文笔记
原文献链接
本文所有思路全为原文献思路,只是做了解读
后缀\(Trie\)的一些定义:
\(T\) :字符串
\(\sum\) :字符集,即\(T\)中的字符组成的集合
\(Q\) :后缀树的状态集合
\(\overline{x}\) :表示后缀\(x\)的状态
\(g\): 转换函数,\(g(\overline{x},a)=\overline{y}\)表示的是\(y=xa\),\((a ∈ Σ)\)
\(f\) :后缀链接,定义为对于一个非空后缀\(x\),若有\(x=ay\)\((a ∈ Σ)\),则\(f(\overline{x})=\overline{y}\)
\(⊥\): 辅助状态,对应于空字符串,\(f(root)=⊥\),而对于任意的\((a ∈ Σ)\),有\(g(⊥,a)=root\)
\(F\): 最终状态
有了上述定义,则一棵字符串\(T\)的后缀树可以定义为:
\(ST rie(T ) =\)(Q ∪ \(\{⊥\},\) $root, F, g, f $)
下图为后缀链接的演示,此树为后缀\(Trie\)而非后缀树:
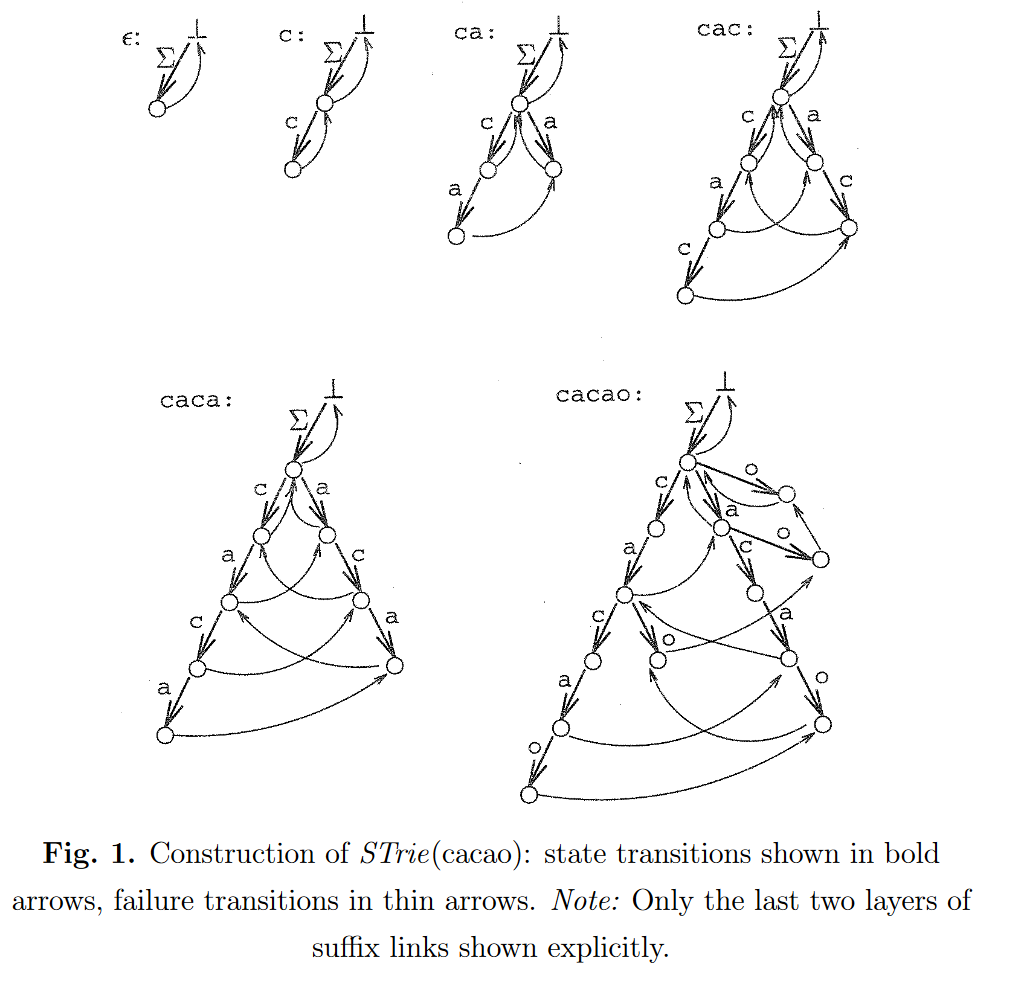
建立上树会耗费很多时间,由于节点太多,它的复杂度会达到\(O(T^2)\)
后缀树
一些观察:
\(T[1,n]\)的后缀可由\(T[1,n-1]\)的后缀加上\(s[n]\),以及一个空串得到
后缀链接会形成几条路径,最后指向\(⊥\),把这种路径称为边界路径
为了减少节点数,原本\(Trie\)树上每一条边相当于一个字符,现在改为一个字符串,也就是将很多条边压缩为一条边,中间的点数也就少了下来,因此转移函数也变为\(g(\overline{s},w)=\overline{r}\) ,其中\(w\)为一字符串,而一般我们不这样表示,而是\(g(\overline{s},(k,p))\)表示,原先的\(w\)用\(T[k,p]\)代替
因此从此处开始,上文的定义中代表字符的,现在会代表字符串,也就是定义会稍作改变
减少了节点数,必然造成中间过程中有很多节点没有显现出来,直到后面才新建插入,我们把这类节点称为隐式节点,已经存在的称为显式节点,那么隐式节点的状态可有二元组表示\(r=(s,w)\),其中\(r\)表示隐式状态,\(s\)表示隐式状态\(r\)在后缀树上的祖先,\(w\)为两个状态之间的转移字符串,若\(s\)取最近祖先,也意味着\(w\)尽可能短,则称之为\(canonize\),在此也使用两个指针\(k,p\)表示\(w\),对于显式状态,记为\(s=(s,\epsilon)\),其中\(\epsilon\)表示空字符,用二元组表示字符串则为:\(s=(s,(p+1,p))\)
论文中还提出了两类节点,一个是活动点,一个是结束点
活动点具有两个性质:
1、比活动点更长的后缀都是叶子节点,边每次都会要扩展
2、活动点后加入的后缀都不是叶子结点
所以我们每次开始更新只需要从活动点开始更新,因为比活动点更长的后缀已经是叶子节点了,可以不需要再管了,结构不会再变化了
而结束点则是每次扩展到哪个点就可以停止的那个点.当我们扩展后缀树,沿着边界路径遍历时,如果当前状态\(\overline{z}\),存在一个转换\(g(\overline{x},t_i)=\overline{zt_i}\),那么我们不需要继续遍历下去,因为原来的树必定包括\(zt_i\)的所有后缀,我们不妨把首个这样的节点定义为结束点。比结束节点长的后缀必然是叶节点,这一点很好解释,要么本来就是叶节点,要么就是新创建的节点(新创建的必然是叶节点)。这意味着,每一个前缀更新完之后,当前的结束点将成为下一轮更新的活动点.
同时,由于巧妙地定义,对于\(T_{i-1}\)的后缀树,\(s_1=t_1t_2\cdots t_{i-1}\)一定是叶子节点,因此活动点一定存在。
而对于任意的\((a ∈ Σ)\),有\(g(⊥,a)=root\),因此对于\(⊥\)而言,永远满足结束点的定义。所以活动点和结束点永远存在
从而每次更新只需要在活动点和结束点之间更新即可
下如图为建立\(cacao\)的后缀树的过程
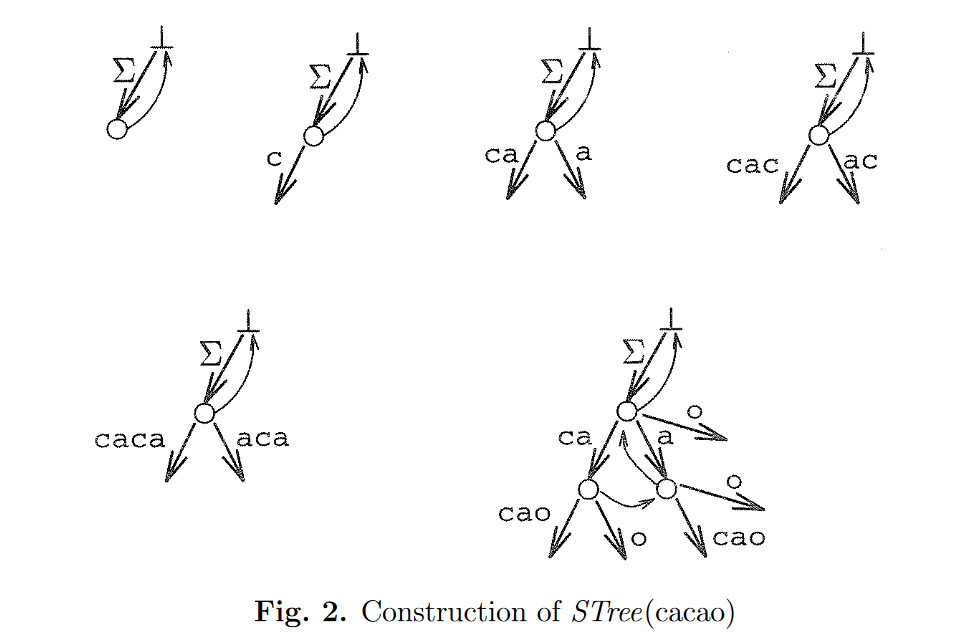
通过观察,发现以下引理:
记\(s_j\)为每轮活动点,\(s_j'\)为每轮结束点\((j\le j')\)
每次扩展会对\(1\le h<j'\)的相关信息进行修改,具体分为两种:
对于\(1\le h < j\) 这些叶子节点,新扩展的那个字符产生的转换会影响这些原本存在的边,使其代表的字符串增加\(t_i\)这个字符
对于\(j\le h< j'\)这些节点,会新增加一条边
对于第一种修改,我们不需要找到每个通向叶子结点的转换,并且扩张它们的右端点,我们只需要把连向叶子结点的转换,定义为生长转换,对于生长转换,它的右端点始终为当前总字符串的长度,于是对于这些点不需要进行实质性的更新
而对于第二种修改则有点棘手,我们会发现这些状态可能是隐式状态,藏在某条边上,令\(h=j\),找到它的最近的显式节点,则\(s_h=(s,w)\),其中\(w\)为\(T_{i-1}\)的后缀,即\(s_h=(s,(k,i-1))\),如果\(j==j'\)直接退出,否则查看\((s,(k,i-1))\)这个节点是否为显式节点,如果不是,则新建一个节点,此时\(s_h\)有显式节点表示了,需要做的是新增一个转换,注意到新增的转换会是生长转换\(g′(s_h,(i, ∞)) = s′_h\),因为\(s'_h\)会是一个新的叶子节点,另外,如果是分裂边产生的\(s'_h\),则\(f(s'_h)\)需要更新,然后继续更新下一个后缀\(s_{h+1}\),参考\(s_h=(s,(k,i-1))\),知道\(s_{h+1}=(f(s),(k',i-1))\)。
同理更新\(s_{h+2}\)一直到找到\(j'\)为止
通过上述算法得到伪代码:





