浅谈"$fake$树"——虚树
树形$dp$利器——"$fake$"树(虚树$qwq$)
前置知识:
$1、$$dfs$序
$2、$倍增法或者树链剖分求$lca$
问题引入:
在许多的树形动规中,很多时候点特别多,而又有一些毒瘤操作,导致很多时候,原本优秀的算法变得很鸡肋,而虚树就是解决这种问题的一把利器
那让我们来看一道例题:
一句话题意:给定一棵$n$个节点的树,$m$次询问,每次给出几个点,要你删除若干条边使得这些点不和根节点联通
我们看到数据范围:
$n<=2e5,\sum k<=5e5$
考虑朴素的$dp$,状态和方程都很好想,大概就是:
对于一个点,可以删除它到根节点的边的最小值,或者是把子树中连向标记点的链中最小的边删除(当然还要考虑当前点是不是标记点等因素,不过这不是重点$qwq$)
那么一次询问就是$O(n)$,看上去确实很优秀了,但是有$m(m<=5e5)$次询问,那么总时间复杂度就是$O(nm)$的算法了,$m$大一点就会炸得飞起,然而其实每一次我们都遍历了每一个节点,但其实只需要遍历我们需要的关键点就行了,我们看到$\sum k<=5e5$,这也就告诉了我们,如果总的时间复杂度跟$\sum k$有关的话,就可以通过,而虚树则可以帮助我们把询问点等关键点提取出来,那么总共就只需要遍历少许关键点,最后的时间复杂度就跟$\sum k$有关啦
什么是虚树?
在我的理解下,其实就是从原有的树中,把需要的关键节点和边提取出来后组成的新树,就叫虚树
虚树上的点一般有被询问的点,以及它们互相的$lca$和根节点 ,而边则存的是最小值,最大值,边权和等,视情况而定。
那么根据上面的题意,我们就可以用虚树剔除对结果无意义的点,避免过多的重复计算,从而降低时间复杂度
虚树的构建:
我们维护一个栈,维护的是一条以栈顶元素为端点的一条链(最右链)
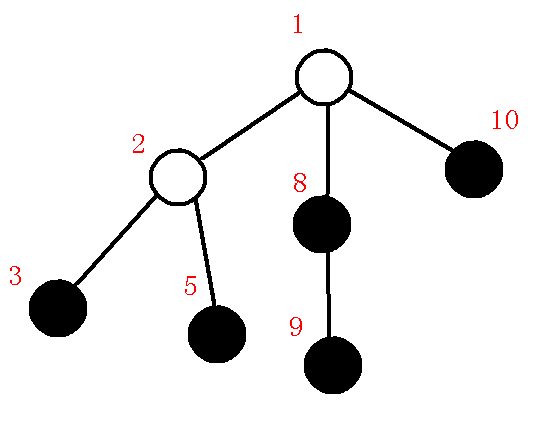
首先,先把整棵树$dfs$一遍,求出每个节点的$dfs$序,顺便求出深度,举个例子,假如原树为:
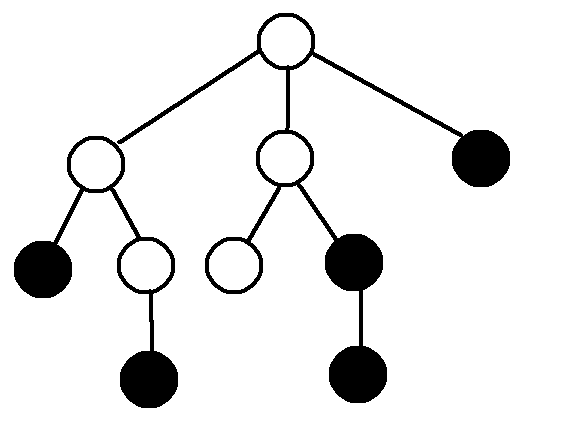
其中黑色点为询问点,那么我们先把深度和$dfs$序求出来,如下图:
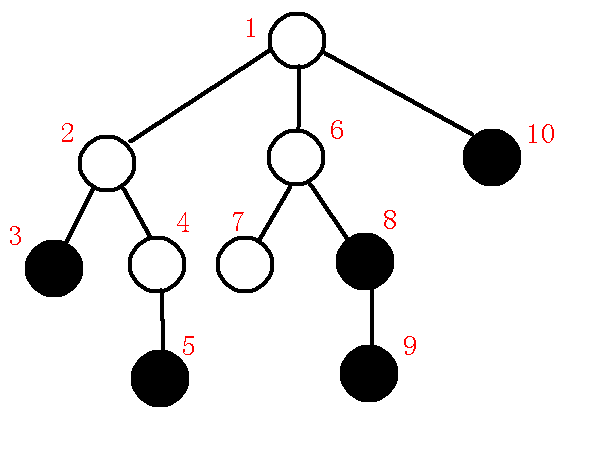
红色数字是$dfs$序,深度的话肉眼看就行了,怕图片有点混乱就省略了
一开始呢,我们求出$dfs$序后,把所有关键点按照$dfs$从小到大排序
具体做法(如果不懂请跟着后文图解一起思考):
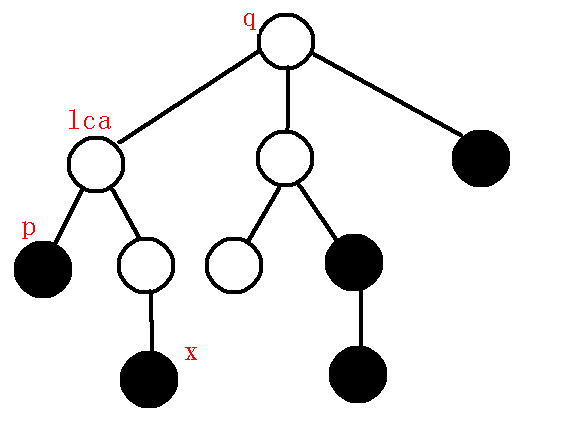
假设栈顶元素为$p$,而要插入的关键节点为$x$,求出它们的$lca$,那么会有下列两种情况:
$1、$$lca$是$p$:如下图:
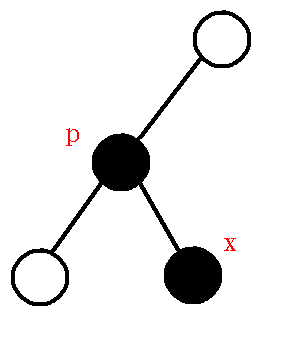
$2、$$p,x$分别位于$lca$的两棵子树上,如下图:

你可能会问, 那么为什么没有$lca$是$x$的情况呢?
我们思考:我们 遍历的顺序是按照$dfs$序来的,那么设对于每个点$i$的$dfs$序为$dfn[i]$,那么会有$dfn[p]<dfn[x]$,但是如果$lca$是$x$的话,$x$的$dfs$序肯定小于$p$点的,互相矛盾,所以不成立
那么对于上面第一种情况,我们直接将$x$点入栈即可,为什么呢?
我们思考$lca==p$的情况告诉了我们什么信息:
它告诉我们我们本来维护的是(下文数字都是图中$dfs$序)$1-2$这条链,而现在我们要把$4$维护进去,然而因为$lca==p$,我们发现我们可以直接维护$1-2-4$这条链,所以直接压栈即可
例如压栈后,栈内($dfs$序)情况如下:
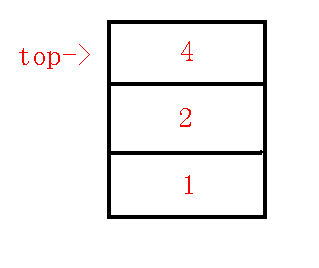
就是在维护下图中红色这条链(根节点一开始就在栈内):
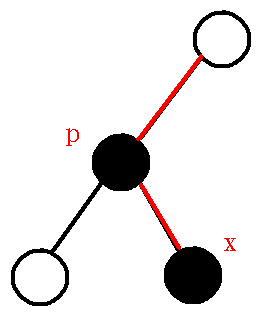
而对于第二种情况,就比较复杂了,我们设栈顶第二个元素为$q$,那么我们循环判断下面$3$种小情况讨论:
$1、$$dfn[q]>dfn[lca]$:什么意思呢?我们先画一幅图:
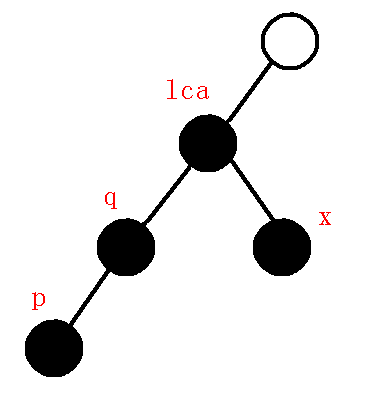
那么这幅图告诉了我们什么信息呢:
以$q$为根的子树已经遍历完毕,现在进入到了以$x$为根的子树,现在需要把以$q$为根的子树的信息存好
那么在遍历到$p$点时,我们栈中维护的是什么呢?很明显栈内元素($dfs$序)为:

那么也就是维护了从$1-2-3-4$这条树链,也就是说我本来维护的是下图的链:
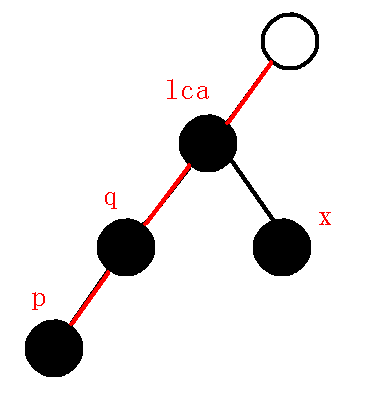
而现在我们需要维护下图的链:
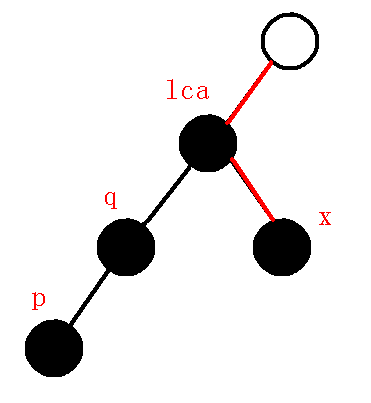
那显然我们要退栈把$p$弹出去,那么就失去了$q-p$的信息,所以我们要在虚树上连边,把要失去的信息保存下来,也就是把$q-p$在虚树上连边,退栈一次,再循环
所以,当$dfn[q]>dfn[lca]$时,由$q$向$p$在虚树上连边,并且退一次栈
$2、$$dfn[q]=dfn[lca]$:那么我们接着上幅图,退一次栈后如下图(紫色边为在虚树上已连接的边):
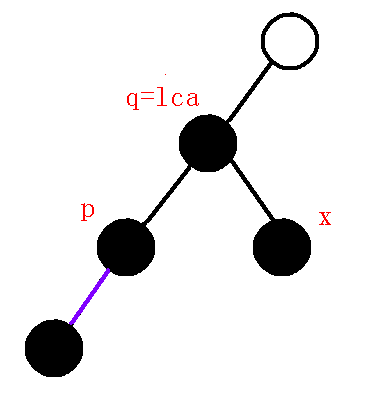
那么我们发现我们只需要连接$lca-p$的边就可以维护好左子树了,那么连完边后,就要维护右子树的链,所以把$x$压入栈中
所以当$dfn[q]==dfn[lca]$时,由$lca$或者$q$向$p$连边,并且把$x$节点压栈,终止循环
$3、$$dfn[q]<dfn[lca]$时:这个就比较有意思了,我们需要重新画一幅图:

首先,栈顶元素就是$p$,第二个元素是$q$(根节点一开始就在栈内),然而我们发现$dfn[q]<dfn[lca]$,也就是说$lca$被$p,q$夹在中间了,那么我们同样思考这代表了什么?
$1、$$p$与$lca$之间没有关键点了,因为最近的关键点为$q$,这也就告诉我们$lca$的左子树就差$lca-p$这一条边了,所以我们要再退一次栈,并且虚树上连边$lca-p$
$2、$$lca$不在栈中,也就是说$lca$不是询问点,但是它是关键点,因为它连接着$p,x$的关系等,所以它是不可忽略的,所以我们如果要维护到$x$的链的话,就必须把$lca$也加入栈中
所以,当$dfn[q]<dfn[lca]$时,虚树上连边$lca-p$,退栈,把$lca,x$按顺序压栈,终止循环
最后要注意的是,栈内还会有元素没有退出,所以最后还要把栈内元素依次连边
上面就是建虚树的过程了,如果还是不懂,可以配合下文一起理解,多多回味,其实很好理解的
图解虚树建立过程:
对于一开始的图,我们模拟它虚树的建立过程,初始图:
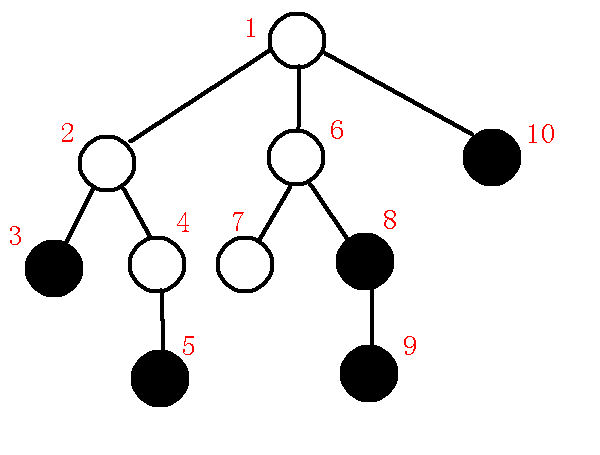
$1、$插入根节点
我们首先要维护的肯定是根节点了,那么我们把根节点入栈:
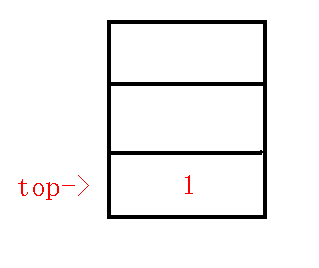
$2、$插入$3$节点
把询问点按照$dfs$序排列后,下一个待插入的点为$3$,那么 我们求出$lca(1,3)$,其实就是$1$节点,那么也就满足最上面的第一种情况$lca==p$,所以直接压栈,维护$1-3$这条链,此时栈内情况:
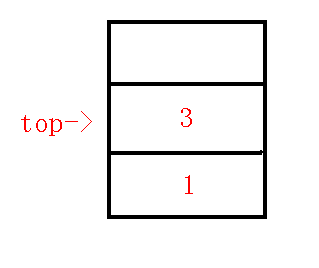
$3、$插入$5$节点
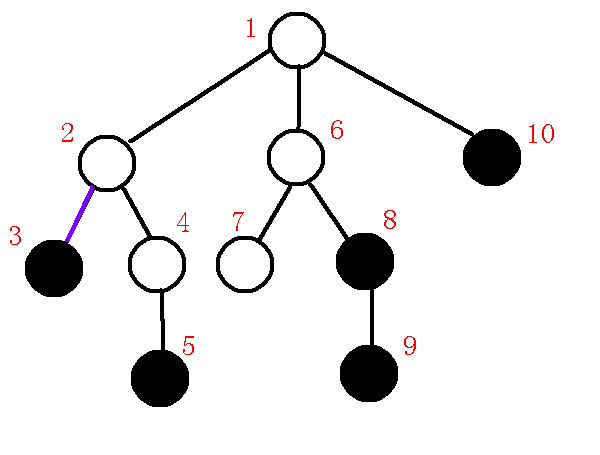
下一个询问点为$5$节点,那么求出栈顶元素$3$与$5$的$lca$为$2$,发现,$p,x$位于不同子树,所以求出$q$为$1$,也就是下图:
我们发现$dfn[q]<dfn[lca]$,那么也就是说我们只需要连接$lca-p$就可以维护完成左子树了,(具体说明见上文),所以我们在虚树上连边$lca-p$,退栈,把$lca,x$压入栈中,那么也就是说本来维护的是$1-3$这条链,而现在改成维护$1-2-5$这条链了,那么树中栈中情况如下:
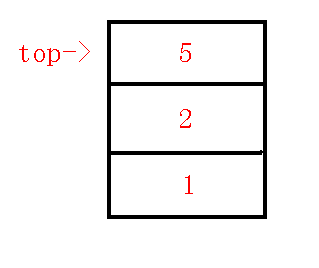
$4、$插入$8$节点
我们还是像原来一样,求出$5,8$的$lca$为$1$,那么我们求出$q$为$2$,发现$dfn[q]>dfn[lca]$也就是说$q$还在$lca$的原来遍历的子树中,那么现在$x$很明显在一个新的子树,栈内需要维护新的链,那么原来的链就要在虚树上保存下来,所以我们连接$q-p$,退栈,发现$q$变成了$1$,$p$变成了$2$,此时$dfn[q]=dfn[lca]$,那么也就是满足第二种情况,也就是告诉我们只需要连接的$lca-$这条边后这个子树就遍历完了,所以我们连边$lca-p$,退栈,把$x$压栈,维护新的链$1-8$,终止循环,完成后如下图:
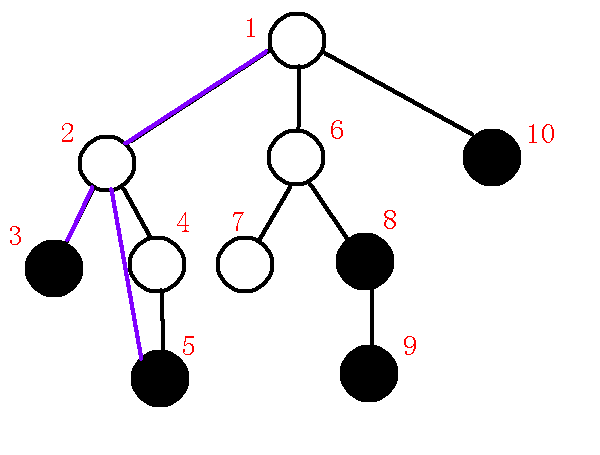
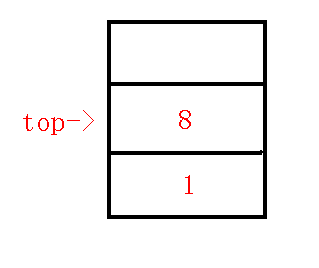
$5、$插入$9$节点
我们还是按照以往一样,求出$9,8$的$lca$为$8$,也就是$lca(p,x)=p$的情况,这时候说明在一条链上,可以直接压栈维护,所以直接把$9$压栈,此时维护的链为$1-8-9$,栈内情况:

$6、$插入$10$节点
求出$10,9$的$lca$为$1$,那么发现在不同子树中,求出$q$为$8$,那么发现$dfn[q]>dfn[lca]$,那么把$q-p$连边,(为什么上文已经提及),然后退栈,此时$p=8,q=1,lca=1$,发现$dfn[q]=dfn[lca]$,所以连边$lca-p$,退栈,把$10$压栈,如下图:
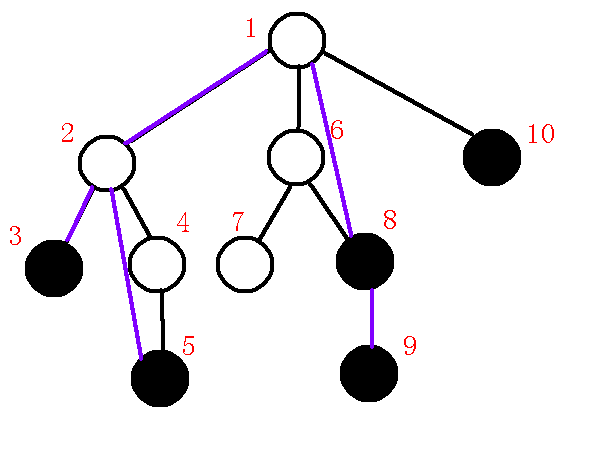
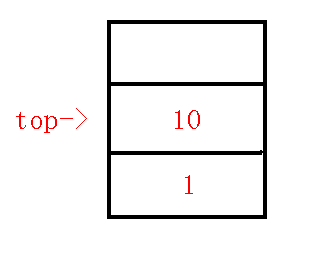
$7、$清空栈内剩余元素
我们依次由$stack[top-1]$向$stack[top]$连边,也就是连接$1-10$,完成后如下:
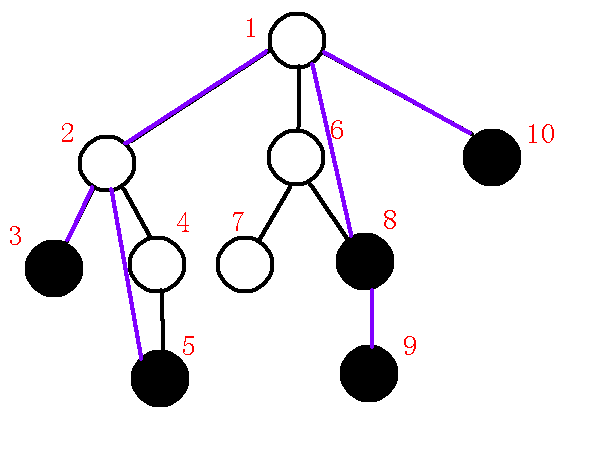
那么到这里,虚树就建完了,把紫色的边提出来就是虚树了,也就是下图:
代码实现:
void Build(int x)
{
stack[++top]=1;
for(int i=0;i<mark.size();++i)
{
int x=mark[i];
int lca=Lca(x,stack[top]);
if(lca==stack[top])
{
stack[++top]=x;
return ;
}
while(top>1&&dfn[stack[top-1]]>=dfn[lca])
Add(stack[top-1],stack[top]),--top;
if(lca!=stack[top])
Add(lca,stack[top]),stack[top]=lca;
stack[++top]=x;
}
}
尾声:
如果本篇博客有问题,请联系我
如果觉得有帮助,不要吝啬你的赞$qwq$


 浙公网安备 33010602011771号
浙公网安备 33010602011771号