强势图解回文自动机
题外话:
本文为博主原创文章,转载请附上博文链接!https://www.cnblogs.com/yexinqwq/p/10086668.html
其实回文自动机跟其他自动机差不太多吧,(特别是模板代码短)
如果有任何错误或着有更好的理解,请联系我!
前置知识:
1、马拉车算法(大概吧,其实个人认为不学也没关系)
2、
关于回文自动机:
回文自动机其实就是回文树,是由俄罗斯人于年夏发明的,然而关于回文自动机,其实它并不是严谨的树形结构,因为它有两棵子树,其中一颗节点编号为,它的子树是长度为偶数的回文串,并且这个节点长度设为,而另一棵子树编号为,它的子树是长度为奇数的回文串,特别的是:它的长度设置为!!!(至于为什么,因为它可以方便代码书写,以后会提到)
变量声明:
:普通的字典树
:指针,指向当前回文串的最长回文后缀,后面会详细介绍
:存放当前节点回文串的长度
:最新添加的回文节点
:总的节点个数
声明:
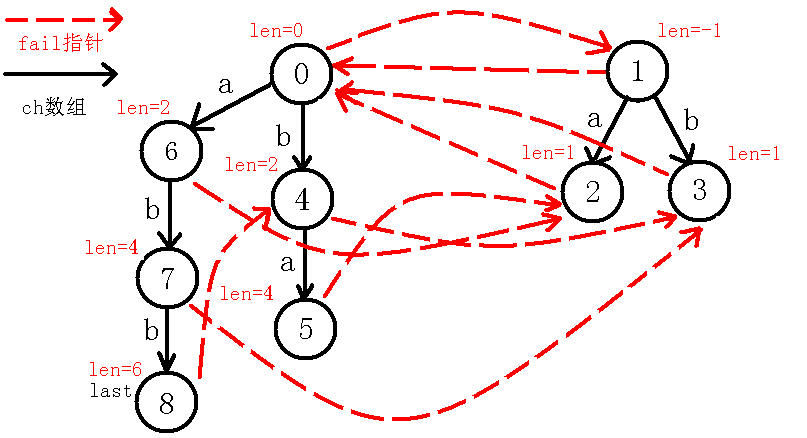
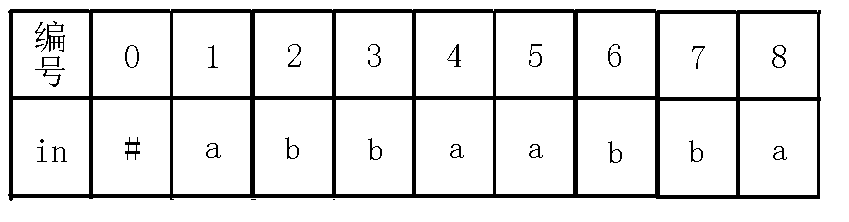
对于一个节点,我不称它为当前节点的编号!而是把每个节点当做一个回文串!例如abbaabba这个例子,完整的回文自动机如下(省略指针):
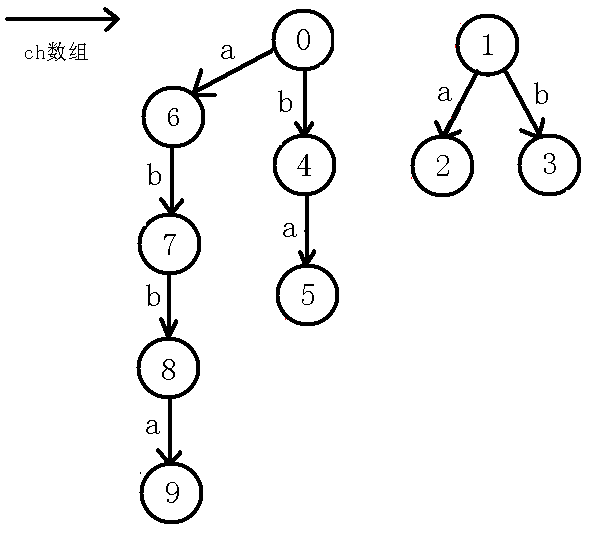
在上图中,我们对号节点不叫它号节点,而叫它abba,(请记住,因为后文这样便于理解),这样叫的原因是节点经过了的转移到了号节点,而就相当于在原来的基础上前后各增加了一个,即号节点叫做bb,同样,号节点经过的转移到了号节点,就在前后各加一个,即abba。但是需要注意的是,因为号节点为,而每次长度添加都添加个,所以这样就可以保证的子树中的长度都为奇数,这就是号节点为的好处,(如果是现在不懂没有关系,请跟着下面的图解一步一步思考!!!)
大概流程:
在图解之前,还是要让你们朦胧中有一丝印象,知道每步在干吗!(所以这里没看懂的话没关系,到了图解那里一起来理解!),建立回文自动机的过程如下:
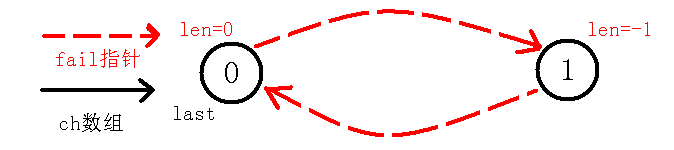
初始化:
'#'可以不是#,只要是不会出现的字符就行。
,
1、找到最新建立的节点,找到以结尾的最长回文串的开头的位置,如果和当前位置字符相同的话(假设当前字符为),说明在这个回文串的基础上两边都有字符,也就是说会有一个本质不同的回文串产生,否则跳指针,找到以点结尾的最长回文后缀(不包括自身),最终找到如果节点没有的转移,那么我们就让自增,即新建了一个节点,因为我们找到两边都是字符,所以新的回文节点长度为原来的
2、如果节点没有的转移,那么我们就让自增,即新建了一个节点,因为我们找到两边都是字符,所以新的回文节点长度为原来的,同时定义为,找到以当前节点的最长回文后缀,使指向它。
3、更新节点,继续插入下一个字符。
先贴代码,方便以后查看:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | scanf("%d",&n); scanf("%s",in+1); in[0]='#'; fail[0]=1;len[1]=-1;//初始化 for(int i=1;i<=n;i++) { int j; while(in[i-len[last]-1]!=in[i]) last=fail[last];//匹配(后面会详细解说) if(!ch[last][in[i]-'a'])//新建节点 { len[++cnt]=len[last]+2;//长度比原来多2 j=fail[last]; while(in[i-len[j]-1]!=in[i]) j=fail[j]; fail[cnt]=ch[j][in[i]-'a']; ch[last][in[i]-'a']=cnt; } last=ch[last][in[i]-'a']; } printf("%d",ans); |
如何构建指针以及为什么要这样构建:
回文自动机其实是找回文串的,那么怎么样才能找回文串呢?我们假设现在已插入的字符串为,而我们现在要插入
字符,我们用肉眼可以发现会是一个新的回文串,那么它是怎么构成的呢,我们可以发现它其实是原来的字符串的最长回文后缀两端各加上构成的,而为什么要找最长回文后缀呢?
1、为什么要最长:
那么我们思考,假如上面的的最长回文后缀我们不当做是,而是,那么它的两端都会是,也会构成一个回文串,但是!如果最长回文后缀是的话,两端匹配后,会出现这个回文串,并且!它的最长回文后缀就是,也就是说最长会保证每个回文串都在失配的情况被遍历,如果失配了,就继续找当前串的最长回文后缀(不包括自身)
2、为什么要回文:
其实这个问题很简单,如果中间不回文的话,就算两边字符相同,构成的新串也不会是回文的
3、为什么要后缀:
因为新的字符必须得跟以前插入的回文串相联系,如果是,而你要插入,如果你找的是最长的回文但不是后缀,那么其实是匹配不到的,因为它们没有联系。
强势图解开始!!!
首先我们初始化'#',,,也就是下图:
1、插入字符
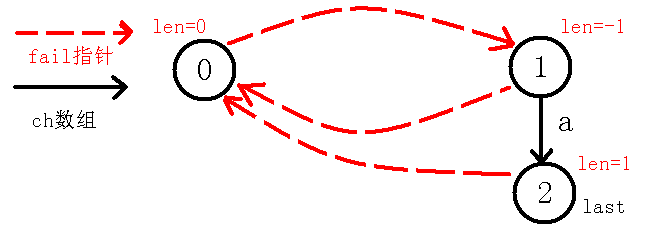
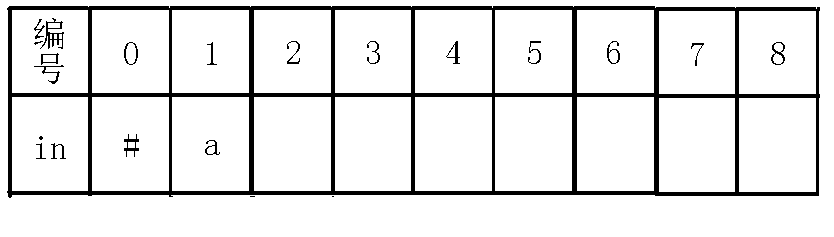
一开始为,而即,也就是说与不能构成回文串,那么我们就得缩小范围,就跳指针到节点,此时,也就是说,也就是自己等于自己,因为我们把回文串的范围由转为了,所以现在回文串的长度也就是,即也就是,所以这也是节点长度赋值为的好处,还保证了的子树长度为奇数。此时节点没有的转移,我们就连一条边向。即下图:
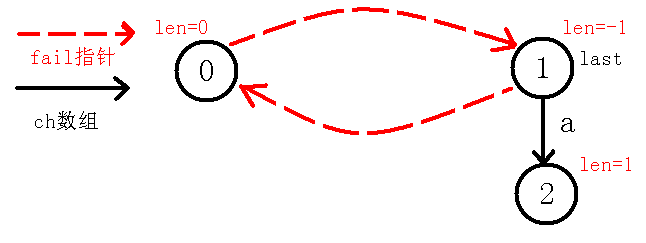

现在我们考虑求出节点(节点)的指针,我们要知道指针指向当前节点的最长回文后缀(不包括自己),我们可以看到当前节点就是,没有不包括自己的回文后缀,所以指针指向,可以看着代码模拟一下,最后会是节点,那么我们再更新到当前节点,最后如下图:
2、插入字符
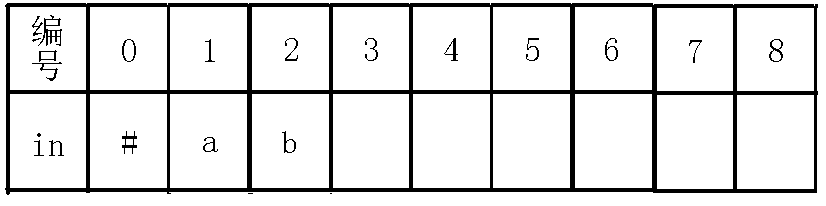
节点为号节点,那么,即,这个时候我们判断的其实是在的两边是不是都是,如果是的话那么肯定是回文串,可是这里并不匹配,所以跳指针到节点,但是我们发现,即,这个时候我们判断的实质是,我们把回文串的范围由刚才的个变为了个,现在考虑是不是有两个在一起构成回文串,可是还是失配了,所以我们再跳指针到节点,而这时其实就是自己匹配自己了,也就是,所以,也就是1,因为这个回文串就自身,长度自然为,我们像上面一样连边:

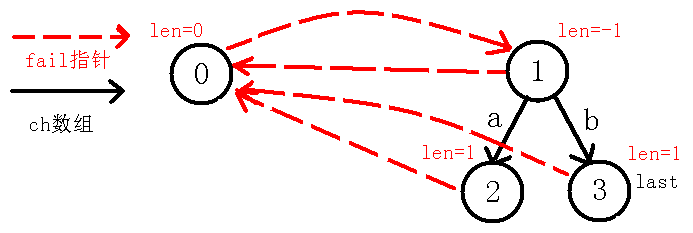
我们像上面一样求点的指针,因为我们需要找到的最长回文后缀,但是我们可以直接看出,除了自身之外就没有回文后缀了,所以它的指针指向节点,并且下移节点到,自己模拟代码也可以知道,如下图:
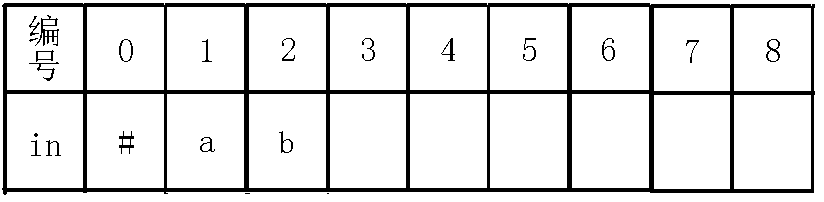
3、插入字符:
我们看到节点,而此时我们发现,即,也就是在考虑在节点(也就是回文串)的左右是不是都是字符,如果是的话,那么就找到了更长的回文串,但是现在失配了,所以我们跳指针到节点,此时了,也就是,也就是说我们找到了一个长度为的回文串,而节点没有向的转移,于是我们就连一条的转移到新的节点,此节点表示回文串,如下图:
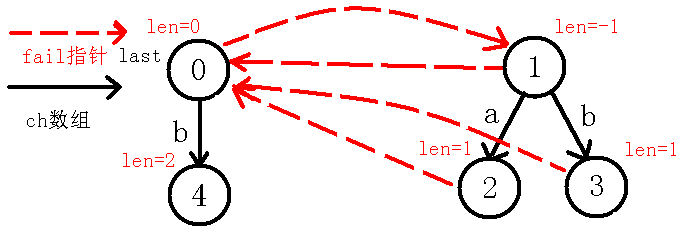
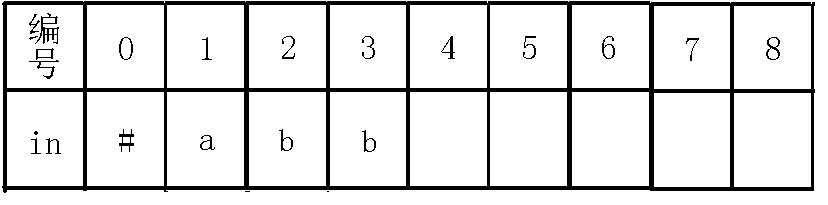
那么我们考虑求出号节点的指针,我们可以看出除了自身回文串()之外,是它的回文后缀的就是它的最后一个字母,那么我们就应该指向已有的代表这个回文串的节点,即号节点,至于怎么找的后文的例子可以更形象的说明!所以这里不再赘述,最后更新,操作完后如下:
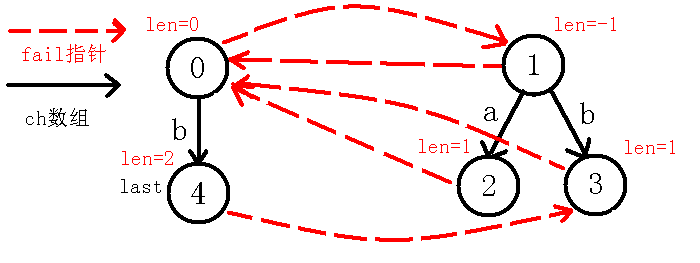
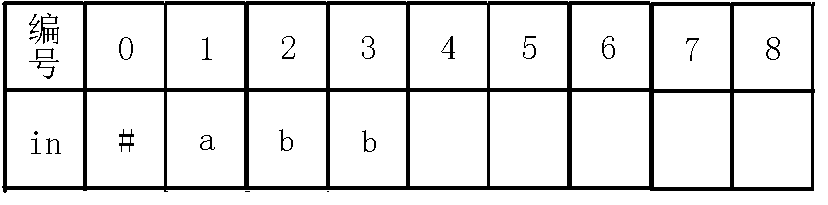
4、插入字符:
我们看着现在的节点,可以看出,即,也就是说,我们在节点的基础上,即回文串的两边都找到了字符,可以构成一个新的长度为的回文串,而节点没有的转移,于是就新建节点,并连边,如下图:
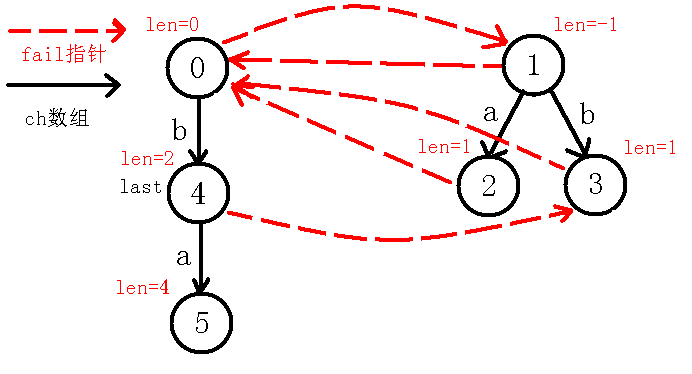
【重点】:
那么,我们现在考虑求出号节点的指针,指针是要求出当前回文串的不包括自己的最长回文后缀,因为现在节点在号节点,我们定义一个新的变量来跳指针,跳到号节点,不让改变,(可能会有人问为什么先跳再判断呢,为什么不先判断号节点即,而要先跳到节点去判断呢?那是因为判断号节点其实就是本身这个回文串,即,而我们说指针指向的是不包括自己的最长回文后缀),那么我们跳到节点之后发现即,也就是串不是回文串,我们再跳指针到节点,此时也就是,因为不是回文串,继续跳指针,我们到了节点,判断此时的(一定会等于的,因为现在是自己匹配自己,即),说明号节点的最长回文后缀为,所以指向代表回文串的节点,即号节点,并且更新节点,如下图:
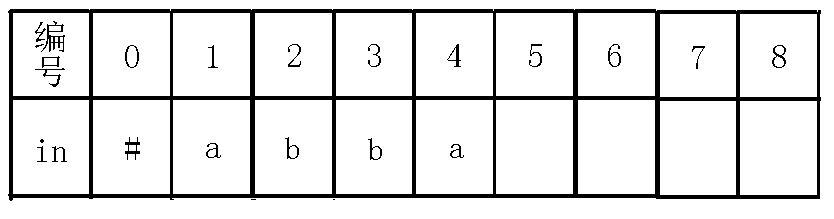
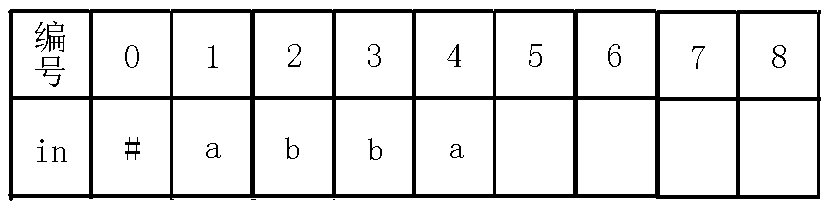
5、插入字符:
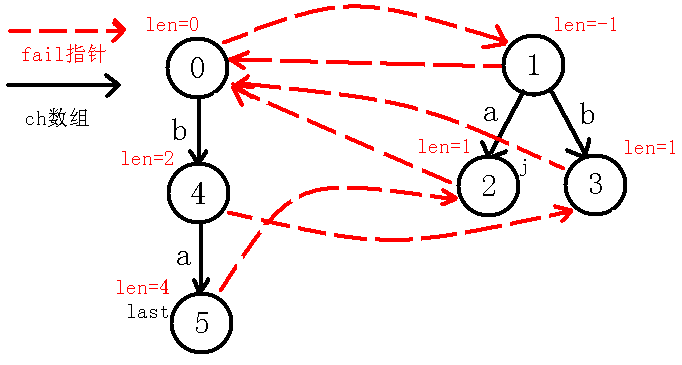
我们继续像上面一样模拟,看到节点,我们发现,也就是,我们这个操作实际上是找 两端是否相同,如果相同则说明能够成新的回文串,然而失配了。。于是我们继续跳指针,到了号节点,我们发现,即,也就是的两端相不相等,我们又发现不相等,于是又跳指针,到了节点,我们发现此时,也就是,说明我们找到了新的回文串,而节点并没有的转移(也就是以前没找到回文串 ),我们新加一条边到新的节点,如下图:
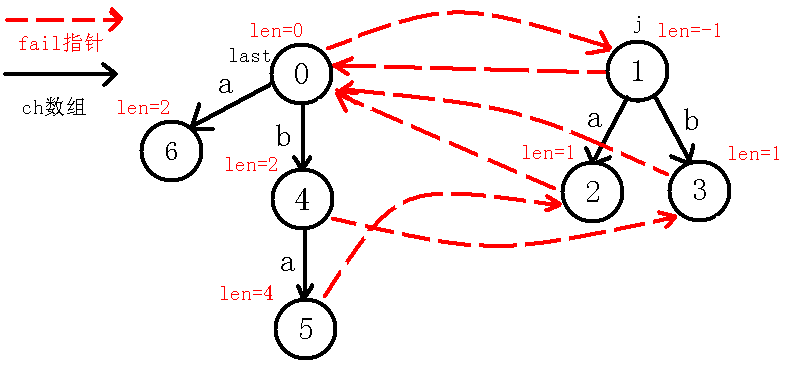
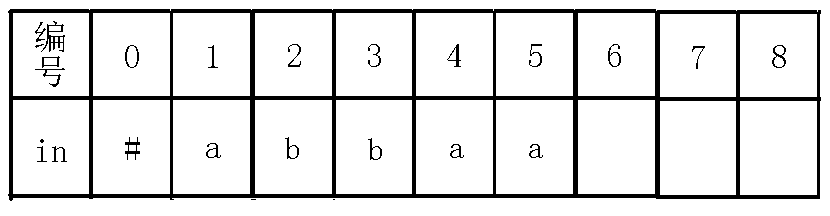
我们继续向上面一样求指针,跳指针到号节点,而此时也就是,即自己匹配了自己,所以回文串的除自身外最长回文后缀就是,所以为表示回文串的节点,即号节点,同时下移,操作完后如下图:
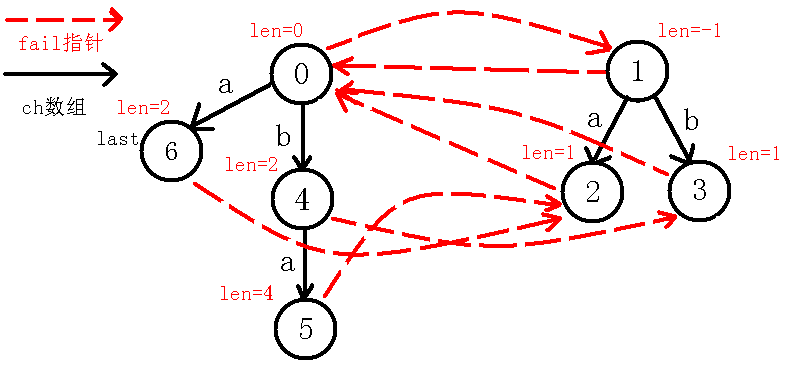
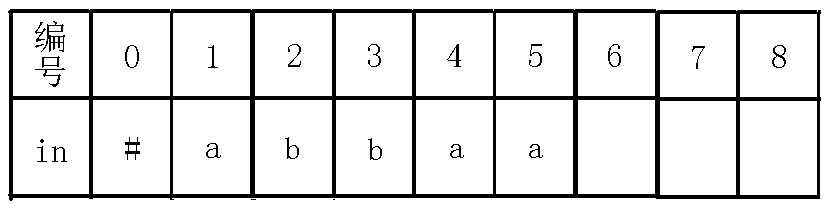
(后文的插入就留给你们自己动手模拟了,本人就贴个图了,我觉得应该要给你们自己动手实战一下,其实是本人太懒)
6、插入字符

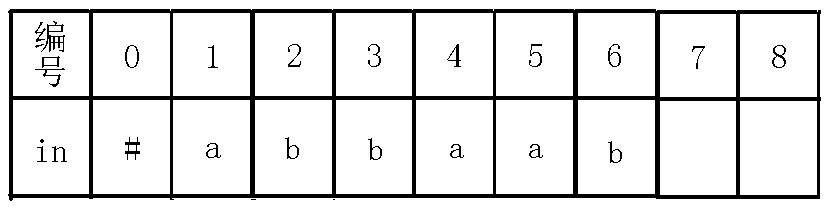
7、插入字符:
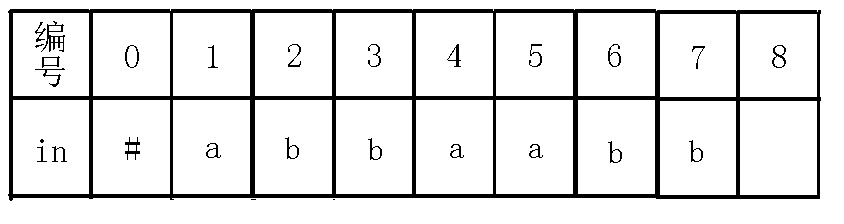
8、插入字符:

尾声:
本篇文章到此结束,如果觉得有帮助的话,希望能够点个赞



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】