深搜,广搜,最小生成树,最短路径简单总结(第六章图的总结)
1、首先这里讲了图的定义以及图的基本术语
图的基本术语有:(1)子图;(2)无向完全图和有向完全图;(3)稀疏图和稠密图;
(4)权和网 :带权的图通常称为网;
(5)邻接点;(6)度、入度和出度;
(7)路径和路径长度:
🔺路径长度是一条路径上经过的边或弧的数目;
(8)回路或环:第一个顶点和最后一个顶点相同的路径称为回路或者环;
(9)简单路径、简单回路或简单环:1)序列中顶点不重复出现的路径称为简单路径。
2)除了第一个顶点和最后一个顶点之外,其余顶点不重复出现的回路,称为简单回路或简单环;
(10)连通、连通图和连通分量;(如果连通分量是图本身,则此图是连通图);
(11)强连通图和强连通分量:(针对有向图)
强连通分量:极大强连通子图称作有向图的强连通分量;
🔺(12)连通图的生成树:一个极小连通子图,它含有图中全部顶点,但只有足以构成一棵树的n-1条边,这样的连通子图称为连通图的生成树。
(13)有向树和生成森林
2、图的存储结构
1、邻接矩阵(实际上就是一个二维数组)
利用邻接矩阵创建无向图
1 const int maxn = 1e5+5;//这里根据题目而定; 2 const int INF = 0x3f3f3f3f;//定义无穷大; 3 int vexnum , arcnum //定义点数和边数; 4 int G[maxn][maxn]; 5 int v1,v2,w;//输入的两个顶点和权值; 6 scanf("%d%d",&vexnum,&arcnum); 7 for(int i = 0 ; i < vexnum ;i++) 8 { 9 for(int j = 0 ; j < vexnum ;j++) 10 { 11 if(i==j) 12 { 13 G[i][j] = 0; 14 }else 15 G[i][j] = INF; 16 } 17 } 18 for(int i = 0 ; i < arcnum ;i++) 19 { 20 scanf("%d%d%d",&v1,&v2,&w); 21 G[v1][v2] = w; 22 G[v2][v1] = w;//因为是无向图,所以正反两边都得建一次; 23 }
2、邻接表(实际上就是一维数组+指针)
(1)表头结点表;
表头结点包括数据域和链域两部分;
(2)边表;
边表包括邻接点域、数据域和链域三部分;
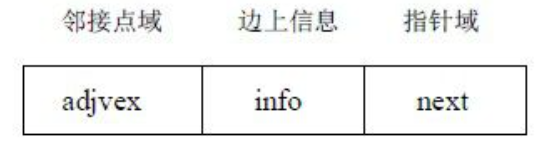
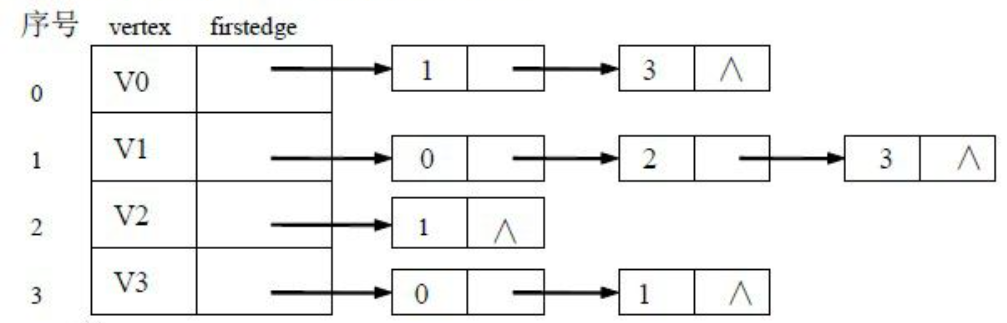
采用邻接表创建无向图
1 const int maxn = 1e5+5;//这里视题目而定; 2 struct ArcNode{ 3 int adjv;//邻接点,这里我假设为整型; 4 int w; //权值; 5 struct ArcNode *next1; //指向下一个结点的指针; 6 }p1,p2; 7 struct VNode{ 8 int data; //表头的数据;这里假设为整型; 9 ArcNode *firstarc; //第一个指向的结点; 10 }G[maxn]; 11 int vexnum , arcnum; 12 int v1,v2,w; 13 int main() 14 { 15 scanf("%d%d",&vexnum,&arcnum);//输入顶点数和边数; 16 for(int i = 0 ; i < vexnum;i++) 17 { 18 scanf("%d",&G[i].data); 19 G[i].firstarc = NULL; 20 } 21 for(int i = 0 ; i < arcnum ;i++) 22 { 23 scanf("%d%d%d",&v1,&v2,&w); 24 p1 = new ArcNode;//创建一个空间 25 p1->adjv = v2; //下面便是读入数据; 26 p1->next1 = G[i].firstarc; 27 p1->w = w; 28 G[i].firstarc = p1; 29 p2 = new ArcNode; 30 p2->adjv = v1; 31 p2->next1 =G[i].firstarc; 32 p2->w = w; 33 G[i].firstarc = p2; 34 } 35 }
3、图的遍历
1、深度优先搜索(dfs)
总结起来就三段话
1)递归;2)是否被访问过,用vis标记;3)连通分量(除非是一张连通图,不然一次dfs访问的是一个连通分量);
(1)采用邻接矩阵表示图的深度优先搜索遍历
1 const int maxn = 5e5+5;//根据具体题目分析; 2 int G[maxn][maxn];//图为邻接矩阵类型,从第v个顶点出发深度优先搜索遍历图; 3 bool vis[maxn]; 4 int vexnum;//点数; 5 void dfs(int v) 6 { 7 printf("%d",v); 8 vis[v] = 1; //标记为被访问过; 9 for(int i = 0 ; i < vexnum ;i++) 10 { 11 if(G[v][i]!=0&&!vis[i]) //如果有边且未被访问过; 12 { 13 vis[i] = 1; //标记为被访问过; 14 dfs(i); //深搜; 15 } 16 } 17 }
2、利用邻接表表示图的深搜;
1 const int maxn = 1e5+5;//这里视题目而定; 2 struct ArcNode{ 3 int adjv;//邻接点,这里我假设为整型; 4 int w; //权值; 5 struct ArcNode *next1; //指向下一个结点的指针; 6 }p1,p2; 7 struct VNode{ 8 int data; //表头的数据;这里假设为整型; 9 ArcNode *firstarc; //第一个指向的结点; 10 }G[maxn]; 11 int vexnum , arcnum; 12 int v1,v2,w; 13 bool vis[maxn]; 14 ArcNode p; 15 void dfs(int v) 16 { 17 printf("%d",v); 18 vis[v] = 1; 19 p = G[v].firstarc; 20 int w ; 21 while(p!=NULL) 22 { 23 w = p->adjv; 24 if(!vis[w]) 25 dfs(w); 26 p = p->next1; 27 } 28 } 29 int main() 30 { 31 scanf("%d%d",&vexnum,&arcnum);//输入顶点数和边数; 32 for(int i = 0 ; i < vexnum;i++) 33 { 34 scanf("%d",&G[i].data); 35 G[i].firstarc = NULL; 36 } 37 for(int i = 0 ; i < arcnum ;i++) 38 { 39 scanf("%d%d%d",&v1,&v2,&w); 40 p1 = new ArcNode; 41 p1->adjv = v2; 42 p1->next1 = G[i].firstarc; 43 p1->w = w; 44 G[i].firstarc = p1; 45 p2 = new ArcNode; 46 p2->adjv = v1; 47 p2->next1 =G[i].firstarc; 48 p2->w = w; 49 G[i].firstarc = p2; 50 } 51 }
2、广度优先搜索(bfs)
1 void bfs(int v) //bfs函数; 2 { 3 vis[v] = 1; //一进来就标记为访问过; 4 queue<int>q; //实际上bfs就是层序遍历,需要用到队列; 5 int tmp; //一个暂时的变量; 6 q.push(v); //入队; 7 while(!q.empty())//当队列为非空时; 8 { 9 tmp = q.front(); //取出队头元素; 10 printf(" %d",tmp); //输出; 11 q.pop();//记得出队,不然会变成死循环; 12 for(int i = 0 ; i < N ;i++) 13 { 14 if(G[tmp][i]==1&&vis[i]==0)//如果有边,而且没被访问过; 15 { 16 vis[i] = 1; //标记已被访问; 17 q.push(i); //如果满足条件则入队; 18 } 19 } 20 } 21 22 }
4、图的应用
1、最小生成树
在一个连通网的所有生成树中,各边的代价之和最小的那棵生成树称为该连通网的最小代价生成树,简称最小生成树;
有两个算法 1、普里姆算法 和克鲁斯卡尔算法
1)普里姆算法
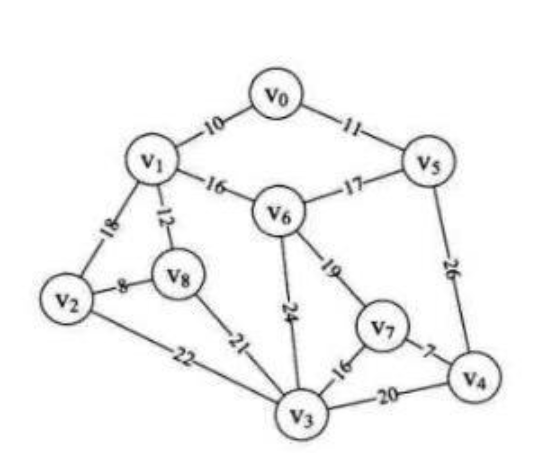

普里姆算法的步骤
从图中某一个顶点出发(这里选V0),寻找它相连的所有结点,比较这些结点的权值大小,然后连接权值最小的那个结点。(这里是V1)然后将寻找这两个结点相连的所有结点,找到权值最小的连接。(这里是V5).重复上一步,知道所有结点都连接上。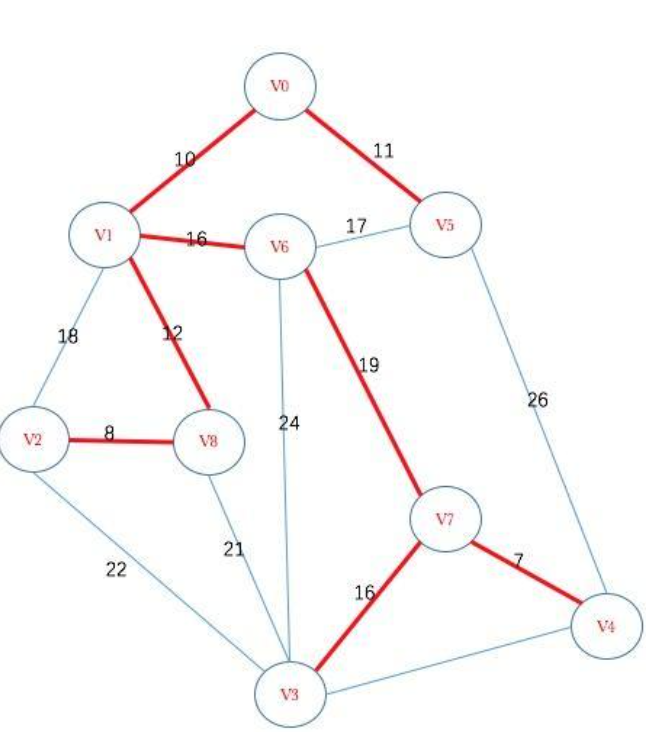
2)克鲁斯卡尔
边思想,不断找不同集合的最小边连接,直到所有点都在同个集合;
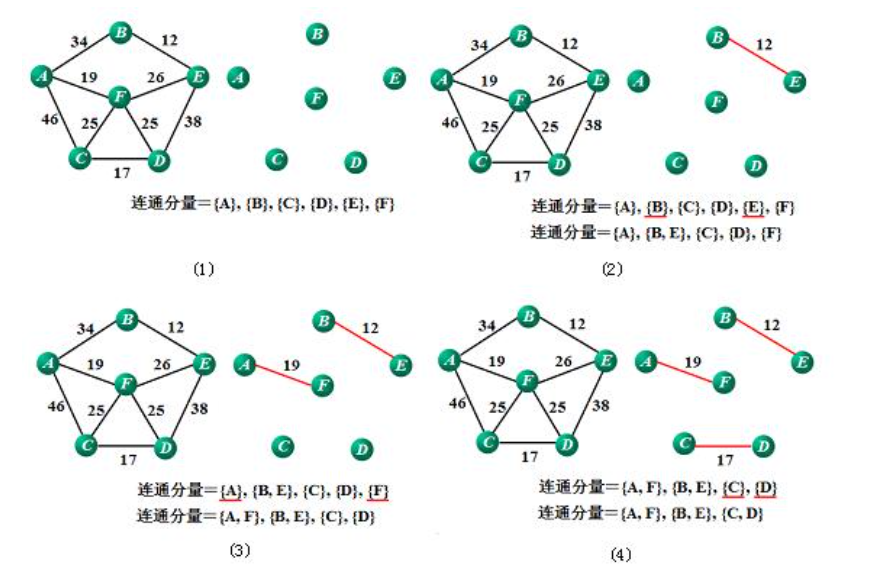
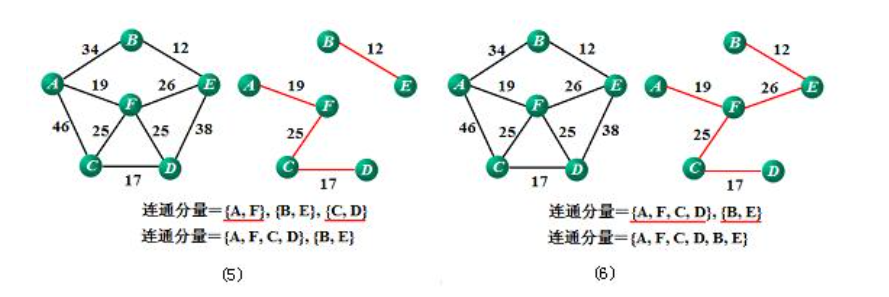
最小生成树的代码在这里先不说了,我自己竟然写的是并查集,以后有机会再说吧;
接下来还学习了最短路径
单源最短路径迪杰斯特拉算法:
(1)首先先解释一下单源最短路径:
1)容易的解释:指定一个点(源点)到其余各个顶点的最短路径,也叫做“单源最短路径”
2)官方解释:给定一个带权有向图G=(V,E),其中每条边的权是一个实数。另外,还给定V中的一个顶点,称为源。现在要计算从源到其他所有各顶点的最短路径长度。这里的长度就是指路上各边权之和。这个问题通常称为单源最短路径问题。
(2)解释一下Dijkstra算法:
例如求A点到B、C、D、E、F顶点的最短路径;
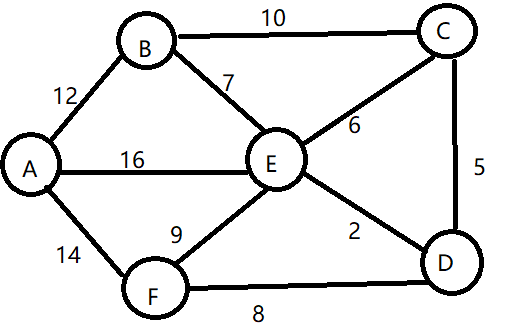
我们可以先这样设想:
1)先把所有的点到另一个点的长度全部初始化为无穷大 ,本身到本身则初始化为0,再输入数值;
第一:将所有点到点初始化为无穷大

代码大致如下:
1 const int INF = 0x3f3f3f3f; //为无穷大;
2 int G[2000][2000];
3 int N ;//N为点的个数;
4
5 for( i = 1 ;i <= N ;i++)
6 {
7 for( j = 1 ;j <= N ;j++)
8 {
9 G[i][j] = INF;
10 }
11 }
也可用下面这种:
1 #include<string.h> 2 const int INF = 0x3f3f3f3f; 3 int N; //点的个数; 4 int G[2000][2000]; 5 memset(G,INF,sizeof(G));
第二:将本身到本身初始化为0 ;因为本身到本身的距离就为0;
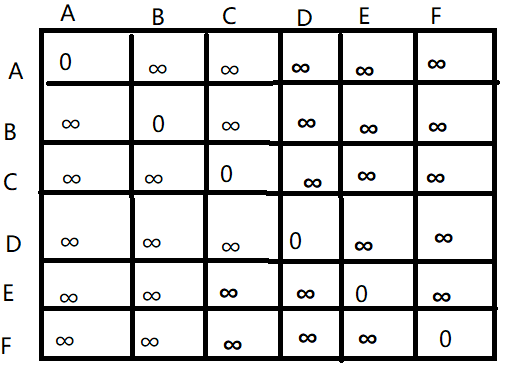
1 for(int i = 1 ;i <= N; i++)
2 {
3 G[i][i] = 0; //本身到本身距离为0;
4 }
第三:输入数据:

对应下面的表格:
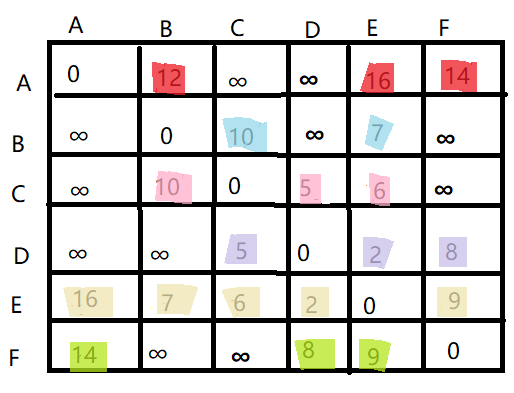
代码实现大概如下:
1 int M; //M为边的个数;
2 int x , y; // x ,y 为同一边的两个点;
3 int D; //D 为题目给的边的权值;
4 for( i = 1; i <= M ;i++)
5 {
6 cin>>x>>y>>D;
7
8 if(G[x][y]>D)
9 {
10 G[x][y] = D;
11 G[y][x] = D;
12 }
13
14 }
15
16
17 //上面我们已经把点到其他点的距离初始化为无穷大,把本身到本身初始化为0;
//那么上面这个循环的化,我们可以把题目给的两点之间的权值输入;
18 //题目给的权值一定为正值,所以比0大,故本身到本身的距离还是维持为0;
//而小于无穷大,所以用上面那个循环可把边的权值输入;
2)我们还需用一个一维数组d来存储A顶点到其余各个顶点的初始路程

下面我们来模拟一下:
这是输入最初数据的表格:

模拟:
1)既然是从A点到其余各个顶点的最短路径,那就先找一个离A号顶点最近的顶点。 A到B的距离最小
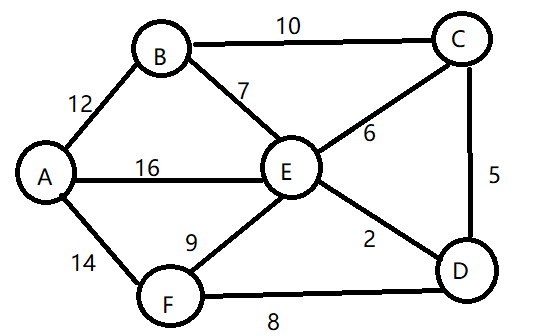
所以d[2]的值就已经从“估计值”变成了“确定值”,目前离A顶点最近的是B顶点。
2)既然选了B点,接下来看B顶点有哪些出边呢,有B->E和B->C两条边。
先讨论B->E能否让A顶点到E顶点的路程变短;
A->B->E :d[2]+e[2][5]表示从A到B到E的距离;d[2]是A到B顶点的路程,e[2][5]表示B到E的距离; 12+7 = 19;
A->E :d[5] = 16;
我们发现 d[2]+e[2][5]=19,d[5] = 16; 所以 d[5] < d[2]+e[2][5];
所以A到E目前的最短距离为16;
d
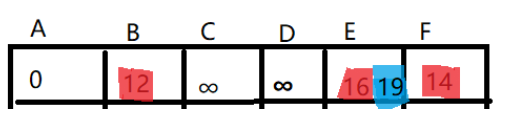
因此d[5]更新为 16;(这个过程有个专业术语叫做:松弛);
d 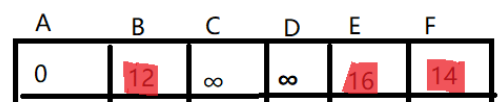
再判断B->C
A->B->C:d[2]+e[2][3] 表示A到B到C的距离;d[2]是A到B顶点的路程,e[2][3]表示B到C 的距离;12+10 = 22;
A->C:A没有直接到C ,所以为无穷大;
22<无穷大
所以A到C目前的最短距离为22;d[3] = 22;

这样从A到B的当前最短路径就更新完了;
3)找除B外离A最近的点:由图可知是F点;

由图可知F的出边有两条:F->E, F->D;
先讨论 F->E能否让A到E的距离变短;
A->F->E :d[6]+e[6][5] = 14+ 9 = 23;
A->E :d[5] = 16;
所以d[5] < d[6]+e[6][5];
所以当前A到E的最短距离为16; d[5] = 16;

再讨论E->D的距离能否让A到D的距离变短
A->E->D : d[5]+e[5][4] = 16+2=18;
A->D : 无穷大;
所以A到D的当前最短距离更新为18; d[4] = 18;

4)找除B和F外离A最近的点:即E点
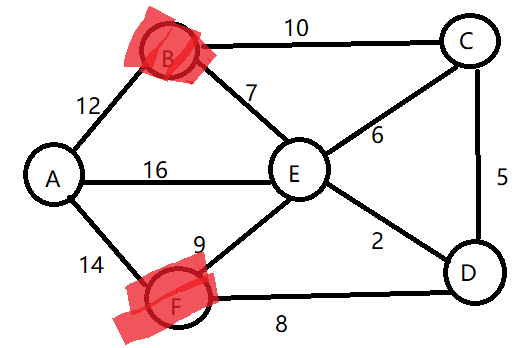
E的出边有C和D,看E->C和E->D能否使A到C的距离变短,使A到D的距离变短;
先讨论E->D
A->E->D :d[5]+e[5][4] = 16+2 = 18
之前更新后的AD d[4] = 22;
所以AD 当前最短变为18; d[4] = 18;

讨论E->C,看是否让AC变短
A->E->C :d[5]+e[5][3] = 16+6 =22;
原更新的AC为22;
所以当前AC最短为22; d[3] = 22;
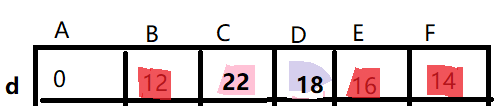
5)找除B,E,F外离A最近的点,即D

D的出边只有D->C;
看D->C,能否让AC变短;
A->D->C d[4]+e[4][3] = 18+5 = 23;
原AC 22;
所以AC当前最短为22; d[3] = 22;

6)最后剩下C
全部找完,确定了A到各个点的最短路径;
还有做了老师布置的一道作业和实践题
作业题:
给定一个有N个顶点和E条边的无向图,请用DFS和BFS分别列出其所有的连通集。假设顶点从0到N−1编号。进行搜索时,假设我们总是从编号最小的顶点出发,按编号递增的顺序访问邻接点。
输入格式:
输入第1行给出2个整数N(0<N≤10)和E,分别是图的顶点数和边数。随后E行,每行给出一条边的两个端点。每行中的数字之间用1空格分隔。
输出格式:
按照"{ v1 v2 ... vk }"的格式,每行输出一个连通集。先输出DFS的结果,再输出BFS的结果。
输入样例:
8 6
0 7
0 1
2 0
4 1
2 4
3 5
输出样例:
{ 0 1 4 2 7 }
{ 3 5 }
{ 6 }
{ 0 1 2 7 4 }
{ 3 5 }
{ 6 }
代码如下:
1 #include<iostream> 2 #include<stdio.h> 3 #include<string.h> 4 #include<queue> 5 using namespace std; 6 7 int N ,M ; //输入点数和边数; 8 int G[15][15];//将图存在邻接矩阵中,因为题目N较小,综合下来用邻接矩阵方便; 9 bool vis[15];//用来记录是否已被访问过; 10 int x , y; 11 void dfs(int v) //dfs函数; 12 { 13 vis[v] = 1; //一进来就标记为被访问过; 14 for(int i = 0 ; i < N ;i++) //遍历; 15 { 16 if(G[v][i]==1&&vis[i]==0) //如果有边而且还未没被访问过; 17 { 18 vis[i] = 1; //标记被访问过; 19 printf(" %d",i); //并输出; 20 dfs(i);//利用递归继续深搜; 21 } 22 } 23 } 24 void bfs(int v) //bfs函数; 25 { 26 vis[v] = 1; //一进来就标记为访问过; 27 queue<int>q; //实际上bfs就是层序遍历,需要用到队列; 28 int tmp; //一个暂时的变量; 29 q.push(v); //入队; 30 while(!q.empty())//当队列为非空时; 31 { 32 tmp = q.front(); //取出队头元素; 33 printf(" %d",tmp); //输出; 34 q.pop();//记得出队,不然会变成死循环; 35 for(int i = 0 ; i < N ;i++) 36 { 37 if(G[tmp][i]==1&&vis[i]==0)//如果有边,而且没被访问过; 38 { 39 vis[i] = 1; //标记已被访问; 40 q.push(i); //如果满足条件则入队; 41 } 42 } 43 } 44 45 } 46 int main() 47 { 48 scanf("%d%d",&N,&M);//输入点数和边数; 49 for(int i = 1 ; i <= M ;i++) 50 { 51 scanf("%d%d",&x,&y); 52 G[x][y] = 1;//输入邻接矩阵,注意这是一张无向图,所以正反都得输入; 53 G[y][x] = 1; 54 } 55 for(int i = 0 ;i < N ;i++) //将所有点遍历一遍,让所有连通分量都有被遍历过; 56 { 57 if(vis[i]==0)//如果没有被访问过; 58 { 59 printf("{");//格式; 60 printf(" %d",i); 61 dfs(i);//深搜; 62 printf(" }\n"); 63 } 64 } 65 memset(vis,0,sizeof(vis));//注意此时应将所有点标记成未访问过,进行广搜,memset的头文件为<string.h>; 66 for(int i = 0 ;i < N ;i++) 67 { 68 if(vis[i]==0)//如果没被访问过; 69 { 70 printf("{"); 71 bfs(i);//广搜; 72 printf(" }\n"); 73 } 74 } 75 return 0; 76 }
实践题:
在老电影“007之生死关头”(Live and Let Die)中有一个情节,007被毒贩抓到一个鳄鱼池中心的小岛上,他用了一种极为大胆的方法逃脱 —— 直接踩着池子里一系列鳄鱼的大脑袋跳上岸去!(据说当年替身演员被最后一条鳄鱼咬住了脚,幸好穿的是特别加厚的靴子才逃过一劫。)
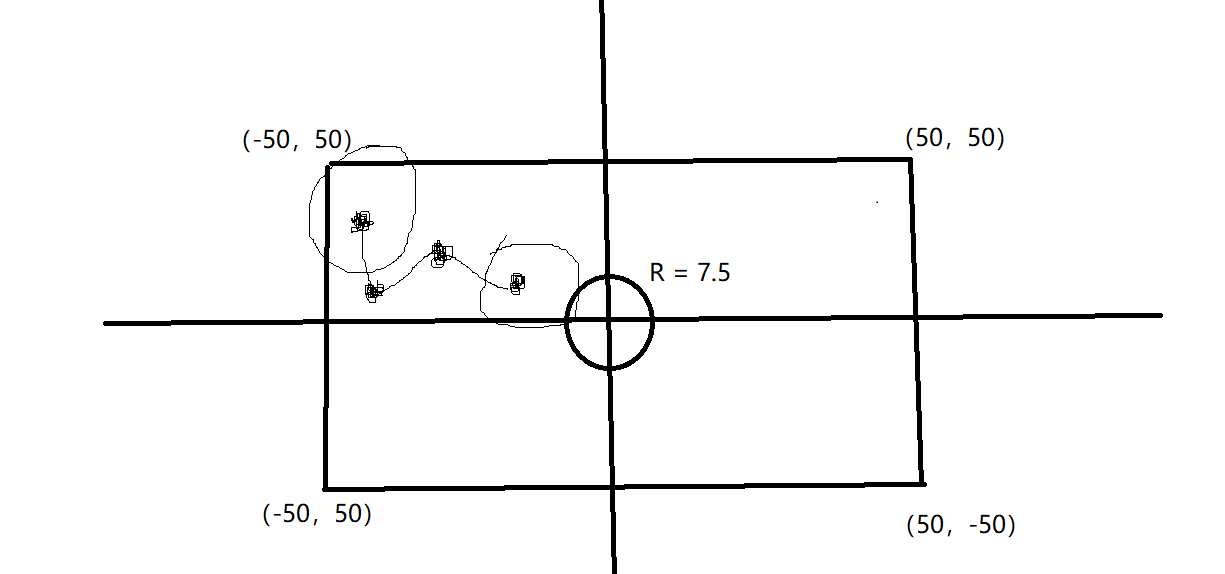
设鳄鱼池是长宽为100米的方形,中心坐标为 (0, 0),且东北角坐标为 (50, 50)。池心岛是以 (0, 0) 为圆心、直径15米的圆。给定池中分布的鳄鱼的坐标、以及007一次能跳跃的最大距离,你需要告诉他是否有可能逃出生天。
输入格式:
首先第一行给出两个正整数:鳄鱼数量 N(≤100)和007一次能跳跃的最大距离 D。随后 N 行,每行给出一条鳄鱼的 (x,y) 坐标。注意:不会有两条鳄鱼待在同一个点上。
输出格式:
如果007有可能逃脱,就在一行中输出"Yes",否则输出"No"。
输入样例 1:
14 20
25 -15
-25 28
8 49
29 15
-35 -2
5 28
27 -29
-8 -28
-20 -35
-25 -20
-13 29
-30 15
-35 40
12 12
输出样例 1:
Yes
输入样例 2:
4 13
-12 12
12 12
-12 -12
12 -12
输出样例 2:
No
解题思路:这是在我画图之后想到的,先深搜找连通分量,然后将连通分量染色,然后看是否有连通分量满足题意
第一个flag1是判断是否连接矩形,我判断的是直线距离,
其实本应该判断的是以连通块某点为圆心以那个最大距离为半径与矩形是否有交点,
但是其实判断直线距离就好了,flag2是判断连通块的点是否与小岛圆有交点
大概思路如上,由这张图思考而来的;
![]()
代码如下:
1 #include<iostream> 2 #include<stdio.h> 3 #include<cmath> 4 using namespace std; 5 6 int N ; //鳄鱼的个数; 7 int maxdis; //跳的最大距离; 8 struct zb{ 9 int u; //点的横坐标; 10 int v; //点的纵坐标; 11 }G[105];//图中点的信息 12 double map[105][105];//图中点与点的距离; 13 double getdis(int i ,int j) //获得两点间的距离; 14 { 15 double d = sqrt((G[i].u-G[j].u)*(G[i].u-G[j].u)+(G[i].v-G[j].v)*(G[i].v-G[j].v)); 16 return d; 17 } 18 int tp1 , tp2; //输入的横坐标和纵坐标; 19 bool vis[105]; //标记点是否被访问过; 20 int color[105]; //用于将连通块染色; 21 int count1 = 1; //用于染色的记数, 22 23 void dfs(int x) //深搜,找连通块; 24 { 25 vis[x] = 1; //标记该点访问过; 26 for(int i = 1 ; i<= N ;i++) 27 { 28 if(x!=i&&vis[i]==0&&map[x][i]<=maxdis)//如果另一点还没被访问过,且两点间距离小于最大距离; 29 { 30 color[i] = count1; //将连通的染为同种颜色; 31 vis[i] = 1; //标记访问过; 32 dfs(i); //继续深搜; 33 } 34 } 35 } 36 37 int main() 38 { 39 scanf("%d%d",&N,&maxdis); //输入鳄鱼的个数和最大距离; 40 for(int i = 1 ; i <= N ;i++) 41 { 42 scanf("%d%d",&tp1,&tp2); 43 G[i].u = tp1; //将输入的横坐标赋给图的点的横坐标; 44 G[i].v = tp2; //将输入的纵坐标赋给图的点的纵坐标; 45 } 46 for(int i = 1 ; i <= N ;i++) 47 { 48 for(int j = 1 ; j <= N ;j++) 49 { 50 if(i!=j) 51 { 52 map[i][j] = map[j][i] = getdis(i,j);//将距离存成图中的边; 53 } 54 } 55 } 56 for(int i = 1 ; i <= N ;i++) 57 { 58 if(vis[i]==0) 59 { 60 color[i] = count1 ; //染色; 61 dfs(i); 62 count1++; //代表不同的连通块,染不同的颜色; 63 } 64 } 65 66 67 int flag1 = 0 ,flag2 = 0; //flag1标记是否与矩形相连,flag2标记是否与小岛圆相连; 68 for(int i = 1 ; i <= count1 ;i++) //遍历各个连通块; 69 { 70 flag1 = 0 , flag2 = 0;//用于判断同个连通块是否同时满足两个条件; 71 for(int j = 1 ; j <= N ;j++) 72 { 73 if(color[j]==i) //如果是同一个连通块 74 { 75 if(G[j].v+maxdis>=50||G[j].v-maxdis<=-50||G[j].u+maxdis>=50||G[j].u-maxdis<=-50) 76 { 77 flag1 = 1; 78 }//与矩形相连; 79 80 if((G[j].u)*(G[j].u)+(G[j].v)*(G[j].v)<=(7.5+maxdis)*(7.5+maxdis)) 81 { 82 flag2 = 1; 83 }//与小岛圆相连; 84 } 85 } 86 87 if(flag1==1&&flag2==1)//如果同一个连通块同时满足两个条件; 88 { 89 printf("Yes\n"); 90 return 0; 91 } 92 93 } 94 printf("No\n"); 95 return 0; 96 }
总结:这一章感觉学了挺多东西,希望接下来再接再厉,继续努力;
下一章的目标:好好学习,灵活应用!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号