(原）数据结构之树状数组详解

树状数组

树状数组是一个查询和修改复杂度都为log(n)的数据结构。

主要用于数组的单点修改&&区间求和.

另外一个拥有类似功能的是线段树

🔺树状数组（Binary Indexed Tree) ------解决动态前缀和问题的数据结构

 

1、对于询问操作（复杂度为logN）

 查询前缀和

（1）首先了解管辖区域：设节点编号为x，那么这个节点管辖的区间为2^k，（其中k为二进制末尾0的个数）个元素；

什么意思呢；

 

 

例：1）设我们一共有n个元素：a1，a2，a3，.........an，设管辖数组为d[ ] ；

则    d[6] = a5 + a6；    这是为什么呢；

看6的二进制形式为110   末尾有一个零 ，则管辖的区间为2^1 = 2个元素

 

2）再看d[8] = a1+a2+....+a8;  共8个元素  

因为8的二进制为1000  ，末尾有三个零，则管辖的区间为2^3 = 8 个元素；

 

以下面这幅图为例

 

 

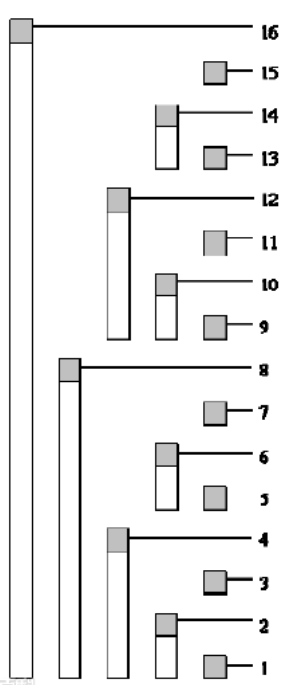
（2）了解如何查询前缀和：

例：假设我们要查13这个位置的前缀和：

那么怎么知道为多少呢。

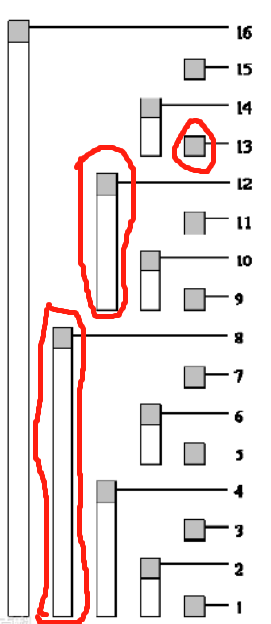
实际上就查询这三部分，那么这三部分是怎么来的

将13 化为2进制

1101 = 13；   管辖2^0 = 1个元素

现将末尾的1去掉变成

1100 = 12；管辖2^2 = 4个元素；

再将末尾的1去掉变成

1000 = 8；管辖2^3 = 8个元素

 

加起来刚好也是13个元素；

实际上13的前缀和为d[13]+d[12]+d[8] （这里也可以验证一个区间内的元素不会超过logn个，所以单次查询的复杂度最多为logn）

所以实际上如果要求这个我们就需要知道最低位的1在哪，将其减掉。

（3）了解lowbit函数（这是一个求最低位1的函数）

代码写起来非常简单，如下：

int lowbit(int x)

{
    
    return x&(-x);
    
} 

为什么是这样写呢：x与其负数；

首先从二进制的负数说起

在二进制中负数是以补码形式存在的

例   假设我们求12的最低1的位

12 的二进制为   1100；

其负数为  取反＋1    ：0011+1 = 0100  

将两个相与变成   1100&0100 = 0100 便找到最低位的1 了；这样我们就可以实现刚刚上面的过程了。

 

🔺所以上面的查询功能的代码可以这样写

代码如下：

int lowbit(int x)
{
    
    return x&(-x);    
} 

int Query(int x)
{
    int ans = 0 ;
    while(x)
    {
        ans += d[x];
       x -= lowbit(x);
    }15 }

2、对于修改操作（复杂度为logN）（复杂度分析和上面一样）

 （单点修改）

其实是上面操作的逆操作

 

 

还是以上面那幅图来说

 

 

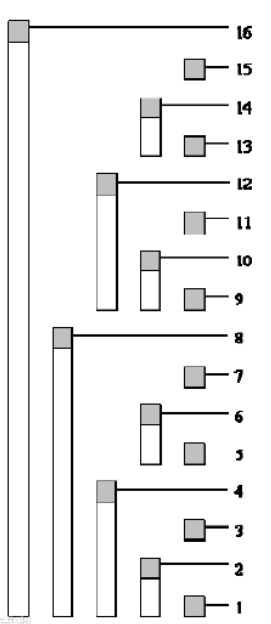
 假设我们要修改6，那么对于应该修改图中的标红部分，应该都有贡献

也就是图中的6，8，16；那么这是怎么算出的呢，这其实是上面的逆操作；

 

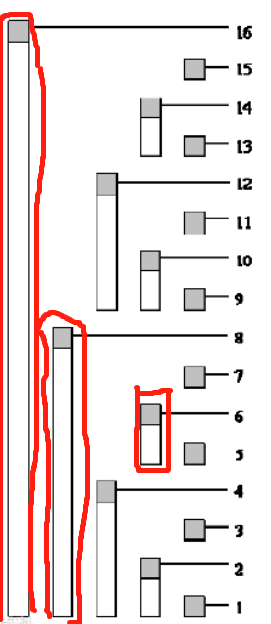
以二进制来看，

6 = 110；    末尾的0为1个 所以，2^1 = 2;

 6+2  = 110 + 010 = 1000 = 8；

8 的末尾0有2个， 所以 2^3 = 8 ;

所以下一个数为 

1000+1000 = 8+8 = 16；

其实就是上面的逆过程；

所以修改6的话，应该修改的数有 6， 8，16；

 

代码如下：

int lowbit(int x)
{
    
    return x&(-x);    
} 

void Update(int x ,int value)//对a[x]加上value;
{
    while(x<=n)
    {
        d[x] += value;
        x += lowbit(x);
    }
}