(原创)BZOJ 2038 小Z的袜子(hose) 莫队入门题+分块
I - 小Z的袜子(hose)
作为一个生活散漫的人,小Z每天早上都要耗费很久从一堆五颜六色的袜子中找出一双来穿。终于有一天,小Z再也无法忍受这恼人的找袜子过程,于是他决定听天由命……
具体来说,小Z把这N只袜子从1到N编号,然后从编号L到R(L 尽管小Z并不在意两只袜子是不是完整的一双,甚至不在意两只袜子是否一左一右,他却很在意袜子的颜色,毕竟穿两只不同色的袜子会很尴尬。
你的任务便是告诉小Z,他有多大的概率抽到两只颜色相同的袜子。当然,小Z希望这个概率尽量高,所以他可能会询问多个(L,R)以方便自己选择。
输入文件第一行包含两个正整数N和M。N为袜子的数量,M为小Z所提的询问的数量。接下来一行包含N个正整数Ci,其中Ci表示第i只袜子的颜色,相同的颜色用相同的数字表示。再接下来M行,每行两个正整数L,R表示一个询问。
Output包含M行,对于每个询问在一行中输出分数A/B表示从该询问的区间[L,R]中随机抽出两只袜子颜色相同的概率。若该概率为0则输出0/1,否则输出的A/B必须为最简分数。(详见样例)
Sample Input1 2 3 3 3 2
2 6
1 3
3 5
1 6
Sample Output
2/5
0/1
1/1
4/15
【样例解释】
询问1:共C(5,2)=10种可能,其中抽出两个2有1种可能,抽出两个3有3种可能,概率为(1+3)/10=4/10=2/5。
询问2:共C(3,2)=3种可能,无法抽到颜色相同的袜子,概率为0/3=0/1。
询问3:共C(3,2)=3种可能,均为抽出两个3,概率为3/3=1/1。
注:上述C(a, b)表示组合数,组合数C(a, b)等价于在a个不同的物品中选取b个的选取方案数。
【数据规模和约定】
30%的数据中 N,M ≤ 5000;
60%的数据中 N,M ≤ 25000;
100%的数据中 N,M ≤ 50000,1 ≤ L < R ≤ N,Ci ≤ N。
解题思路:这道题目是说给你n个数,m次查询,求l到r之间出现两个颜色相同的袜子的概率;即出现两个相同数字的概率;
莫队使用条件:必须是离线的查询,一般不能有修改操作(其实也有带修改的莫队);
这道题属于区间问题,但是用线段树解决不了这道题,这道题没有修改操作,我们可以用莫队分块来解决这道题;
我们可以试着推一下这道题:
以题目给的第一样例为例:
题目给6个数是 1 2 3 3 3 2
查询第2个数到第6个数之间相同的两个颜色的概率;
所以我们的分母一定是 (6-2)+1个数中取两个;即C(5,2);即长度去两个数 ,假设len = (l-r+1) ,即C(len,2);
分子则是出现的相同数字取2,以上面的样例为例,2到6区间中有2 3 3 3 2 ,则2出现了两次,3出现了三次,所以分子为C(2,2)+C(3,2);
所以概率为:(C(2,2)+C(3,2))/C(5,2);
依此类推:可以得到如下规律:
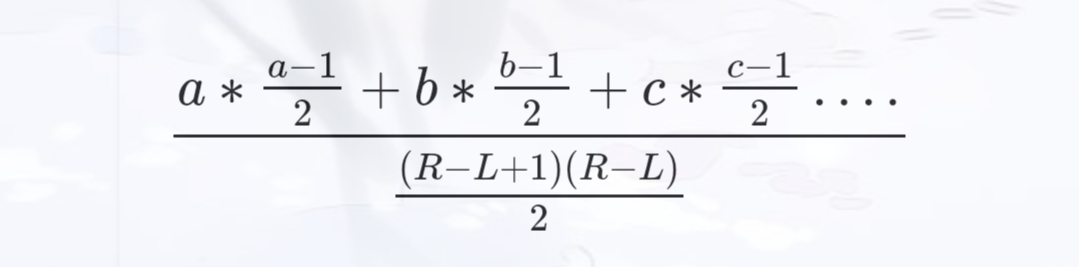
即(a^2+b^2+c^2+…x^2-(a+b+c+d+…..))/((R-L+1)*(R-L))
即(a^2+b^2+c^2+…x^2-(R-L+1))/((R-L+1)*(R-L))
代码如下:
1 #include<iostream> 2 #include<stdio.h> 3 #include<cmath> 4 #include<algorithm> 5 using namespace std; 6 7 8 9 typedef long long int ll; 10 const int maxn = 5e4+5; 11 int n , m; 12 ll blocksize; 13 ll ans = 0; 14 ll s[maxn]; 15 ll block[maxn]; 16 ll c[maxn]; 17 struct query{ 18 ll l ; 19 ll r ; 20 ll id; 21 ll fenzi; 22 ll fenmu; 23 }q[maxn]; 24 ll square(ll x) 25 { 26 27 return x*x; 28 29 } 30 ll gcd(ll a ,ll b) 31 { 32 if(b==0) 33 return a; 34 else 35 return gcd(b,a%b); 36 } 37 bool cmp(query a, query b) 38 { 39 if(block[a.l]==block[b.l]) 40 { 41 if(block[a.l]%2==1) 42 { 43 return a.r < b.r; 44 }else 45 return a.r > b.r; 46 }else 47 return block[a.l]<block[b.l]; 48 } 49 bool cmp2(query a , query b) 50 { 51 return a.id < b.id; 52 } 53 void add(int num) 54 { 55 ans -= square(s[c[num]]); 56 s[c[num]]++; 57 ans += square(s[c[num]]); 58 } 59 60 void remove(int num) 61 { 62 ans -= square(s[c[num]]); 63 s[c[num]]--; 64 ans += square(s[c[num]]); 65 } 66 void solve() 67 { 68 int l = 1 ; 69 int r = 0; 70 for(int i = 1 ; i <= m ;i++) 71 { 72 while(q[i].l<l) 73 { 74 l--; 75 add(l); 76 } 77 78 while(q[i].l>l) 79 { 80 remove(l); 81 l++; 82 } 83 while(q[i].r<r) 84 { 85 remove(r); 86 r--; 87 } 88 while(q[i].r>r) 89 { 90 r++; 91 add(r); 92 } 93 if(q[i].l==q[i].r) 94 { 95 q[i].fenzi = 0; 96 q[i].fenmu = 1; 97 continue; 98 } 99 ll x = ans - (q[i].r-q[i].l+1); 100 ll y = (q[i].r-q[i].l+1)*(q[i].r-q[i].l); 101 ll k = gcd(x,y); 102 q[i].fenzi = x / k; 103 q[i].fenmu= y / k; 104 } 105 } 106 107 int main() 108 { 109 scanf("%d%d",&n,&m); 110 blocksize = sqrt(n); 111 for(int i = 1 ; i <= n ;i++) 112 { 113 scanf("%d",&c[i]); 114 } 115 for(int i = 1 ; i <= n; i++) 116 { 117 block[i] = (i-1)/blocksize+1; 118 } 119 for(int i = 1 ;i <= m ;i++) 120 { 121 scanf("%d%d",&q[i].l,&q[i].r); 122 q[i].id = i; 123 } 124 125 sort(q+1,q+m+1,cmp); 126 solve(); 127 sort(q+1,q+m+1,cmp2); 128 for(int i = 1 ; i <= m ;i++) 129 { 130 printf("%lld/%lld\n",q[i].fenzi,q[i].fenmu); 131 132 } 133 return 0; 134 }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号