记忆化搜索的状态初始化问题

 初始化1：

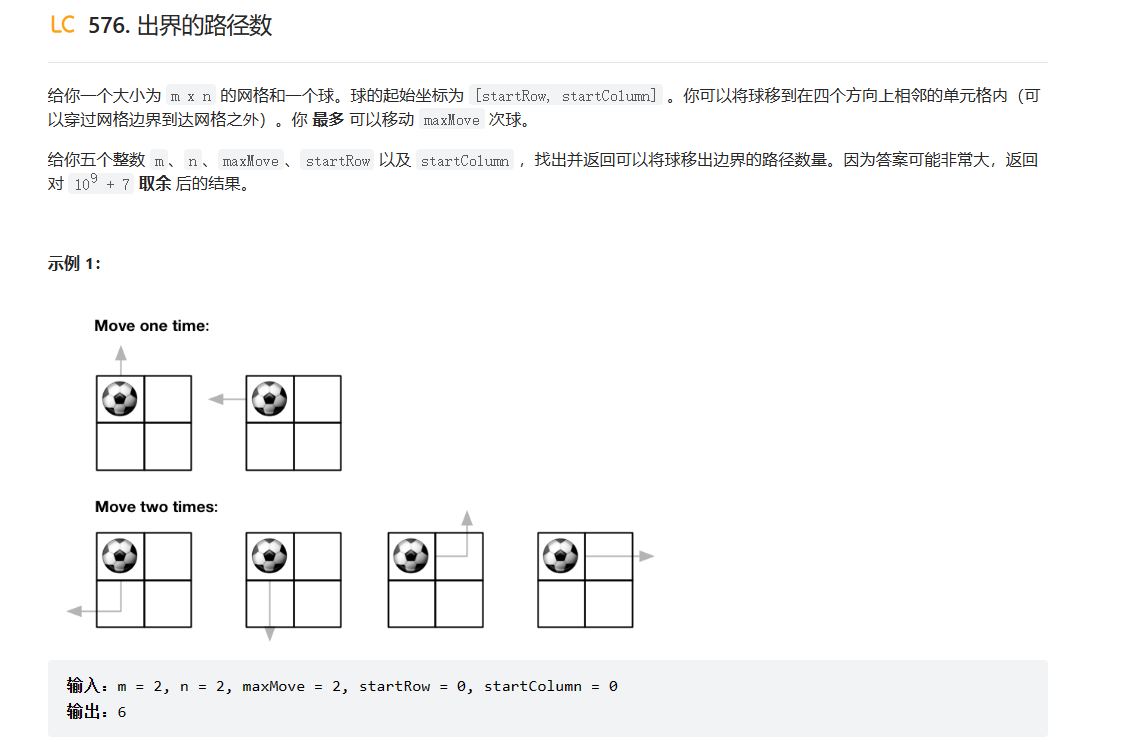
LC576
class Solution {
int MOD=(int)(1e9 + 7);
int[][][] memo;
int m,n;
int[][] dir=new int[][]{{-1,0},{0,1},{1,0},{0,-1}};
public int findPaths(int _m, int _n, int maxMove, int startRow, int startColumn) {

m=_m;
n=_n;
memo=new int[m][n][maxMove+1];

return dp(startRow,startColumn,maxMove);
}
public int dp(int i,int j,int cnt){

if(i<0||i>=m||j<0||j>=n)
return 1;

if(memo[i][j][cnt]!=0)//初始化为0，在图中间会重复计算很多次
return memo[i][j][cnt];
if(cnt<=0)
return 0;
int res=0;
for(int k=0;k<4;k++){
int nx=i+dir[k][0];
int ny=j+dir[k][1];

memo[i][j][cnt]=(memo[i][j][cnt]+dp(nx,ny,cnt-1))%MOD;
}
return memo[i][j][cnt];
}
}
初始化2
class Solution {
int MOD=(int)(1e9 + 7);
int[][][] memo;
int m,n;
int[][] dir=new int[][]{{-1,0},{0,1},{1,0},{0,-1}};
public int findPaths(int _m, int _n, int maxMove, int startRow, int startColumn) {

m=_m;
n=_n;
memo=new int[m][n][maxMove+1];
for(int i=0;i<m;i++)//初始化为-1
for(int j=0;j<n;j++)
for(int k=0;k<=maxMove;k++)
memo[i][j][k]=-1;
return dp(startRow,startColumn,maxMove);
}
public int dp(int i,int j,int cnt){

if(i<0||i>=m||j<0||j>=n)
return 1;

if(memo[i][j][cnt]!=-1)//避免重复计算
return memo[i][j][cnt];
if(cnt<=0)
return 0;
int res=0;
for(int k=0;k<4;k++){
int nx=i+dir[k][0];
int ny=j+dir[k][1];
res=(res+dp(nx,ny,cnt-1))%MOD;
}
return memo[i][j][cnt]=res;
}
}

计数问题能避免很多重复计算