数据结构与算法（25）——二叉查找树BST

• 二叉查找树

性质：比父节点小的key都出现在左子树，比父 节点大的key都出现在右子树。

 

 

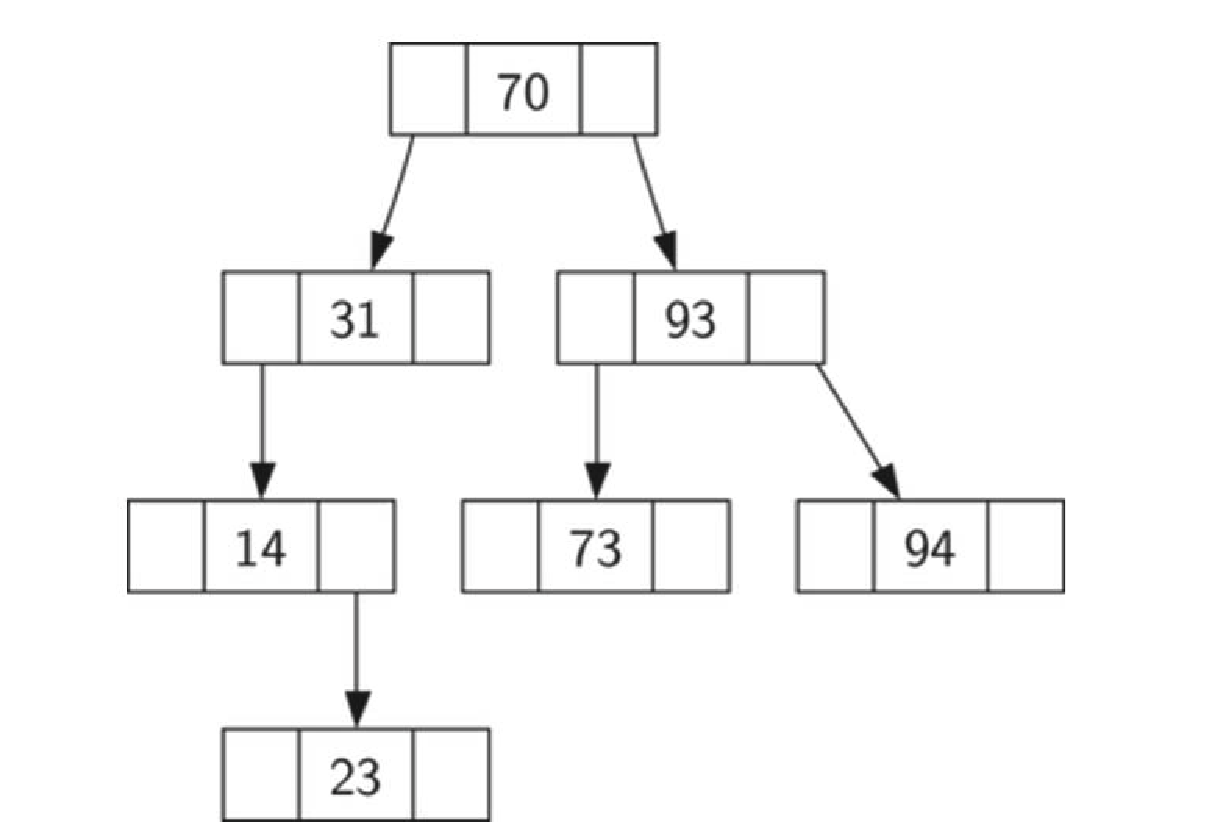
❖按照70,31,93,94,14,23,73的顺序插入

❖首先插入的70成为树根 31比70小，

放到左子节点 93比70大，

放到右子节点 94比93大，

放到右子节点 14比31小，

放到左子节点 23比14大，

放到其右 73比93小，

放到其左

❖注意：插入顺序不同，生成的BST也不同

• 代码实现

class BinarySearchTree:

    def __init__(self):
        self.root = None
        self.size = 0

    def length(self):
        return self.size

    def __len__(self):
        return self.size

    def __iter__(self):
        return self.root.__iter__()

class TreeNode:
    def __init__(self, key, val, left=None, right = None, parent = None):
        self.key = key
        self.payload = val #键值
        self.leftChild = left
        self.rightChild = right
        self.parent = parent

    def hasLeftChild(self):
        return self.leftChild

    def hasRightChild(self):
        return self.rightChild

    def isLeftChild(self):
        return self.parent and self.parent.leftChild == self

    def isRightChild(self):
        return self.parent and self.parent.rightChild == self

    def isRoot(self):
        return not self.parent

    def hasAnyChildren(self):
        return self.rightChild or self.leftChild

    def hasBothChild(self):
        return self.rightChild and self.leftChild

    def replaceNodeData(self,key, value, lc, rc):
        self.key = key
        self.payload = value
        self.leftChild = lc
        self.rightChild = rc
        if self.hasLeftChild():
            self.leftChild.parent = self
        if self.hasRightChild():
            self.rightChild.parent = self
    def put(self, key, val): #插入key构造BST
        if self.root:
            self._put(key, val, self.root)
        else:
            self.root = TreeNode(key, val)
        self.size = self.size + 1
    def _put(self, key, val, currentNode):
        '''
        如果key比currentNode小，那么_put到左子树
        但如果没有左子树，那么key就成为左子节点
        如果key比currentNode大，那么_put到右子树
        但如果没有右子树，那么key就成为右子节点
        '''
        if key < currentNode.key:
            if currentNode.hasLeftChild():
                self._put(key, val, currentNode.leftChild)
            else:
                currentNode.leftChild = TreeNode(key, val, parent=currentNode)
        else:
            if currentNode.hasRightChild():
                self._put(key, val, currentNode.rightChild)
            else:
                currentNode.rightChild = TreeNode(key, val, parent=currentNode)
    def __setitem__(self, k, v):
        self.put(k ,v)

    def get(self, key):
        '''
        在树中找到key所在的节点取到payload
        '''
        if self.root:
            res = self._get(key, self.root)
            if res:
                return res.payloadd
            else:
                return None
        else:
            return None

    def __get(self, key, currentNode):
        if not currentNode:
            return None
        elif currentNode.key == key:
            return currentNode
        elif key < currentNode.key:
            return self.__get(key, currentNode.leftChild)
        else:
            return self.__get(key, currentNode.rightChild)

    def __getitem__(self, key):
        '''
        实现val= myZipTree['PKU']
        '''
        return self.get(key)

    def __contains__(self, key):
        '''
        实现'PKU' in myZipTree的归属判断运算符in
        '''
        if self.__get(key, self.root):
            return True
        else:
            return False
    def __iter__(self):
        '''
        实现迭代器
        迭代器函数中用了for迭代，实际上是递归函数
        yield是对每次迭代的返回值 中序遍历的迭代
        :return:
        '''
        if self:
            if self.hasLeftChild():
                for elem in self.leftChild:
                    yield elem
            yield self.key
            if self.hasRightChild():
                for elem in self.rightChild:
                    yield elem

还有BST.delete方法，BST.remove方法 ，比较复杂，这里就不写了。主要思路是要考虑delete是左子节点还是右子节点，然后是否还有左子节点和右子节点。