数据结构与算法（22）——树

树是一种基本的“非线性”数据结构。基本术语

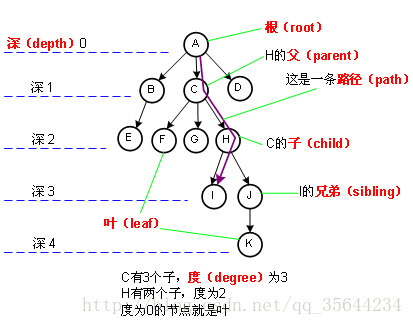
节点Node

边Edge

度：结点拥有的子树数目，如上图结点A的度为3，结点E的度为0

树的度：各个结点中度的最大值

根Root：树中唯一一个没有入边的节点

路径Path：由边依次连接在一起的节点有序表

子节点Children：入边均来自同一个节点的若干节点

父节点Paren：一个节点是其所有边所连接节点的父节点。

兄弟节点Sibling：具有同一个父节点的节点之间的节点称为兄弟节点。

子树Subtree：一个节点和其所有子孙节点，以及相关边的集合。

叶节点Leaf：没有子节点的节点称为叶节点（度为0的结点（没有子树的结点））

层级Level：从根节点开始到达一个节点的路径，所包含的边的数量，称为这个节点的层级。如下图D的层级为2，根节点的层级为0

高度（深度）：树中所有节点的最大层级称为树的高度，如下图所示树的高度为2

二叉树：其中一个节点被设定为根；每个节点n(除根节点)，都恰连接一条来自节点p的边，p是n的父节点；每个节点从根开始的路径是唯一的，如果每个节点最多有两个子节点，这样的树称为“二叉树”

二叉树的性质

二叉树的性质

在二叉树的第i层，至多有2^(i-1)个结点
深度为k的二叉树至多有：(2^k)-1个结点，其实这个结果就是一个等比数列的求和得到的。
对任意一颗二叉树，如果其叶子结点数量为：n0,度为2的结点数为：n2，则：n0=n2+1

证明：这里对第三个性质做一个解释，首先我们都知道一个二叉树每个结点都是由度为0，1，2，三种情况，这里假设，二叉树有n个结点，其中度为1的结点数为：n1，于是由已知条件可知：n=n1+n0+n2;
另外一个角度想，二叉树有B条边，假设这些边都是从父亲结点指向它的孩子，那么会发现除了根结点外，其他结点都是有一条边的，

所以：n=B+1,其中这些边都是由度为1和2的结点射出来的，

所以：B=n1+2*n2,因此：n=n1+2*n2+1.

所以，联立等式：n1+2*n2+1=n1+n0+n2,

我们可以得到一个等式：n0=n2+1;

具有n个结点的完全二叉树的深度为：[log2n]+1，其中[log2n]+1是向下取整。

证明：首先先定义满二叉树：一颗深度为k且结点数为：（2^k）-1的二叉树，称为满二叉树，然后，对满二叉树进行编号，从根结点开始，从左往右，从上到下。

然后可以定义一个完全二叉树：深度为k，结点数为n的二叉树，而且，每一个结点的位置都和深度为k的完全二叉树中编号为1到n的结点一一对应，我们称为完全二叉树。

如下图所示：

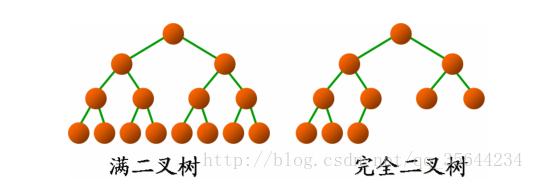
可以解释第四个性质，假设深度为k，由完全二叉树的定义，可以知

道：2^(k-1)-1< n <=(2^k)-1 即：2^(k-1)<=n<(2^k)，所以：k-1 < = [log2n] < k,因为k是整数，所以k=[log2n]+1，其中[log2n]+1是向下取整。

有N个结点的完全二叉树各结点如果用顺序方式存储，则结点之间有如下关系：
　若i为结点编号则如果i>1，则其父结点的编号为[i/2]，[i/2]是往下取整的；
　如果2i<=N，则其左儿子（即左子树的根结点）的编号为2i；若2i>N，则无左儿子；
　如果2i+1<=N，则其右儿子的结点编号为2i+1；若2i+1>N，则无右儿子。

树的应用

文件系统、HTML文档(嵌套标记)、域名体系。

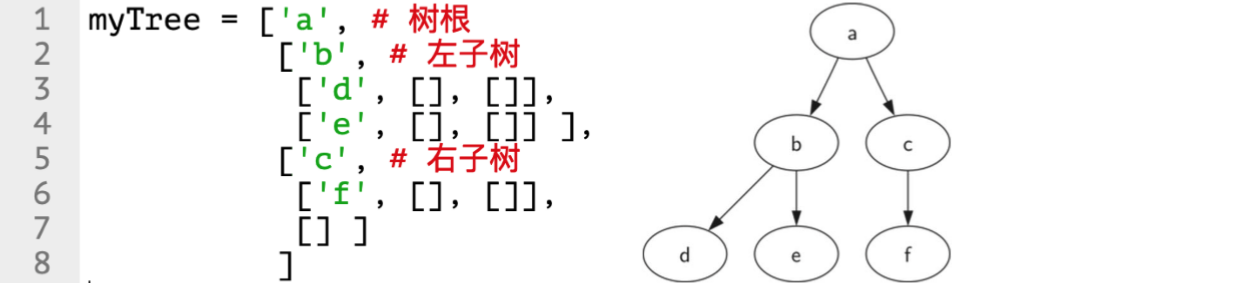
实现树：嵌套列表法

以右图的示例，一个6节点的二叉树根是myTree[0]，左子树myTree[1]，右子树 myTree[2] 。

嵌套列表法的优点子树的结构与树相同，是一种递归数据结构很容易扩展到多叉树，仅需要增加列表元素即可

函数定义：

BinaryTree创建仅有根节点的二叉树

insertLeft/insertRight将新节点插入树中作为其直接的左/右子节点

get/setRootVal则取得或返回根节点

getLeft/RightChild返回左/右子树

#树的嵌套实现
def BinaryTree(r):
    return [r, [], []]

def insertLeft(root, newBranch):
    t = root.pop(1)
    if len(t) > 1:
        root.insert(1, [newBranch,t,[]])
    else:
        root.insert(1,[newBranch,[],[]])
    return root

def insertRight(root, newBranch):
    t = root.pop(2)
    if len(t) > 1:
        root.insert(2, [newBranch,[], t])
    else:
        root.insert(2,[newBranch,[],[]])
    return root
def grtRootVal(root):
    return root[0]

def setRootVal(root, newVal):
    root[0] = newVal
def getLeftChild(root):
    return root[1]
def getRightChild(root):
    return root[2]
r = BinaryTree(3)
insertLeft(r, 4)
insertLeft(r, 5)
insertRight(r,6)
insertRight(r,7)
l = getLeftChild(r)
rl = getRightChild(r)
print("line1:", l)
print("right line:", rl)
print("root line:", r)

setRootVal(l, 9)
print("line2:", r)
print("left sub tree:", getLeftChild(l))
insertLeft(l, 11)
print("line3:",r)
print(getRightChild(getRightChild(r)))

输出

line1: [5, [4, [], []], []]
right line: [7, [], [6, [], []]]
root line: [3, [5, [4, [], []], []], [7, [], [6, [], []]]]
line2: [3, [9, [4, [], []], []], [7, [], [6, [], []]]]
left sub tree: [4, [], []]
line3: [3, [9, [11, [4, [], []], []], []], [7, [], [6, [], []]]]
[6, [], []]

Process finished with exit code 0

实现树：节点链接法

成员key保存根节点数据项

成员left/rightChild则保存指向左/右子树的引用（同样是BinaryTree对象）

二叉树的前序、中序、后序遍历：

前序遍历（DRL）
（1）先访问根结点
（2）先序遍历左子树
（3）先序遍历右子树
中序遍历（LDR）
（1）先中序遍历左子树
（2）访问根结点
（3）中序遍历右子树
后序遍历（LRD）
（1）后序遍历左子树
（2）后序遍历右子树
（3）访问根结点

class BinaryTree:
    def __init__(self, rootObj):
        self.key = rootObj
        self.leftChild = None
        self.rightChild = None

    def insertLeft(self, newNode):
        if self.leftChild == None:
            self.leftChild = BinaryTree(newNode)
        else:
            #这里不是很理解，类似链表的操作，添加左子节点需要将待添加的左子节点指向原来的左子节点
            t = BinaryTree(newNode)
            t.leftChild = self.leftChild
            self.leftChild = t

    def insertRight(self, newNode):
        if self.rightChild == None:
            self.rightChild = BinaryTree(newNode)
        else:
            t = BinaryTree(newNode)
            t.rightChild = self.rightChild
            self.rightChild = t
    def getRightChild(self):
        return self.rightChild

    def getLeftChild(self):
        return self.leftChild

    def setRootVal(self, obj):
        self.key = obj

    def getRootVal(self):
        return self.key

    def preorder(self):
        #前序遍历
        print(self.key)
        if self.leftChild:
            self.leftChild.preorder()
        if self.rightChild:
            self.rightChild.preorder()

    def postorder(self):
        #后序遍历
        if self.leftChild:
            self.leftChild.postorder()
        if self.rightChild:
            self.rightChild.postorder()
        print(self.key)

    def inorder(self):
        #中序遍历
        if self.leftChild:
            self.leftChild.inorder()
　　　　　print(self.key)
        if self.rightChild:
            self.rightChild.inorder()

参考链接：https://blog.csdn.net/qq_35644234/article/details/53013738

posted @ 2020-07-24 14:48 Yelush 阅读(384) 评论(0) 编辑收藏举报

刷新页面返回顶部

Yelush

数据结构与算法（22）——树

公告