【论文阅读】CrossFormer: A Versatile Vision Transformer Based on Cross-scale Attention
来自CVPR 2021
代码地址:https://github.com/cheerss/CrossFormer
一、Motivation
主要还是ViT的历史遗留问题
ViT在处理输入时,将图片划分为了相等大小的图像块(Patch),然后通过linear操作生成token序列,这种操作导致ViT各层的输入嵌入是等尺度的,没有跨尺度特征,缺少不同尺度的交互能力,而这种能力对于视觉感知非常重要。一幅图像通常包含许多不同尺度的对象,建立它们之间的关系需要跨尺度的注意机制。此外,一些任务,如实例分割,需要大规模(粗粒度)特征和小规模(细粒度)特征之间的交互。
现有的vision transformers无法处理这些情况的原因有两个:
(1)嵌入序列是由大小相等的块生成的,因此同一层中的嵌入只具有单一尺度的特征。虽然理论上只要这些patch的大小足够大,可以有机会提取任何尺度的特征,但是patch大小变大后,输出的特征图的分辨率就会变低,难以学习到高分辨率的表征,这对密集预测类的任务很重要;
(2)在Self-Attention模块内部,部分方法放弃了K和V的部分表达,相邻嵌入的键/值经常被合并,以降低成本。因此,即使嵌入同时具有小尺度和大尺度特征,合并操作也会丢失每个单个嵌入的小尺度(细粒度)特征,从而使跨尺度注意力失效。例如,Swin-Transformer将self-attention操作的范围限制在每个window内,这一定程度上放弃了全局尺度的长距离关系。
二、Contribution
这篇文章主要是解决以往架构在建立跨尺度注意力方面的问题,从两个角度提出了跨尺度嵌入层(CEL)和长短距离注意力机制(LDA和SDA)来弥补这方面的空白。
最后附赠一个动态位置偏差(DPB),这与跨尺度无关,通过将偏差添加到注意力机制中表示嵌入的相对位置,动态得到位置偏差可以使相对位置偏差更加灵活。
三、CrossFormer

和PVT、Swin-Transformer一样,CrossFormer也采用了金字塔式的层级的结构,这样的好处是可以迁移到dense任务上去,做检测,分割等。模型分为四个阶段。每个阶段由一个跨尺度嵌入层(CEL)和几个CrossFormer block组成。CEL接收上一阶段的输出(或图像)作为输入,并生成跨尺度嵌入。在这个过程中,CEL(第一阶段除外)将金字塔结构的嵌入次数减少到四分之一,而将其维数增加了一倍。然后,在CEL之后放置几个CrossFormer块(包含LSDA和DPB)。在特定任务的最后阶段之后,紧随其后的是专门的head函数做分类。
1. Cross-scale Embedding Layer (CEL)
CrossFormer是层级的结构,既然是层级的结构那就一定会包含着一定尺度的下采样,这一点PVT和Swin中都有提到,CEL采用不同大小的卷积核(4×4,8×8)对图片做卷积,得到卷积后的结果,直接concat作为Patch Embedding。通过这种方式,强迫一些维度(例如4×4的卷积得到的部分)关注更细粒度、更小尺度的信息,而其他的维度(例如8×8的卷积得到的部分)有机会学习到更大尺度的信息。通过不同大小的卷积核获得不同尺度的信息,对变化尺度的物体是比较友好的。
从图中可以看出,CEL接受一幅影像作为输入,然后使用四个不同大小的卷积核进行采样,四个卷积核的步长大小相同,保证他们生成的token数目相同,四个对应的Patch的中心是相同的,但是尺度不同,将得到的四个尺度的Patch进行concat,就完成了patch embedding。
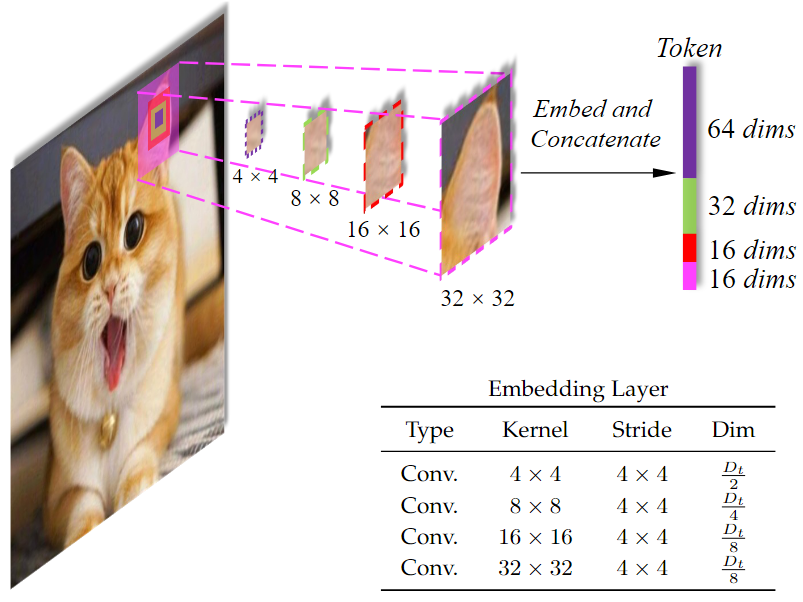
对于跨尺度的嵌入,有一个问题要注意:怎么设置每个尺度的嵌入维度?
先在这里推理一下卷积的计算量(FLOPs )和参数量(Parametaers):
FLOPs:
卷积层计算量 = 卷积矩阵操作 + 融合操作 + bias操作(注意:其中矩阵操作包括:先乘法,再加法)
假设我们输入一张7*7*3的图像,使用大小为5*5*3的84个卷积核,进行stride=1,padding=0的卷积操作,输出3*3*64的feature map
输出图像大小=【(7-5+2*0)/1】+1=3
对于单个像素点来说:需要进行(5*5*3)次卷积矩阵乘法操作,需要进行3*(5*5-1)次卷积矩阵加法操作,(3-1)次通道融合操作,归纳偏置项为1,FLOPs=所有项相加=150
对于一整张feature map有3*3*64个这样的像素点:FLOPs=150*3*3*64=86400
Parameters:
卷积层的参数量只与卷积核有关,Parameters=卷积核计算量+bias
单个卷积核的参数量为5*5*3=75,bias=1,单个卷积核的参数量=75+1=76,一次卷积的Parametars=76*64=4800
从上方推导可以看出,卷积层的计算预算与卷积核大小核输入输出维度有关,假设将每个尺度都设置成相同的维度,那么大的卷积核的计算成本将远大于小的卷积核,为了控制计算成本,所以将较小卷积核设置为较大的维度。
核心代码如下:
- 初始化几个不同kernel,不同padding,相同stride的conv
- 对输入进行卷积操作后得到的feature,做concat
class PatchEmbed(nn.Module):
def __init__(self, img_size=224, patch_size=[4], in_chans=3, embed_dim=96, norm_layer=None):
super().__init__()
...
self.projs = nn.ModuleList()
for i, ps in enumerate(patch_size):
if i == len(patch_size) - 1:
dim = embed_dim // 2 ** i
else:
dim = embed_dim // 2 ** (i + 1)
stride = patch_size[0]
padding = (ps - patch_size[0]) // 2
self.projs.append(nn.Conv2d(in_chans, dim, kernel_size=ps, stride=stride, padding=padding))
if norm_layer is not None:
self.norm = norm_layer(embed_dim)
else:
self.norm = None
def forward(self, x):
B, C, H, W = x.shape
# FIXME look at relaxing size constraints
assert H == self.img_size[0] and W == self.img_size[1], \
f"Input image size ({H}*{W}) doesn't match model ({self.img_size[0]}*{self.img_size[1]})."
xs = []
for i in range(len(self.projs)):
tx = self.projs[i](x).flatten(2).transpose(1, 2)
xs.append(tx) # B Ph*Pw C
x = torch
