【论文阅读】Pyramid Vision Transformer: A Versatile Backbone for Dense Prediction without Convolutions
来自ICCV2021
代码地址:https://github.com/whai362/PVT
一、Motivation
1.将金字塔结构引入视觉Transformer,使视觉Transformer更适应密集预测性的任务;
(金字塔结构:feature map的尺寸随网络的加深逐渐减小,feature map的维度随着网络的加深逐渐增大)
2.设计一个干净的、无卷积的骨干网络代替CNN;
3.ViT的历史遗留问题。
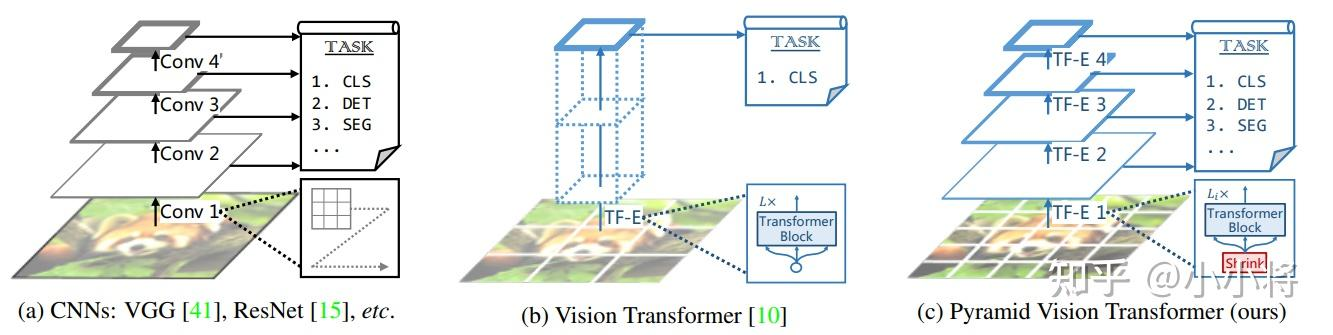
ViT与最原始的Transformer一样,是一个柱状的结构,这意味着它只能全程输出单一尺寸和低分辨率的特征图,ViT的特征图大小,取决于输入端切割图片设置的大小,然而,不同类别、不同任务对于分辨率的需求是不同的,越复杂的图片、越复杂的任务对分辨率的需求就越高,ViT直接采用较大patchs进行token化,如采用16x16大小那么得到的粗粒度特征,对密集任务来说损失较大;另外,一旦输入的图片分辨率变大,占用的显存和计算量就会很大,对于分类任务来说,224×224的分辨率可能足够,但是对于语义分割、目标检测这类任务,需要的分辨率往往较高,占用的显存就非常大。
二、Contribution
1.为了克服传统ViT得到粗粒度特征这个弊端,PVT将细粒度的图像块(4×4)作为输入,学习更高分辨率的表征,这对密集预测性的任务非常重要;
2.随着网络的加深,提出了一个渐进式收缩的金字塔结构,逐步地缩短序列的长度,降低计算成本;
3.将多头自注意力替换为空间缩减自注意力,进一步降低计算资源的消耗。
三、Feature Pyramid Transformer
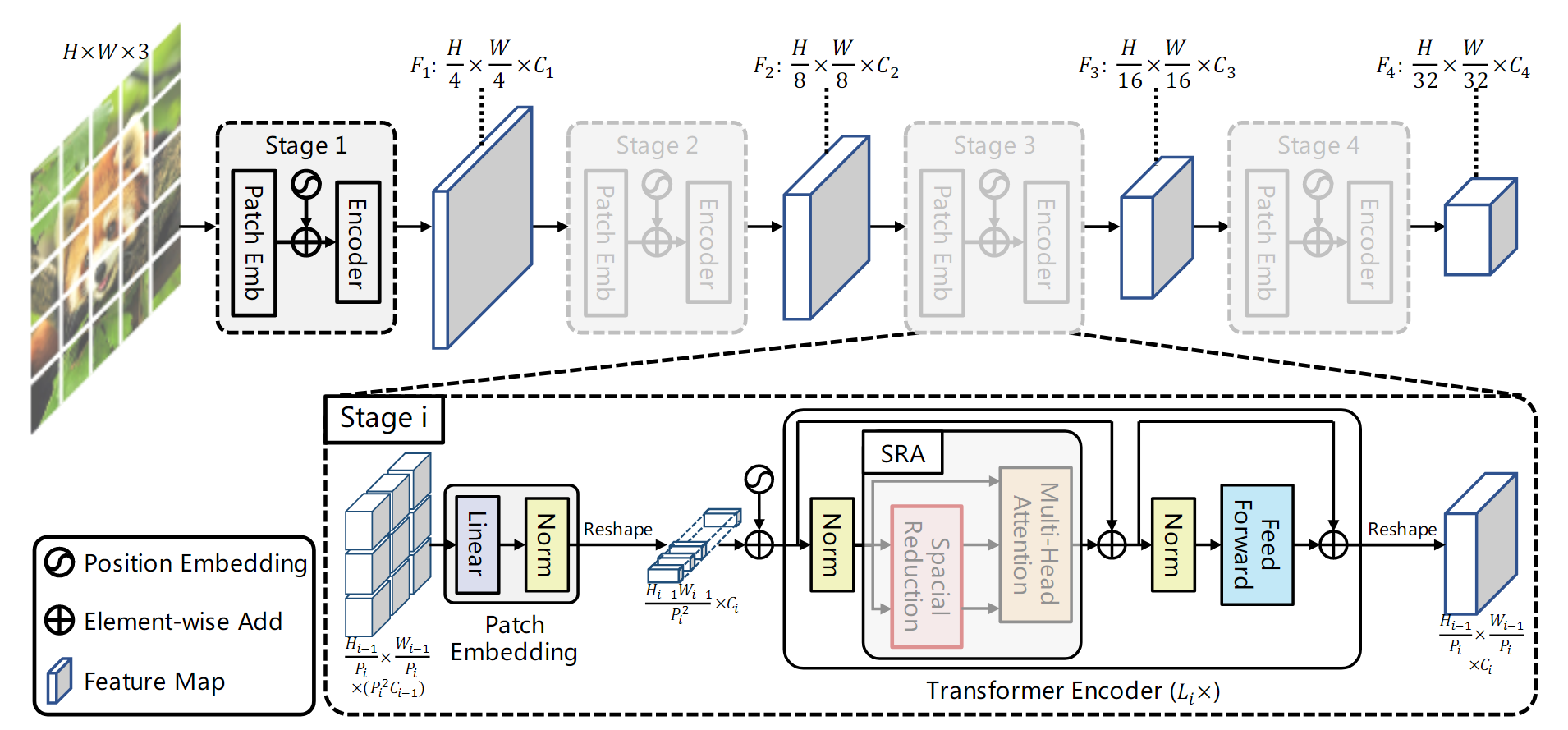
简单地堆叠多个独立的Transformer encoder,采用四个阶段 Transformer 编码器,每个阶段只有参数不同,结构都一样。
在每个stage开始,首先像ViT一样对输入图像进行token化,即进行patch embedding,patch大小均采用2x2大小(第1个stage的patch大小是4x4),这意味着该stage最终得到的特征图维度是减半的,tokens数量对应减少4倍。PVT共4个stage,这和ResNet类似,4个stage得到的特征图相比原图大小分别是1/4,1/8,1/16和1/32。由于不同的stage的tokens数量不一样,所以每个stage采用不同的position embeddings,在patch embed之后加上各自的position embedding,当输入图像大小变化时,position embeddings也可以通过插值来自适应。
不同的stage的tokens数量不同,越靠前的stage的patchs数量越多,我们知道self-attention的计算量与sequence的长度的平方成正比,如果PVT和ViT一样,所有的transformer encoders均采用相同的参数,那么计算量肯定是无法承受的。PVT为了减少计算量,不同的stages采用的网络参数是不同的
为了进一步减少计算量,将常规的multi-head attention (MHA)用spatial-reduction attention (SRA)来替换。SRA的核心是减少attention层的key和value对的数量,常规的MHA在attention层计算时key和value对的数量为sequence的长度,但是SRA将k和V的长度都降低为原来的1/R,计算量减少为原来的1/R²。具体实现代码如下:
class Attention(nn.Module):
def __init__(self, dim, num_heads=8, qkv_bias=False, qk_scale=None, attn_drop=0., proj_drop=0., sr_ratio=1):
super().__init__()
assert dim % num_heads == 0, f"dim {dim} should be divided by num_heads {num_heads}."
self.dim = dim
self.num_heads = num_heads
head_dim = dim // num_heads
self.scale = qk_scale or head_dim ** -0.5
self.q = nn.Linear(dim, dim, bias=qkv_bias)
self.kv = nn.Linear(dim, dim * 2, bias=qkv_bias)
self.attn_drop = nn.Dropout(attn_drop)
self.proj = nn.Linear(dim, dim)
self.proj_drop = nn.Dropout(proj_drop)
self.sr_ratio = sr_ratio
# 实现上这里等价于一个卷积层
if sr_ratio > 1:
self.sr = nn.Conv2d(dim, dim, kernel_size=sr_ratio, stride=sr_ratio)
self.norm = nn.LayerNorm(dim)
def forward(self, x, H, W):
B, N, C = x.shape
q = self.q(x).reshape(B, N, self.num_heads, C // self.num_heads).permute(0, 2, 1, 3)
if self.