二分图详解+题目
前言:
模拟赛是碰到有一道题要用二分图做,写个blog
注意:全文有一些概念要冷静,慢慢琢磨,切勿急躁
介绍
二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。(取自于百度百科)
上面的一段话苦涩难懂,我也是一段时间才看懂
(主要太菜了)
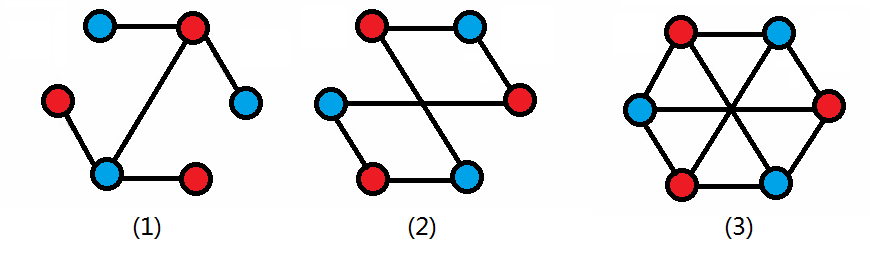
通俗的说 一个无向图中,把所有的点分成两部分(集合),使同一部分(集合)的点不直接相连,不同部分(集合)的点直接相连,这样的图叫做二分图。如图
性质
二分图G的性质是:所有环的长度均为偶数。
不难理解,如上图(2)二分图中有一个环,那么假设起点从点集A(蓝色)出发,那么,经过奇数条边后的点一定在点集B(红色)中,偶数条边后的点一定在点集A(蓝色)中(逆定理亦成立)。又由于环的结尾就是起点,所以边数一定是偶数。
匹配
图论中,一个“匹配”是一个边的集合,其中任意两条都没有公共定点。
如图 两条红线就是这个图的“匹配”之一

最大匹配
求二分图最大匹配可以用最大流或者匈牙利算法。
给定一个二分图G,在G的一个子图M中,M的边集中的任意两条边都不依附于同一个顶点,则称M是一个匹配.
选择这样的边数最大的子集称为图的最大匹配问题(maximal matching problem)
如果一个匹配中,图中的每个顶点都和图中某条边相关联,则称此匹配为完全匹配,也称作完备匹配。
完美匹配:
如果在一个二分图中,存在一个匹配使得所有点都是匹配点,则这个匹配称为这个二分图的完美匹配。可知,一个二分图的完美匹配一定也是这个二分图的一个最大匹配。但并非每个图都存在完美匹配。(不唯一,最大为n!个,可以用dp思想自己算,这里不再赘述)
如图:
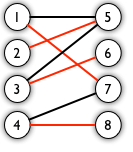
这时就要开始求最大匹配了
算法
求最大匹配的一种显而易见的算法是:先找出全部匹配,然后保留匹配数最多的。但是这个算法的复杂度为边数的指数级函数。因此,需要寻求一种更加高效的算法。
匈牙利算法
这时有个聪明人(匈牙利的Edmonds)发明的一个算法解决了二分图最大匹配问题
这个算法叫作 匈牙利算法。
在学这个算法之前,又要讲讲两个概念——交替路和增广路。
交替路和增广路
交替路:从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。
增广路:从一个未匹配点出法,走交替路,如果途径一个未匹配点(非出发点),则该条交替路称为一个增广路。
用右图举个例子 橙色的是已匹配边和已匹配点,黑色的是未匹配边和未匹配点。
橙色的是已匹配边和已匹配点,黑色的是未匹配边和未匹配点。
如下图是上图的一个增广路展开后的情况

想一想,当我们将橙色和黑色翻转一下,是不是就多了1条匹配的边。因此,我们可以通过不断寻找增广路并将其取反来不断增加匹配中边的数量。等到找不到增广路了,也就说明匹配的边数已经达到最大,即找到了最大匹配。
KM算法
权重问题的转化 / KM算法和匈牙利算法的关系
遇到不会的问题,一个思路就是想办法转换成自己会的问题。我们现在知道匈牙利算法能解决最大匹配的问题,现在加了权重,KM算法实际上就是想了个办法,将问题转换成了匈牙利算法可以解决的形式。所以KM算法解决的是带权二分图的最优匹配问题,而匈牙利算法解决的是二分图的最大匹配。
算法解析
这个KM算法的流程,核心思想就是:优先选择最满意的,因为要求太高找不到对象的那些人,降低标准扩大择偶范围,直到找到对象为止。
这个问题中,找最大匹配的那一部分我们会了呀,用匈牙利算法就搞定了。剩下就是两个问题了:
(1)怎么找到这个所谓的“权重最大的子图”。
(2)怎么扩大择偶范围。既不能降得太低,也不能不降。
上述两个问题,就是KM算法的精髓。
知识点
在实现之前,先了解一下相等子图。
什么是相等子图呢?
每个顶点有一个顶标,如果我们选择边权等于两端点的顶标之和的边,它们组成的图称为相等子图。
这个之后会慢慢理解
模拟
对于像我这种蒟蒻,只能用模拟理解。全程画技粗劣,见谅!
如图是一个带权二分图。

KM算法解决此题的步骤如下所示:
1.首先对每个顶点赋值,将左边的顶点赋值为最大权重,右边的顶点赋值为0。
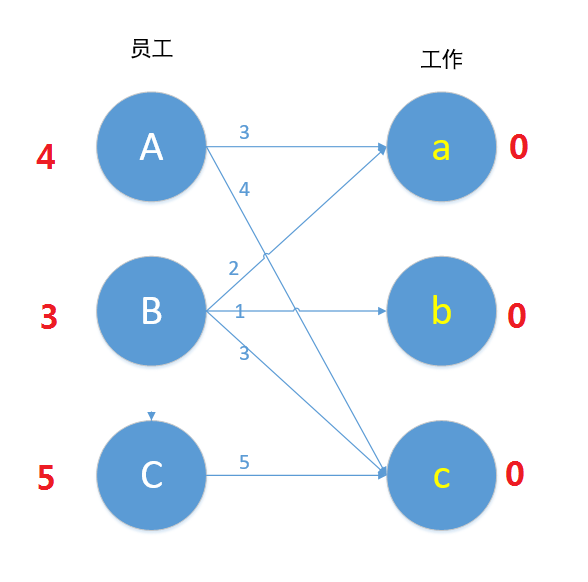
2.进行匹配,我们匹配的原则是:只与边的两个顶点的顶标之和与权重相同的边匹配,若是找不到边匹配,对此条路径的所有左边顶点-1,右边顶点+1,再进行匹配,若还是匹配不到,重复+1和-1操作。(这里看不懂可以跳过,直接看下面的操作,之后再回头来看这里。)
对A进行匹配,符合匹配条件的边只有Ac边。连接Ac。

接下来我们对B进行匹配,顶点B值为3,Bc边权重为3
等等,A已经匹配c了,发生了冲突,怎么办?我们这时候第一时间应该想到的是,让B换个工作,但根据匹配原则,只有Bc边 3+0=3 满足要求,于是B不能换边了,那A能不能换边呢?对A来说,也是只有Ac边满足4+0=4的要求,于是A也不能换边,走投无路了,怎么办?

从常识的角度思考:其实我们寻找最优匹配的过程,也就是帮每个员工找到他们工作效率最高的工作,但是,有些工作会冲突,比如现在,B员工和A员工工作c的效率都是最高,这时我们应该让A或者B换一份工作,但是这时候换工作的话我们只能换到降低总体效率值的工作,也就是说,如果令R=左边顶点所有值相加,若发生了冲突,则最终工作效率一定小于R,但是,我们现在只要求最优匹配,所以,如果A换一份工作降低的工作效率比较少的话,我们是能接受的(对B同样如此)。
在KM算法中如何体现呢?
现在参与到这个冲突的顶点是A,B和c,令所有左边顶点值-1,右边顶点值+1,即 A-1,B-1. c+1(和上文照应),结果如下图所示。
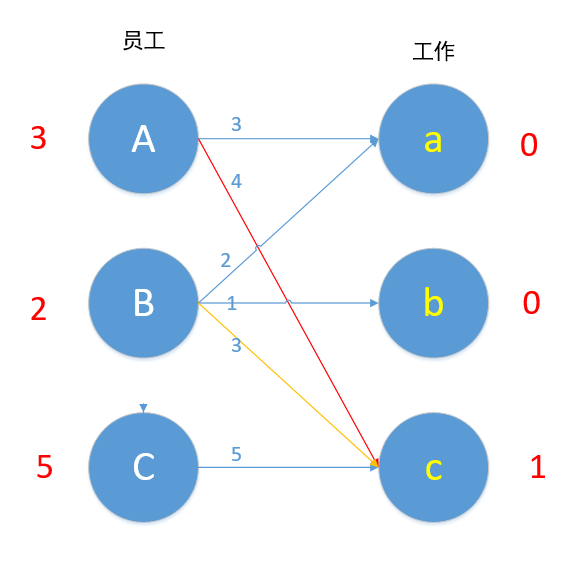
我们进行了上述操作后会发现,Ac本来为可匹配的边,现在仍为可匹配边(3+1=4),对于B来说,Bc本来为可匹配的边,现在仍为可匹配的边(2+1=3),我们通过上述操作,为A增加了一条可匹配的边Aa,为B增加了一条可匹配的边Ba。
现在我们再来匹配,对B来说,Ba边 2+0=2,满足条件,所以B换边,a现在为未匹配状态,Ba匹配!(也可能是Aa匹配Bc匹配,看程序写法,都是最优的→_→)
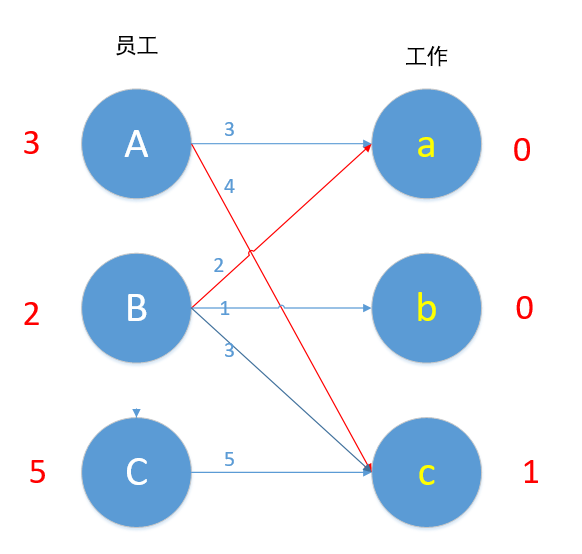
我们现在匹配最后一条边C,Cc 5+1!=5,C边无边能匹配,所以C-1。

现在Cc边 4+1=5,可以匹配,但是c已匹配了,发生冲突,C此时不能换边,于是便去找A,对于A来说,Aa此时也为可匹配边,但是a已匹配,A又去找B。B现在无边可以匹配了,2+0!=1 ,现在的路径是C→c→A→a→B,所以A-1,B-1,C-1,a+1,c+1。如下图所示。
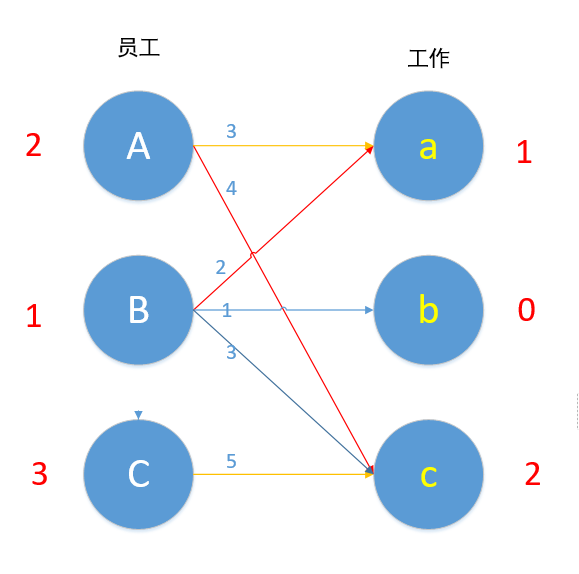
对于B来说,现在Bb 1+0=1 可匹配!再使用匈牙利算法,对此条路径上的边取反。最后如图

如图,便完成了此题的最优匹配。
读者可以发现,这题中冲突一共发生了3次,所以我们一共降低了3次效率值,但是我们每次降低的效率值都是最少的,所以我们完成的仍然是最优匹配!
这就是KM算法的整个过程,整体思路就是:每次都帮一个顶点匹配最大权重边,利用匈牙利算法完成最大匹配,最终我们完成的就是最优匹配!
题目
P3386 【模板】二分图最大匹配
一个十分经典的二分图最大匹配问题
所以用匈牙利算法
算法步骤:
1.把所有点设为非匹配点,S=空集,所有边都是非匹配边。
2.寻找增广路,把路径上所有边状态取反,得到更大匹配Si。
3,重复2步,直到不存在增广路。
找增广路的过程:
枚举左部点x,枚举其连接的右部点y,若y为匹配,由于x为匹配,则构成了长度为1的增广路。
若y匹配,则枚举y连接的所有左部点,做同样的操作,直到找到一个非匹配点。若找不到,则从x出发无法构成增广路。
代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 100005;
int head[N],cnt;
int match[1010];
int vis[1010];
int n,m,e,ans;
struct node{
int to,next;
}edge[N];
void add(int x,int y)
{
edge[++cnt].next=head[x];
edge[cnt].to=y;
head[x]=cnt;
}
bool dfs(int x)
{
for(int i=head[x];i;i=edge[i].next)
{
int y=edge[i].to;
if(vis[y]==0)
{
vis[y]=1;
if(match[y]==0||dfs(match[y])==true)
{
match[y]=x;
return true;
}
}
}
return false;
}
int main()
{
cnt=0;
scanf("%d%d%d",&n,&m,&e);
for(int i=1;i<=e;i++)
{
int u,v;
cin>>u>>v;
v+=n;
add(u,v),add(v,u);
}
ans=0;
for(int i=1;i<=n;i++)
{
memset(vis,0,sizeof(vis));
if(dfs(i)==true)ans++;
}
printf("%d",ans);
return 0;
}
P1894 [USACO4.2]完美的牛栏The Perfect Stall
非常显然,跟模板题差不多,就改了一下输入方式
我这道题和下一道题是一起刷的,改了几行就过了。。。。
#include <bits/stdc++.h>
#define N 405
using namespace std;
int n,cnt,m;
int a[N][N],head[N*N];
bool vis[N];
int match[N];
struct node{
int next,to;
}e[N*N];
int ans;
void add(int x,int y){
e[++cnt].next=head[x];
e[cnt].to=y;
head[x]=cnt;
}
bool dfs(int u){
int v;
for (int i=head[u];i;i=e[i].next){
v=e[i].to;
if (!vis[v]){
vis[v]=1;
if (!match[v]||dfs(match[v])){
match[v]=u;
return true;
}
}
}
return false;
}
int main(){
cnt=0;
ans=0;
memset(e,0,sizeof(e));
memset(head,0,sizeof(head));
memset(match,0,sizeof(match));
scanf("%d%d",&n,&m);
int s1,t;
for (int i=1;i<=n;i++){
scanf("%d",&s1);
for (int j=1;j<=s1;j++){
scanf("%d",&t);
add(i,n+t);
}
}
for (int i=1;i<=n;i++){
memset(vis,0,sizeof(vis));
if (dfs(i))ans++;
}
printf("%d\n",ans);
return 0;
}
P1129 [ZJOI2007] 矩阵游戏
刚看到有点懵,看了题解想到可以把行和列当成二分图的两个集合用链式前向星存入。然后再用匈牙利算法找最大匹配,如果最大匹配是完美匹配,就 \(Yes\) 否则 \(No\)
#include <bits/stdc++.h>
#define N 405
using namespace std;
int n,cnt;
int T;
int a[N][N],head[N*N];
bool vis[N];
int match[N];
struct node{
int next,to;
}e[N*N];
int ans;
void add(int x,int y){
e[++cnt].next=head[x];
e[cnt].to=y;
head[x]=cnt;
}
bool dfs(int u){
int v;
for (int i=head[u];i;i=e[i].next){
v=e[i].to;
if (!vis[v]){
vis[v]=1;
if (!match[v]||dfs(match[v])){
match[v]=u;
return true;
}
}
}
return false;
}
int main(){
scanf("%d",&T);
for (int l=1;l<=T;l++){
cnt=0;
ans=0;
memset(e,0,sizeof(e));
memset(head,0,sizeof(head));
memset(match,0,sizeof(match));
scanf("%d",&n);
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++){
scanf("%d",&a[i][j]);
if (a[i][j])
add(i,j+n);
}
for (int i=1;i<=n;i++){
memset(vis,0,sizeof(vis));
if (dfs(i))ans++;
}
if (ans==n) printf("Yes\n");
else printf("No\n");
}
return 0;
}
P1330 封锁阳光大学
直接黑白染色即可,思维难度并不高。
直接上代码,注释很详细
#include<bits/stdc++.h>
using namespace std;
int n,m,ans,vis[10005],a[2];
int head[10005],k=1,u,v;
struct edge
{
int to,next;
}e[200005];
void adde(int u,int v)//链式前向星
{
e[k].to=v;
e[k].next=head[u];
head[u]=k++;
}
bool dfs(int u,int co)
{
if(vis[u]!=-1)//遍历过了
{
if(vis[u]==co)return 1;//如果已染的色与当前颜色相同,说明可行
return 0;//否则不行
}
vis[u]=co;a[co]++;//标记并统计
bool can=1;
for(register int i=head[u];i&&can;i=e[i].next)
{
int v=e[i].to;
can=can&&dfs(v,!co);//如果仍合法则继续
}
return can;
}
int main()
{
memset(vis,-1,sizeof(vis));//初始化为未染色
scanf("%d%d",&n,&m);
for(register int i=1;i<=m;i++)
{
scanf("%d%d",&u,&v);
adde(u,v);
adde(v,u);
}
for(register int i=1;i<=n;i++)
{
if(vis[i]!=-1)continue;//遍历过则跳过
a[1]=a[0]=0;//初始化这一部分子图所需的黑白数
if(!dfs(i,0)){puts("Impossible");return 0;}
ans+=min(a[1],a[0]);//统计答案,取黑色和白色中较少的那个
}
printf("%d\n",ans);
return 0;
}
P6577 【模板】二分图最大权完美匹配
显然KM算法,于是我直接一发
#include <bits/stdc++.h>
#define INF 1e+7
#define LL long long
using namespace std;
LL n,m;
bool visx[505],visy[505];
int s,t;
int px[505],py[505];
LL wx[505],wy[505];
LL minn;
LL dis[505][505];
LL ans;
bool dfs(int u){
visx[u]=1;
for (int k=1;k<=n;k++){
if (!visy[k]){
LL t=wx[u]+wy[k]-dis[u][k];
if (t==0){
visy[k]=1;
if (!py[k]||dfs(py[k])){
px[u]=k;py[k]=u;
return true;
}
}else if (t>0){
minn=min(minn,t);
}
}
}
return false;
}
int main(){
memset(wx,-0x7f,sizeof(wx));
memset(wy,0,sizeof(wy));
memset(px,0,sizeof(px));
memset(py,0,sizeof(py));
scanf("%lld%lld",&n,&m);
for (int i=1;i<=m;i++){
scanf("%d%d",&s,&t);
scanf("%lld",&dis[s][t]);
wx[s]=max(wx[s],dis[s][t]);
}
for (int i=1;i<=n;i++){
while (1){
minn=INF;
memset(visx,0,sizeof(visx));
memset(visy,0,sizeof(visy));
if (dfs(i))break;
for (int j=1;j<=n;j++){
if (visx) wx[j]-=minn;
if (visy) wy[j]+=minn;
}
}
}
ans=0;
for (int i=1;i<=n;i++)
ans+=(long long)wx[i]+(long long)wy[i];
printf("%lld\n",ans);
for (int i=1;i<=n;i++)
printf("%d ",py[i]);
return 0;
}
好家伙,结果发现就对了一个其他全TLE,虽然是KM算法模板题,但是出题人故意卡我们。
我们简单分析一下复杂度:
-
每次扩大相等子图最少只能加入一条相等边,也就是最多会进行\(n^2\)次扩大相等子图。
-
每次扩大相等子图后都需要进行dfs増广,单次复杂度可达\(n^2\)。
也就是说,km+dfs的复杂度完全可以卡到\(n^4\)
这时需要考虑如何优化,我们不难发现每次扩大相等子图之后,都要从増广起点重新开始dfs,这个过程是有明显的时间浪费的。能不能在扩大相等子图之后,保留上次状态呢?
答案是可行的,我们只需要换用bfs写法:在每次扩大子图后,都记录一下新加入的相等边所为我们提供的新増广方向,然后从此处继续寻找増广路即可。
扩大相等子图复杂度:
- 每次扩大相等子图最少只能加入一条相等边,也就是最多会进行\(n^2\)次扩大相等子图。
- 每次扩大相等子图复杂度n,无需额外増广,从上次起点继续増广即可。
増广复杂度:
- 每个左部点需要1次増广,共有n个左部点。
单次増广复杂度可达\(n^2\)。
由此可见,通过简单的状态延续策略,我们成功将km算法的复杂度降到了\(n^3\)。
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
typedef long long ll;
const ll Maxn=505;
const ll inf=1e18;
ll n,m,map[Maxn][Maxn],matched[Maxn];
ll slack[Maxn],pre[Maxn],ex[Maxn],ey[Maxn];
bool visx[Maxn],visy[Maxn];
void match(ll u)
{
ll x,y=0,yy=0,delta;
memset(pre,0,sizeof(pre));
for(ll i=1;i<=n;i++)slack[i]=inf;
matched[y]=u;
while(1)
{
x=matched[y];delta=inf;visy[y]=1;
for(ll i=1;i<=n;i++)
{
if(visy[i])continue;
if(slack[i]>ex[x]+ey[i]-map[x][i])
{
slack[i]=ex[x]+ey[i]-map[x][i];
pre[i]=y;
}
if(slack[i]<delta){delta=slack[i];yy=i;}
}
for(ll i=0;i<=n;i++)
{
if(visy[i])ex[matched[i]]-=delta,ey[i]+=delta;
else slack[i]-=delta;
}
y=yy;
if(matched[y]==-1)break;
}
while(y){matched[y]=matched[pre[y]];y=pre[y];}
}
ll KM()
{
memset(matched,-1,sizeof(matched));
memset(ex,0,sizeof(ex));
memset(ey,0,sizeof(ey));
for(ll i=1;i<=n;i++)
{
memset(visy,0,sizeof(visy));
match(i);
}
ll res=0;
for(ll i=1;i<=n;i++)
if(matched[i]!=-1)res+=map[matched[i]][i];
return res;
}
int main()
{
ll u,v,w;
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
map[i][j]=-inf;
for(ll i=1;i<=m;i++)
{
scanf("%lld%lld%lld",&u,&v,&w);
map[u][v]=w;
}
printf("%lld\n",KM());
for(ll i=1;i<=n;i++)
printf("%lld ",matched[i]);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号