C++笔记(5)——浮点数的比较
判断是否相等
因为一个浮点数的存储并不总是精确的,例如在经过大量计算之后可能会将3.14保存为3.1400000000001或者3.1439999999999,这时候如果直接用==来比较这两个数的话会输出错误的结果,false(C++中==只有在两个数字完全相同的情况下才判定为true)。所以需要引入极小数eps来修正,只要不超出这个误差,那么就判定为true。
通常定义一个eps为常量1e-8:
const double eps = 1e-8;
对应的定义判定是否相等的操作Equ:
#define Equ(a, b) ((fabs((a)-(b))<(eps))
上面这行代码是通过宏定义来定义出一个名为Equ的函数,这个函数会将a和b相减,如果相差的结果的绝对值小于极小值eps,那么就判定为true,否则为false。上面加这么多括号是为了防止宏定义可能带来的错误,不能够省略掉。相对应的,如果需要使用不等于,那么只需要用!Equ(a, b)即可。
使用上述函数的例子:
#include <stdio.h>
#include <math.h>
const double eps = 1e-8;
#define Equ(a,b) ((fabs((a) - (b)) < (eps))
int main(){
double db = 1.23;
if(Equ(db, 1.23)){
printf("equal");
}
else{
printf("not equal")
}
return 0;
}
大于
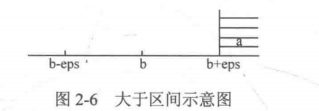
#define More(a,b) (((a) - (b)) > (eps))
小于

#define Less(a,b) (((a)-(b)) < (-eps))
大于等于
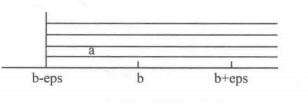
#define MoreEqu(a,b) (((a)-(b))>(-eps))
小于等于

#define LessEqu(a,b) (((a)-(b))<(eps))
补充:圆周率
\(\cos{\pi} = -1\), \(\pi = \arccos{-1}\),所以:
const double Pi = acos(-1.0);
与误差相关的补充
另外还有:
- 在经过大量计算后可能因为误差的累计,一个变量中存储的0实际上是一个非常小的负数,如果这时候对这个变量进行开根号操作
sqrt,那么会报错(asin(x)类似,当存放的x为+1或-1时也会出现类似的情况)。因此需要用eps来保证变量在定义域内; - 一些编译环境下0.00的变量可能在输出时会变成-0.00。这是一个bug,只能将结果放在字符串中然后和-0.00比较,如果对比成功那么将结果加上eps来变回0.00 。
参考
《算法笔记》胡凡著
本博客文章默认使用CC BY-SA 3.0协议。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号