BST学习笔记

序言

本文的作者是在不知道STL直接提供了可用的BST下学习的BST，所以嫌麻烦的话可以直接使用STL（逃）

概念

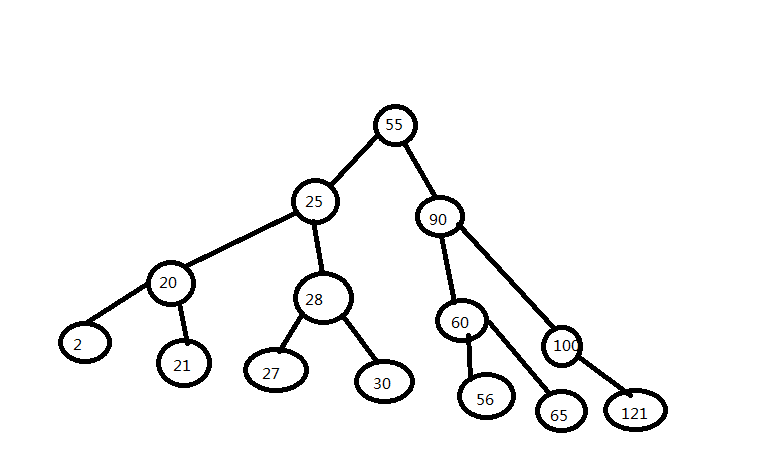
二叉搜索树BST(binary search tree)是一颗二叉树，它的每个内部节点都关联一个关键字，并具有以下性质：任意节点的关键字大于（或等于）该节点左子树中所有节点的关键字，小于（或等于）该节点右子树中所有节点的关键字。简单的来说，就是一个点的权值小于等于右儿子子树所有点的权值，大于等于左儿子子树所有点的权值。如下图：

用途

插入
删除x
查询x
查询排名为x
求
求

实现

定义：

struct BST{
    int son[2],fa,val,num,siz;//son[2]左右儿子，fa父亲，val权值，num这个点权值出现的次数，siz子树大小
    inline void init(int v,int f)//权值和父亲
    {
        val=v;
        fa=f;
        num=siz=1;
        son[0]=son[1]=0;
    } 
}t[N];

一些用到的小函数：

inline int judge(int x)//判断x是其父亲的哪一个儿子 
{
    return t[t[x].fa].son[1]==x;
}
inline void update(int x)//x为根的树有多少值 
{
    t[x].siz=t[x].num+t[t[x].son[0]].siz+t[t[x].son[1]].siz;//因为一个值可能出现多次，我们用一个点就可以了
}
inline void merge(int x,int y,int opt)//x成为y的儿子 
{
    t[x].fa=y;
    t[y].son[opt]=x;
}

插入操作：

inline void insert(int v,int f,int n)
{
    if(!n)//如果这个v值没有出现过，就新增一个节点 
    {
        t[++cnt].init(v,f);
        merge(cnt,f,v>t[f].val);
        if(n==rt) rt=cnt; //这一步是为了在son为空时，让第一个插入的点成为根,否则rt一直都是0 
           return ;
    }
    t[n].siz++;
    if(t[n].val==v) {t[n].num++;return ;}
    if(t[n].val>v) insert(v,n,t[n].son[0]);
    else insert(v,n,t[n].son[1]);
}

查询编号：

inline int find(int v,int n)//查询某个值对应的节点编号
{
    if(!n) return -1;
    if(t[n].val==v) return n;
    if(t[n].val>v) return find(v,t[n].son[0]);
    else return find(v,t[n].son[1]);
}

查询一个值的前驱后继：

inline int find_pre(int v,int n,int ans)//查询前驱 
{
    if(!n) return ans;
    if(t[n].val>=v) return find_pre(v,t[n].son[0],ans);
    else return find_pre(v,t[n].son[1],t[n].val);
}
inline int find_suf(int v,int n,int ans)//查询后继 
{
    if(!n) return ans;
    if(t[n].val<=v) return find_suf(v,t[n].son[1],ans);
    else return find_suf(v,t[n].son[0],t[n].val);
}

删点（准确来说是删掉一个值）：

inline void crash(int v)//删除一个权值为V的点 
{
    int n=find(v,rt);
    if(!n) return ;
    if(t[n].num>1){t[n].num--;return ;}
    if(!t[n].son[0]&&!t[n].son[1]){t[t[n].fa].son[judge(n)]=0;return ;}
    if(!t[n].son[0]||!t[n].son[1])
    {
        if(n==rt) rt=0;
        t[t[n].son[0]+t[n].son[1]].fa=t[n].fa;
        t[t[n].fa].son[judge(n)]=t[n].son[0]+t[n].son[1];
        return ;
    }
    int pos=find_pre(t[n].val,n,0);
    swap(t[n].val,t[pos].val);
    t[t[pos].fa].son[judge(pos)]=0; 
}

用值找排名和用排名找值：

inline int v_rank(int v,int n,int ans)//用值找排名 
{
    if(t[n].val==v) return ans+t[t[n].son[0]].siz+1;
    if(t[n].val>v) return v_rank(v,t[n].son[0],ans);
    else return v_rank(v,t[n].son[1],ans+t[t[n].son[0]].siz+t[n].num);
}
inline int rank_v(int rank,int n)//用排名找值 
{
    if(t[t[n].son[0]].siz>rank) return rank_v(rank,t[n].son[0]);
    if(t[t[n].son[0]].siz+t[n].num<rank)
    return rank_v(rank-t[t[n].son[0]].siz-t[n].num,t[n].son[1]);
    return t[n].val;
}

最后贴一下完整代码，（按照洛谷P3369题意，如果不怕T可以提交）

#include<bits/stdc++.h>
const int N=1e6+5;
using namespace std;
int cnt,rt;
struct BST{
    int son[2],fa,val,num,siz;//son[2]左右儿子，fa父亲，val权值，num这个点权值出现的次数，siz子树大小
    inline void init(int v,int f)//权值和父亲
    {
        val=v;
        fa=f;
        num=siz=1;
        son[0]=son[1]=0;
    } 
}t[N]; 
inline int judge(int x)//判断x是其父亲的哪一个儿子 
{
    return t[t[x].fa].son[1]==x;
}
inline void update(int x)//x为根的树有多少值 
{
    t[x].siz=t[x].num+t[t[x].son[0]].siz+t[t[x].son[1]].siz;
}
inline void merge(int x,int y,int opt)//x成为y的儿子 
{
    t[x].fa=y;
    t[y].son[opt]=x;
} 
inline void insert(int v,int f,int n)
{
    if(!n)//如果这个v值没有出现过，就新增一个节点 
    {
        t[++cnt].init(v,f);
        merge(cnt,f,v>t[f].val);
        if(n==rt) rt=cnt; //这一步是为了在son为空时，让第一个插入的点成为根,否则rt一直都是0 
           return ;
    }
    t[n].siz++;
    if(t[n].val==v) {t[n].num++;return ;}
    if(t[n].val>v) insert(v,n,t[n].son[0]);
    else insert(v,n,t[n].son[1]);
}
inline int find(int v,int n)//查询某个值对应的节点编号
{
    if(!n) return -1;
    if(t[n].val==v) return n;
    if(t[n].val>v) return find(v,t[n].son[0]);
    else return find(v,t[n].son[1]);
}
inline int find_pre(int v,int n,int ans)//查询前驱 
{
    if(!n) return ans;
    if(t[n].val>=v) return find_pre(v,t[n].son[0],ans);
    else return find_pre(v,t[n].son[1],t[n].val);
}
inline int find_suf(int v,int n,int ans)//查询后继 
{
    if(!n) return ans;
    if(t[n].val<=v) return find_suf(v,t[n].son[1],ans);
    else return find_suf(v,t[n].son[0],t[n].val);
}
inline void crash(int v)//删除一个权值为V的点 
{
    int n=find(v,rt);
    if(!n) return ;
    if(t[n].num>1){t[n].num--;return ;}
    if(!t[n].son[0]&&!t[n].son[1]){t[t[n].fa].son[judge(n)]=0;return ;}
    if(!t[n].son[0]||!t[n].son[1])
    {
        if(n==rt) rt=0;
        t[t[n].son[0]+t[n].son[1]].fa=t[n].fa;
        t[t[n].fa].son[judge(n)]=t[n].son[0]+t[n].son[1];
        return ;
    }
    int pos=find_pre(t[n].val,n,0);
    swap(t[n].val,t[pos].val);
    t[t[pos].fa].son[judge(pos)]=0; 
}
inline int v_rank(int v,int n,int ans)//用值找排名 
{
    if(t[n].val==v) return ans+t[t[n].son[0]].siz+1;
    if(t[n].val>v) return v_rank(v,t[n].son[0],ans);
    else return v_rank(v,t[n].son[1],ans+t[t[n].son[0]].siz+t[n].num);
}
inline int rank_v(int rank,int n)//用排名找值 
{
    if(t[t[n].son[0]].siz>rank) return rank_v(rank,t[n].son[0]);
    if(t[t[n].son[0]].siz+t[n].num<rank)
    return rank_v(rank-t[t[n].son[0]].siz-t[n].num,t[n].son[1]);
    return t[n].val;
}
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch>'9' || ch<'0'){if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int main()
{
    int n,q;
    n=read();
    while(n--)
    {
        q=read();
        if(q==1) insert(read(),0,rt);
        if(q==2) crash(read());
        if(q==3) printf("%d\n",v_rank(read(),rt,0));
        if(q==4) printf("%d\n",rank_v(read(),rt));
        if(q==5) printf("%d\n",find_pre(read(),rt,0));
        if(q==6) printf("%d\n",find_suf(read(),rt,0));
    }
    return 0; 
}

其他

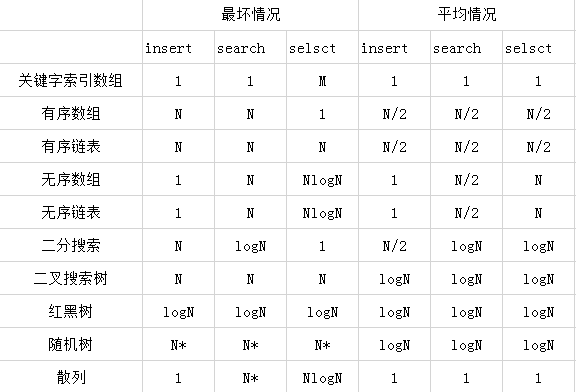
二叉搜索树在最坏情况下insert操作是N，search操作是N，select操作也是N，平均都是logN。（我在想二分搜索在最坏情况下都比它跑的快），我们在这里可以与其他方式进行时间复杂度对比：

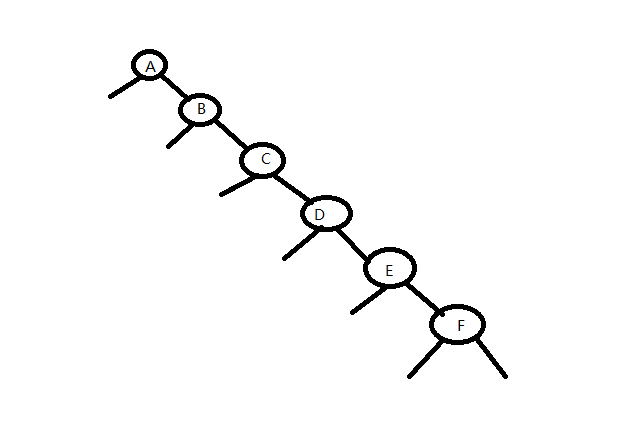
以及毒瘤出题人的两种毒瘤数据：

posted @ 2019-08-03 17:22 sooner 阅读(234) 评论(0) 编辑收藏举报

刷新页面返回顶部

avogadro

BST学习笔记