DS博客作业02--栈和队列
0.PTA得分截图

1.本周学习总结
1.1总结栈和队列内容
栈的存储结构
顺序栈

链栈

顺序栈的基本操作
栈的结构体
typedef Struct
{
ElemType data[MaxSize];
int top;//栈顶指针
} Stack;
typedef Stack *SqStack;
初始化栈
void InitStack(SqQtack &s)
{
s=new Stack;
栈顶指针指向-1;
}
销毁栈
void DestoryStack(SqStack &s)
{
delete s;
}
判断空栈
bool StackEmpty(SqStack s)
{
return(栈顶指针=-1);
}
入栈
bool Push(SqStack &s,ElemType e)
{
if(栈满)
return false;
栈顶指针增1;
将e给栈顶指针元素赋值;
return true;
}
出栈
bool Pop(SqStack &s,ElemType &e)
{
if(栈空)
returen false;
取栈顶指针元素赋值给e;
栈顶指针减1;
return true;
}
取栈顶元素
bool GetTop(SqStack *s,ElemType &e)
{
if(栈空)
return false;
将栈顶元素赋值给e;
return true;
}
栈的应用
中缀表达式转后缀表达式,测试题中出现过的进制转换,括号匹配,浏览器回退功能等。
队列的存储结构
顺序队列
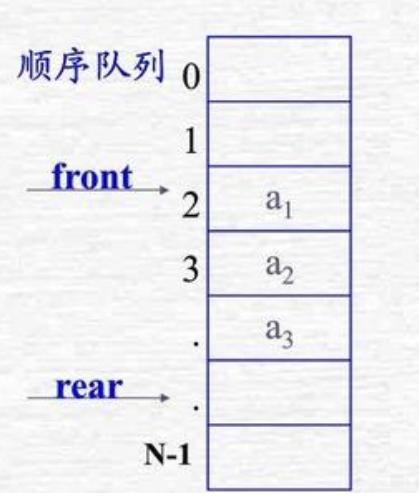
链队列
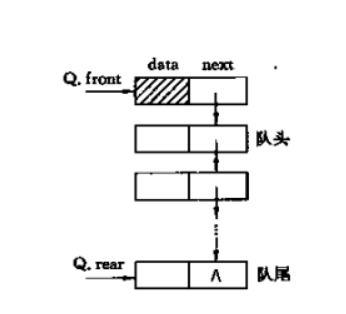
队列的基本操作
队列的结构体
typedef struct Queue
{
ElementType *Data;
int front; //队头指针
int rear; //队尾指针
}SqQueue;
初始化队列
void InitQueue(Queue &Q)
{
队头指针=-1;
队尾指针=-1;
}
判断空队列
bool EmptyQueue(Queue &Q)
{
if(Q->front==Q->rear)//队空的判断条件
{
return true;
}
else
{
return false;
}
}
入队列
入队列
bool EnQueue(Queue &Q,int e)
{
if(队满)
return false;
队尾指针增1;
将e赋值给队尾指针元素;
return true;
}
出队列
出队列
bool DeQueue(Queue &Q)
{
if(队空)
return false;
队头指针增1
return true;
}
循环队列
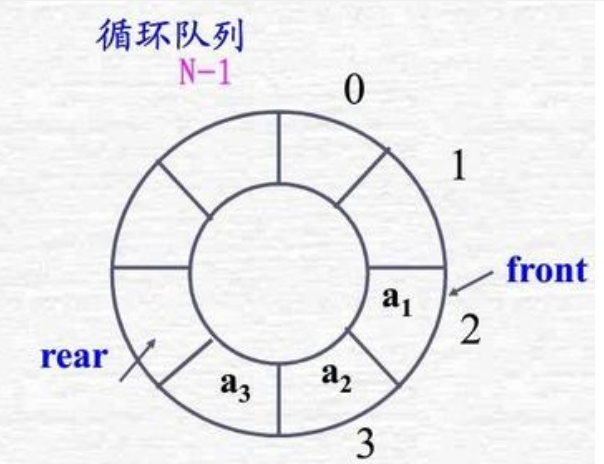
循环队列的结构体
循环队列的存储结构
typedef struct SqQueue
{
int data[MAXSIZE];
int front;
int rear;
}SQueue;
循环队列入队
void EnQueue(Queue& Q,int e)
{
if((Q->rear+1)%Q->maxsize==Q->front)//队列已满
return false;
Q->rear=(Q->rear+1)%Q->maxsize;
将e赋值给队尾指针元素;
}
循环队列出队
void DeQueue(Queue& Q)
{
if(Q->front==Q->rear)//队空
return false;
Q->front=(Q->front+1)%maxsize;
}
队列的应用
现在我知道的队列的应用主要是在处理生活中的排队问题,如PTA中的银行排队问题,还有就是报数问题。
1.2.谈谈你对栈和队列的认识及学习体会
栈和队列严格意义上来讲都是属于线性表,存储结构上,栈是“先进后出”,而队列是“先进先出”,巧妙利用他们的性质可以解决不同的题目。做栈和队列的PTA题目时,没啥思路时,照着测试点多画图理解就好做多了,比如符号配对和表达式转换。在编程题中,了解到了map函数和string函数的使用,这样让代码简洁了不少。
2.PTA实验作业
2.1 7-3 jmu-ds-符号配对 (15分)
2.1.1 代码截图


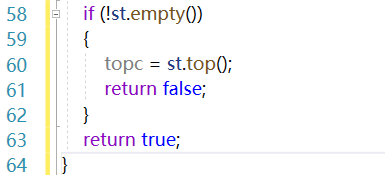
2.1.2本题PTA提交列表说明

Q1:部分正确
A1:一开始没有将栈顶为空即topc=0单独考虑,导致输出时会空一行再输出no;
Q2: 编译错误
A2: 修改的时候直接在PTA上修改,结果改错了一个变量名没发现;
2.2 6-2 在一个数组中实现两个堆栈 (20分)
2.2.1 代码截图


2.2.2本题PTA提交列表说明

Q1: 部分正确
A1:Push函数的第一个==写成了=
Q2: 部分正确
A2:S->Data[--(S->Top2)]=X前多写了一行Top2--,导致前3个测试点一直错。
3.阅读代码
3.1 题目及解题代码

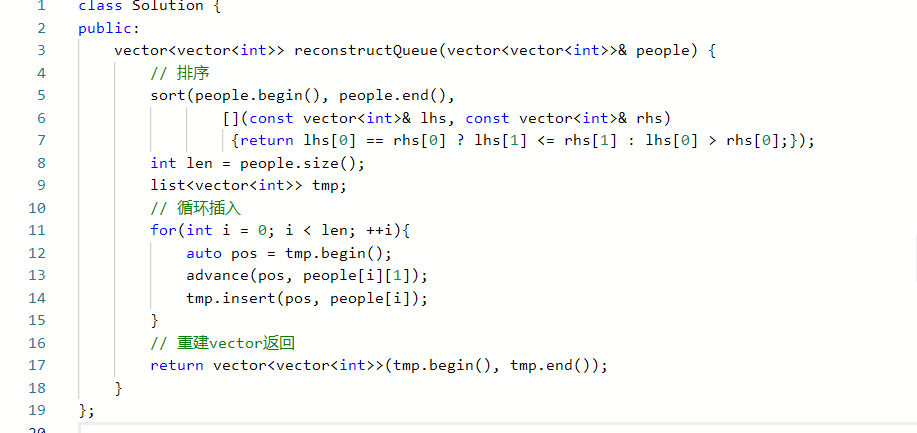
3.1.1 该题的设计思路
·先排身高更高的,这是要防止后排入人员影响先排入人员位置
·每次排入新人员[h,k]时,已处于队列的人身高都>=h,所以新排入位置就是people[k]
时间复杂度O(n),空间复杂度O(n);
3.1.2该题的伪代码
先将people按照身高降序排序,又由于每次插入的位置是k,所以相同身高需要按k升序排序,否则插入位置会越界
list<vector<int>> tmp;//使用list作为中间容器
for(i=0;i<people.size;++i)
{
循环地从头读取people
据people[i][1]也就是k,插入list
用advance()找到插入位置
}
将完成地所有插入操作地list重建为vector返回
3.1.3运行结果
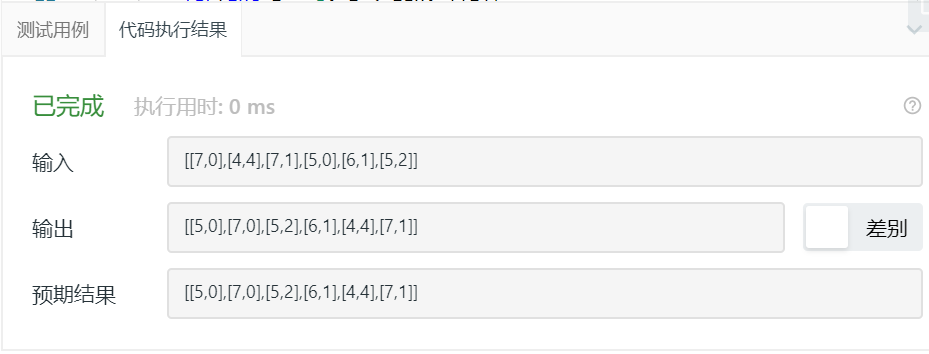
3.1.4分析该题目解题优势及难点。
优势是在由于需要频繁使用insert()操作,而使用了list作为中间容器,减少了代码量。
难点在于要先排身高更高地,不然后排入人员会影响先拍入人员位置以及人数升序排列的预处理。
3.2题目及解题代码
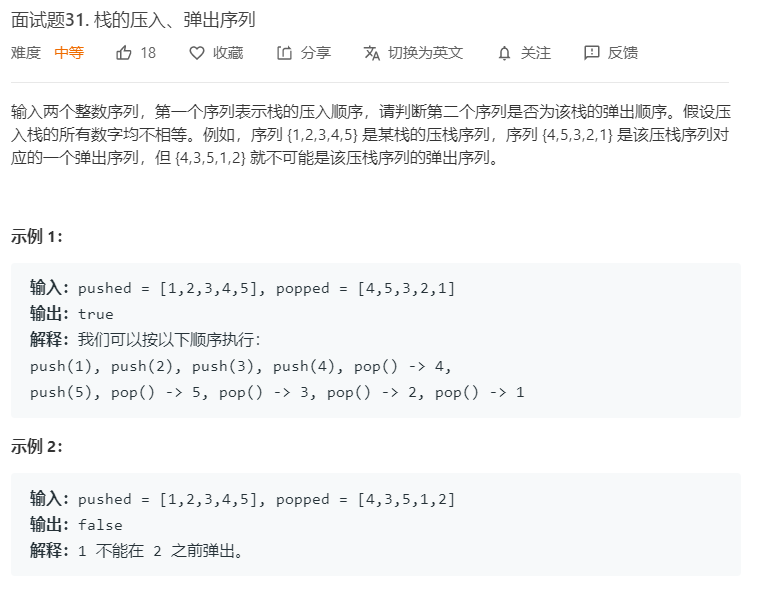

3.2.1该题的设计思路
按照 popped 中的顺序模拟出栈操作,如果符合则返回 true,否则返回 false。这里用到的贪心法则是如果栈顶元素等于 popped 序列中下一个要 pop 的值,则应立刻将该值 pop 出来。
使用一个栈 st 来模拟该操作。将 pushed 数组中的每个数依次入栈,同时判断这个数是不是 popped 数组中下一个要 pop 的值,如果是就把它 pop 出来。最后检查栈是否为空。
时间复杂度O(n),空间复杂度O(n);
3.2.2该题的伪代码
for (int i = 0; i < pushed.size(); ++i)
{
数据进栈;
while(栈不空,未遍历结束,栈顶数据等于popped[j]
{
出栈;
j++;
}
return st.empty();
}
3.2.3运行结果
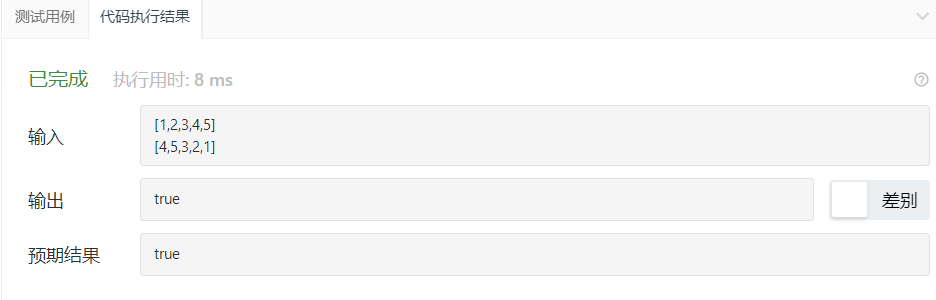
3.2.4分析该题目解题优势及难点。
优势是在算法高效,只要一遍入栈和出栈;
难点是在于联想到使用辅助栈和贪心算法。





