《Java架构师的第一性原理》52算法之labuladong的算法小抄之框架套路

1 原文链接

https://labuladong.gitbook.io/algo-en/v/master

https://labuladong.gitee.io/algo/

2 关键词学习法

数组（顺序存储）、链表（链式存储）

队列、栈、图（邻接表、邻接矩阵）、散列表、树（堆、二叉树、多叉树）

遍历 + 访问、增删查改

所谓框架，就是套路

动态规划问题：「状态转移方程」 + 「最优子结构」+ 「重叠子问题」

3.1 遍历 + 访问套路框架

线性就是 for/while 迭代为代表，非线性就是递归为代表。

1）数组遍历框架，典型的线性迭代结构

void traverse(int[] arr) {
    for (int i = 0; i < arr.length; i++) {
        // 迭代访问 arr[i]
    }
}

2）链表遍历框架，兼具迭代和递归结构

/* 基本的单链表节点 */
class ListNode {
    int val;
    ListNode next;
}

void traverse(ListNode head) {
    for (ListNode p = head; p != null; p = p.next) {
        // 迭代访问 p.val
    }
}

void traverse(ListNode head) {
    // 递归访问 head.val
    traverse(head.next);
}

3）二叉树遍历框架，典型的非线性递归遍历结构

/* 基本的二叉树节点 */
class TreeNode {
    int val;
    TreeNode left, right;
}

void traverse(TreeNode root) {
    traverse(root.left);
    traverse(root.right);
}

4）二叉树框架可以扩展为 N 叉树的遍历框架：

/* 基本的 N 叉树节点 */
class TreeNode {
    int val;
    TreeNode[] children;
}

void traverse(TreeNode root) {
    for (TreeNode child : root.children)
        traverse(child);
}

3.2 动态规划套路框架

状态转移方程：

明确 base case

　　-> 明确「状态」

　　-> 明确「选择」

　　-> 定义 dp 数组/函数的含义。

按上面的套路走，最后的结果就可以套这个框架：

# 初始化 base case
dp[0][0][...] = base
# 进行状态转移
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)

PS：但凡遇到需要递归的问题，最好都画出递归树，这对你分析算法的复杂度，寻找算法低效的原因都有巨大帮助。

递归算法的时间复杂度怎么计算？就是用子问题个数乘以解决一个子问题需要的时间。

1）暴力递归

int fib(int N) {
    if (N == 1 || N == 2) return 1;
    return fib(N - 1) + fib(N - 2);
}

这就是动态规划问题的第一个性质：重叠子问题。

2）带备忘录的递归解法（自顶向下）

 一般使用一个数组充当这个「备忘录」，当然你也可以使用哈希表（字典），思想都是一样的。

实际上，带「备忘录」的递归算法，把一棵存在巨量冗余的递归树通过「剪枝」，改造成了一幅不存在冗余的递归图，极大减少了子问题（即递归图中节点）的个数。

int fib(int N) {
    if (N < 1) return 0;
    // 备忘录全初始化为 0
    vector<int> memo(N + 1, 0);
    // 进行带备忘录的递归
    return helper(memo, N);
}

int helper(vector<int>& memo, int n) {
    // base case
    if (n == 1 || n == 2) return 1;
    // 已经计算过
    if (memo[n] != 0) return memo[n];
    memo[n] = helper(memo, n - 1) + helper(memo, n - 2);
    return memo[n];
}

3）dp数组的迭代解法（自底向上）

int fib(int N) {
    if (N < 1) return 0;
    if (N == 1 || N == 2) return 1;
    vector<int> dp(N + 1, 0);
    // base case
    dp[1] = dp[2] = 1;
    for (int i = 3; i <= N; i++)
        dp[i] = dp[i - 1] + dp[i - 2];
    return dp[N];
}

 

「状态转移方程」：你把 f(n) 想做一个状态 n，这个状态 n 是由状态 n - 1 和状态 n - 2 相加转移而来，这就叫状态转移，仅此而已。

 

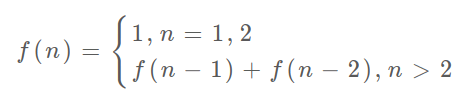
4）解法三的优化「状态压缩」

int fib(int n) {
    if (n < 1) return 0;
    if (n == 2 || n == 1) 
        return 1;
    int prev = 1, curr = 1;
    for (int i = 3; i <= n; i++) {
        int sum = prev + curr;
        prev = curr;
        curr = sum;
    }
    return curr;
}

根据斐波那契数列的状态转移方程，当前状态只和之前的两个状态有关，其实并不需要那么长的一个 DP table 来存储所有的状态，只要想办法存储之前的两个状态就行了。所以，可以进一步优化，把空间复杂度降为 O(1)。

这个技巧就是所谓的「状态压缩」，如果我们发现每次状态转移只需要 DP table 中的一部分，那么可以尝试用状态压缩来缩小 DP table 的大小，只记录必要的数据，上述例子就相当于把DP table 的大小从 n 缩小到 2。后续的动态规划章节中我们还会看到这样的例子，一般来说是把一个二维的 DP table 压缩成一维，即把空间复杂度从 O(n^2) 压缩到 O(n)。

3.3 回溯算法（ DFS 算法）套路框架

回溯算法框架。解决一个回溯问题，实际上就是一个决策树的遍历过程。你只需要思考 3 个问题：

1、路径：也就是已经做出的选择。

2、选择列表：也就是你当前可以做的选择。

3、结束条件：也就是到达决策树底层，无法再做选择的条件。

代码方面，回溯算法的框架：

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

其核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」，特别简单。

我们定义的 backtrack 函数其实就像一个指针，在这棵树上游走，同时要正确维护每个节点的属性，每当走到树的底层，其「路径」就是一个全排列。 

多叉树的遍历框架就是这样：

void traverse(TreeNode root) {
    for (TreeNode child : root.childern)
        // 前序遍历需要的操作
        traverse(child);
        // 后序遍历需要的操作
}

而所谓的前序遍历和后序遍历，他们只是两个很有用的时间点。

前序遍历的代码在进入某一个节点之前的那个时间点执行，后序遍历代码在离开某个节点之后的那个时间点执行。

回溯算法的这段核心框架：

for 选择 in 选择列表:
    # 做选择
    将该选择从选择列表移除
    路径.add(选择)
    backtrack(路径, 选择列表)
    # 撤销选择
    路径.remove(选择)
    将该选择再加入选择列表

必须说明的是，不管怎么优化，都符合回溯框架，而且时间复杂度都不可能低于 O(N!)，因为穷举整棵决策树是无法避免的。这也是回溯算法的一个特点，不像动态规划存在重叠子问题可以优化，回溯算法就是纯暴力穷举，复杂度一般都很高。

3.4 BFS算法套路框架

回溯算法框架。解决一个回溯问题，实际上就是一个决策树的遍历过程。你只需要思考 3 个问题：

BFS 的核心思想应该不难理解的，就是把一些问题抽象成图，从一个点开始，向四周开始扩散。一般来说，我们写 BFS 算法都是用「队列」这种数据结构，每次将一个节点周围的所有节点加入队列。

BFS 相对 DFS 的最主要的区别是：BFS 找到的路径一定是最短的，但代价就是空间复杂度比 DFS 大很多。

让你从一个起点，走到终点，问最短路径。这就是 BFS 的本质，框架搞清楚了直接默写就好。

记住下面这个框架就 OK 了：

// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
    Queue<Node> q; // 核心数据结构
    Set<Node> visited; // 避免走回头路

    q.offer(start); // 将起点加入队列
    visited.add(start);
    int step = 0; // 记录扩散的步数

    while (q not empty) {
        int sz = q.size();
        /* 将当前队列中的所有节点向四周扩散 */
        for (int i = 0; i < sz; i++) {
            Node cur = q.poll();
            /* 划重点：这里判断是否到达终点 */
            if (cur is target)
                return step;
            /* 将 cur 的相邻节点加入队列 */
            for (Node x : cur.adj())
                if (x not in visited) {
                    q.offer(x);
                    visited.add(x);
                }
        }
        /* 划重点：更新步数在这里 */
        step++;
    }
}

1）二叉树的最小高度

int minDepth(TreeNode root) {
    if (root == null) return 0;
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);
    // root 本身就是一层，depth 初始化为 1
    int depth = 1;

    while (!q.isEmpty()) {
        int sz = q.size();
        /* 将当前队列中的所有节点向四周扩散 */
        for (int i = 0; i < sz; i++) {
            TreeNode cur = q.poll();
            /* 判断是否到达终点 */
            if (cur.left == null && cur.right == null) 
                return depth;
            /* 将 cur 的相邻节点加入队列 */
            if (cur.left != null)
                q.offer(cur.left);
            if (cur.right != null) 
                q.offer(cur.right);
        }
        /* 这里增加步数 */
        depth++;
    }
    return depth;
}

形象点说，DFS 是线，BFS 是面；DFS 是单打独斗，BFS 是集体行动。这个应该比较容易理解吧。

BFS 可以找到最短距离，但是空间复杂度高，而 DFS 的空间复杂度较低。

3.5 二分搜索套路框架

二分查找并不简单，Knuth 大佬（发明 KMP 算法的那位）都说二分查找：思路很简单，细节是魔鬼。很多人喜欢拿整型溢出的 bug 说事儿，但是二分查找真正的坑根本就不是那个细节问题，而是在于到底要给 mid 加一还是减一，while 里到底用 <= 还是 <。

二分查找场景：寻找一个数、寻找左侧边界、寻找右侧边界。

1）二分查找框架

int binarySearch(int[] nums, int target) {
    int left = 0, right = ...;

    while(...) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            ...
        } else if (nums[mid] < target) {
            left = ...
        } else if (nums[mid] > target) {
            right = ...
        }
    }
    return ...;
}

分析二分查找的一个技巧是：不要出现 else，而是把所有情况用 else if 写清楚，这样可以清楚地展现所有细节。本文都会使用 else if，旨在讲清楚，读者理解后可自行简化。

2）寻找左侧边界的二分查找

左闭右开的写法

int left_bound(int[] nums, int target) {
    if (nums.length == 0) return -1;
    int left = 0;
    int right = nums.length; // 注意

    while (left < right) { // 注意
        int mid = (left + right) / 2;
        if (nums[mid] == target) {
            right = mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid; // 注意
        }
    }
    return left;
}

两端都闭的「搜索区间」

int left_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    // 搜索区间为 [left, right]
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            // 搜索区间变为 [mid+1, right]
            left = mid + 1;
        } else if (nums[mid] > target) {
            // 搜索区间变为 [left, mid-1]
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 收缩右侧边界
            right = mid - 1;
        }
    }
    // 检查出界情况
    if (left >= nums.length || nums[left] != target)
        return -1;
    return left;
}

3）寻找右侧边界的二分查找

int right_bound(int[] nums, int target) {
    if (nums.length == 0) return -1;
    int left = 0, right = nums.length;

    while (left < right) {
        int mid = (left + right) / 2;
        if (nums[mid] == target) {
            left = mid + 1; // 注意
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid;
        }
    }
    return left - 1; // 注意
}

两端都闭的「搜索区间」

int right_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 这里改成收缩左侧边界即可
            left = mid + 1;
        }
    }
    // 这里改为检查 right 越界的情况，见下图
    if (right < 0 || nums[right] != target)
        return -1;
    return right;
}

4）总结框架

int binary_search(int[] nums, int target) {
    int left = 0, right = nums.length - 1; 
    while(left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1; 
        } else if(nums[mid] == target) {
            // 直接返回
            return mid;
        }
    }
    // 直接返回
    return -1;
}

int left_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 别返回，锁定左侧边界
            right = mid - 1;
        }
    }
    // 最后要检查 left 越界的情况
    if (left >= nums.length || nums[left] != target)
        return -1;
    return left;
}


int right_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 别返回，锁定右侧边界
            left = mid + 1;
        }
    }
    // 最后要检查 right 越界的情况
    if (right < 0 || nums[right] != target)
        return -1;
    return right;
}

3.6 滑动窗口套路框架

1）滑动窗口算法的代码框架

/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;

    int left = 0, right = 0;
    int valid = 0; 
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        // 右移窗口
        right++;
        // 进行窗口内数据的一系列更新
        ...

        /*** debug 输出的位置 ***/
        printf("window: [%d, %d)\n", left, right);
        /********************/

        // 判断左侧窗口是否要收缩
        while (window needs shrink) {
            // d 是将移出窗口的字符
            char d = s[left];
            // 左移窗口
            left++;
            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

2）最小覆盖子串

string minWindow(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;

    int left = 0, right = 0;
    int valid = 0;
    // 记录最小覆盖子串的起始索引及长度
    int start = 0, len = INT_MAX;
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        // 右移窗口
        right++;
        // 进行窗口内数据的一系列更新
        if (need.count(c)) {
            window[c]++;
            if (window[c] == need[c])
                valid++;
        }

        // 判断左侧窗口是否要收缩
        while (valid == need.size()) {
            // 在这里更新最小覆盖子串
            if (right - left < len) {
                start = left;
                len = right - left;
            }
            // d 是将移出窗口的字符
            char d = s[left];
            // 左移窗口
            left++;
            // 进行窗口内数据的一系列更新
            if (need.count(d)) {
                if (window[d] == need[d])
                    valid--;
                window[d]--;
            }                    
        }
    }
    // 返回最小覆盖子串
    return len == INT_MAX ?
        "" : s.substr(start, len);
}

3）字符串排列

// 判断 s 中是否存在 t 的排列
bool checkInclusion(string t, string s) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;

    int left = 0, right = 0;
    int valid = 0;
    while (right < s.size()) {
        char c = s[right];
        right++;
        // 进行窗口内数据的一系列更新
        if (need.count(c)) {
            window[c]++;
            if (window[c] == need[c])
                valid++;
        }

        // 判断左侧窗口是否要收缩
        while (right - left >= t.size()) {
            // 在这里判断是否找到了合法的子串
            if (valid == need.size())
                return true;
            char d = s[left];
            left++;
            // 进行窗口内数据的一系列更新
            if (need.count(d)) {
                if (window[d] == need[d])
                    valid--;
                window[d]--;
            }
        }
    }
    // 未找到符合条件的子串
    return false;
}

4）所有字母异位词

vector<int> findAnagrams(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;

    int left = 0, right = 0;
    int valid = 0;
    vector<int> res; // 记录结果
    while (right < s.size()) {
        char c = s[right];
        right++;
        // 进行窗口内数据的一系列更新
        if (need.count(c)) {
            window[c]++;
            if (window[c] == need[c]) 
                valid++;
        }
        // 判断左侧窗口是否要收缩
        while (right - left >= t.size()) {
            // 当窗口符合条件时，把起始索引加入 res
            if (valid == need.size())
                res.push_back(left);
            char d = s[left];
            left++;
            // 进行窗口内数据的一系列更新
            if (need.count(d)) {
                if (window[d] == need[d])
                    valid--;
                window[d]--;
            }
        }
    }
    return res;
}

5）最长无重复字串

int lengthOfLongestSubstring(string s) {
    unordered_map<char, int> window;

    int left = 0, right = 0;
    int res = 0; // 记录结果
    while (right < s.size()) {
        char c = s[right];
        right++;
        // 进行窗口内数据的一系列更新
        window[c]++;
        // 判断左侧窗口是否要收缩
        while (window[c] > 1) {
            char d = s[left];
            left++;
            // 进行窗口内数据的一系列更新
            window[d]--;
        }
        // 在这里更新答案
        res = max(res, right - left);
    }
    return res;
}

3.7 股票买卖问题（动态规划）

AAA

3.8 打家劫舍问题

BBB

3.9 区间问题

BBB

3.10 nSum问题

1）twoSum问题

使用双指针技巧。

或者一个通用化的 twoSum 函数。

vector<vector<int>> twoSumTarget(vector<int>& nums, int target) {
    // nums 数组必须有序
    sort(nums.begin(), nums.end());
    int lo = 0, hi = nums.size() - 1;
    vector<vector<int>> res;
    while (lo < hi) {
        int sum = nums[lo] + nums[hi];
        int left = nums[lo], right = nums[hi];
        if (sum < target) {
            while (lo < hi && nums[lo] == left) lo++;
        } else if (sum > target) {
            while (lo < hi && nums[hi] == right) hi--;
        } else {
            res.push_back({left, right});
            while (lo < hi && nums[lo] == left) lo++;
            while (lo < hi && nums[hi] == right) hi--;
        }
    }
    return res;
}

2）3Sum问题

4 手把手带你刷链表

4.1 递归反转链表的一部分

对于递归算法，最重要的就是明确递归函数的定义。具体来说，我们的 reverse 函数定义是这样的：

1）递归反转整个链表

ListNode reverse(ListNode head) {
    if (head.next == null) return head;
    ListNode last = reverse(head.next);
    head.next.next = head;
    head.next = null;
    return last;
}

2）反转链表前N个节点

解决思路和反转整个链表差不多，只要稍加修改即可：

ListNode successor = null; // 后驱节点

// 反转以 head 为起点的 n 个节点，返回新的头结点
ListNode reverseN(ListNode head, int n) {
    if (n == 1) { 
        // 记录第 n + 1 个节点
        successor = head.next;
        return head;
    }
    // 以 head.next 为起点，需要反转前 n - 1 个节点
    ListNode last = reverseN(head.next, n - 1);

    head.next.next = head;
    // 让反转之后的 head 节点和后面的节点连起来
    head.next = successor;
    return last;
}

3）反转链表的一部分

ListNode reverseBetween(ListNode head, int m, int n) {
    // base case
    if (m == 1) {
        return reverseN(head, n);
    }
    // 前进到反转的起点触发 base case
    head.next = reverseBetween(head.next, m - 1, n - 1);
    return head;
}

4.2 如果k个一组反转链表

/** 反转区间 [a, b) 的元素，注意是左闭右开 */
ListNode reverse(ListNode a, ListNode b) {
    ListNode pre, cur, nxt;
    pre = null; cur = a; nxt = a;
    // while 终止的条件改一下就行了
    while (cur != b) {
        nxt = cur.next;
        cur.next = pre;
        pre = cur;
        cur = nxt;
    }
    // 返回反转后的头结点
    return pre;
}

ListNode reverseKGroup(ListNode head, int k) {
    if (head == null) return null;
    // 区间 [a, b) 包含 k 个待反转元素
    ListNode a, b;
    a = b = head;
    for (int i = 0; i < k; i++) {
        // 不足 k 个，不需要反转，base case
        if (b == null) return head;
        b = b.next;
    }
    // 反转前 k 个元素
    ListNode newHead = reverse(a, b);
    // 递归反转后续链表并连接起来
    a.next = reverseKGroup(b, k);
    return newHead;
}

4.3 如果判断回文链表

1）判断回文字符串「双指针技巧」

bool isPalindrome(string s) {
    int left = 0, right = s.length - 1;
    while (left < right) {
        if (s[left] != s[right])
            return false;
        left++; right--;
    }
    return true;
}

2）判断回文单链表

最简单的办法就是，把原始链表反转存入一条新的链表，然后比较这两条链表是否相同。关于如何反转链表，可以参见前文「递归操作链表」。

其实，借助二叉树后序遍历的思路，不需要显式反转原始链表也可以倒序遍历链表。

模仿双指针实现回文判断的功能：

// 左侧指针
ListNode left;

boolean isPalindrome(ListNode head) {
    left = head;
    return traverse(head);
}

boolean traverse(ListNode right) {
    if (right == null) return true;
    boolean res = traverse(right.next);
    // 后序遍历代码
    res = res && (right.val == left.val);
    left = left.next;
    return res;
}

优化空间复杂度

ListNode reverse(ListNode head) {
    ListNode pre = null, cur = head;
    while (cur != null) {
        ListNode next = cur.next;
        cur.next = pre;
        pre = cur;
        cur = next;
    }
    return pre;
}

5 手把手带你刷二叉树

所有回溯、动归、分治算法，其实都是树的问题。快速排序就是个二叉树的前序遍历，归并排序就是个二叉树的后序遍历。

而树的问题就永远逃不开树的递归遍历框架这几行破代码：

/* 二叉树遍历框架 */
void traverse(TreeNode root) {
    // 前序遍历
    traverse(root.left)
    // 中序遍历
    traverse(root.right)
    // 后序遍历
}

1）快速排序

void sort(int[] nums, int lo, int hi) {
    /****** 前序遍历位置 ******/
    // 通过交换元素构建分界点 p
    int p = partition(nums, lo, hi);
    /************************/

    sort(nums, lo, p - 1);
    sort(nums, p + 1, hi);
}

2）归并排序

void sort(int[] nums, int lo, int hi) {
    int mid = (lo + hi) / 2;
    sort(nums, lo, mid);
    sort(nums, mid + 1, hi);

    /****** 后序遍历位置 ******/
    // 合并两个排好序的子数组
    merge(nums, lo, mid, hi);
    /************************/
}

3）写递归算法的秘诀

我们前文 二叉树的最近公共祖先 写过，写递归算法的关键是要明确函数的「定义」是什么，然后相信这个定义，利用这个定义推导最终结果，绝不要跳入递归的细节。

计算一棵二叉树共有几个节点：

// 定义：count(root) 返回以 root 为根的树有多少节点
int count(TreeNode root) {
    // base case
    if (root == null) return 0;
    // 自己加上子树的节点数就是整棵树的节点数
    return 1 + count(root.left) + count(root.right);
}

4）翻转二叉树

// 将整棵树的节点翻转
TreeNode invertTree(TreeNode root) {
    // base case
    if (root == null) {
        return null;
    }

    /**** 前序遍历位置 ****/
    // root 节点需要交换它的左右子节点
    TreeNode tmp = root.left;
    root.left = root.right;
    root.right = tmp;

    // 让左右子节点继续翻转它们的子节点
    invertTree(root.left);
    invertTree(root.right);

    return root;
}

首先讲这道题目是想告诉你，二叉树题目的一个难点就是，如何把题目的要求细化成每个节点需要做的事情。

2）填充二叉树节点的右侧指针

回想刚才说的，二叉树的问题难点在于，如何把题目的要求细化成每个节点需要做的事情，但是如果只依赖一个节点的话，肯定是没办法连接「跨父节点」的两个相邻节点的。

那么，我们的做法就是增加函数参数，一个节点做不到，我们就给他安排两个节点，「将每一层二叉树节点连接起来」可以细化成「将每两个相邻节点都连接起来」：

// 主函数
Node connect(Node root) {
    if (root == null) return null;
    connectTwoNode(root.left, root.right);
    return root;
}

// 辅助函数
void connectTwoNode(Node node1, Node node2) {
    if (node1 == null || node2 == null) {
        return;
    }
    /**** 前序遍历位置 ****/
    // 将传入的两个节点连接
    node1.next = node2;

    // 连接相同父节点的两个子节点
    connectTwoNode(node1.left, node1.right);
    connectTwoNode(node2.left, node2.right);
    // 连接跨越父节点的两个子节点
    connectTwoNode(node1.right, node2.left);
}

3）将二叉树展开为链表 

如何按题目要求把一棵树拉平成一条链表？很简单，以下流程：

1、将 root 的左子树和右子树拉平。

2、将 root 的右子树接到左子树下方，然后将整个左子树作为右子树。

// 定义：将以 root 为根的树拉平为链表
void flatten(TreeNode root) {
    // base case
    if (root == null) return;

    flatten(root.left);
    flatten(root.right);

    /**** 后序遍历位置 ****/
    // 1、左右子树已经被拉平成一条链表
    TreeNode left = root.left;
    TreeNode right = root.right;

    // 2、将左子树作为右子树
    root.left = null;
    root.right = left;

    // 3、将原先的右子树接到当前右子树的末端
    TreeNode p = root;
    while (p.right != null) {
        p = p.right;
    }
    p.right = right;
}

4）构造最大二叉树

我们说过写树的算法，关键思路如下：

把题目的要求细化，搞清楚根节点应该做什么，然后剩下的事情抛给前/中/后序的遍历框架就行了，我们千万不要跳进递归的细节里，你的脑袋才能压几个栈呀。

/* 主函数 */
TreeNode constructMaximumBinaryTree(int[] nums) {
    return build(nums, 0, nums.length - 1);
}

/* 将 nums[lo..hi] 构造成符合条件的树，返回根节点 */
TreeNode build(int[] nums, int lo, int hi) {
    // base case
    if (lo > hi) {
        return null;
    }

    // 找到数组中的最大值和对应的索引
    int index = -1, maxVal = Integer.MIN_VALUE;
    for (int i = lo; i <= hi; i++) {
        if (maxVal < nums[i]) {
            index = i;
            maxVal = nums[i];
        }
    }

    TreeNode root = new TreeNode(maxVal);
    // 递归调用构造左右子树
    root.left = build(nums, lo, index - 1);
    root.right = build(nums, index + 1, hi);

    return root;
}

5）通过前序和中序遍历结果构造二叉树

TreeNode build(int[] preorder, int preStart, int preEnd, 
               int[] inorder, int inStart, int inEnd) {

    if (preStart > preEnd) {
        return null;
    }

    // root 节点对应的值就是前序遍历数组的第一个元素
    int rootVal = preorder[preStart];
    // rootVal 在中序遍历数组中的索引
    int index = 0;
    for (int i = inStart; i <= inEnd; i++) {
        if (inorder[i] == rootVal) {
            index = i;
            break;
        }
    }

    int leftSize = index - inStart;

    // 先构造出当前根节点
    TreeNode root = new TreeNode(rootVal);
    // 递归构造左右子树
    root.left = build(preorder, preStart + 1, preStart + leftSize,
                      inorder, inStart, index - 1);

    root.right = build(preorder, preStart + leftSize + 1, preEnd,
                       inorder, index + 1, inEnd);
    return root;
}

6）通过中序遍历和后续遍历结果构造二叉树

后序遍历和前序遍历相反，根节点对应的值为postorder的最后一个元素。

TreeNode build(int[] inorder, int inStart, int inEnd,
               int[] postorder, int postStart, int postEnd) {

    if (inStart > inEnd) {
        return null;
    }
    // root 节点对应的值就是后序遍历数组的最后一个元素
    int rootVal = postorder[postEnd];
    // rootVal 在中序遍历数组中的索引
    int index = 0;
    for (int i = inStart; i <= inEnd; i++) {
        if (inorder[i] == rootVal) {
            index = i;
            break;
        }
    }
    // 左子树的节点个数
    int leftSize = index - inStart;
    TreeNode root = new TreeNode(rootVal);
    // 递归构造左右子树
    root.left = build(inorder, inStart, index - 1,
                        postorder, postStart, postStart + leftSize - 1);

    root.right = build(inorder, index + 1, inEnd,
                        postorder, postStart + leftSize, postEnd - 1);
    return root;
}

7）寻找重复的子树（中等）

如果你想知道以自己为根的子树是不是重复的，是否应该被加入结果列表中，你需要知道什么信息？

你需要知道以下两点：

1、以我为根的这棵二叉树（子树）长啥样？

2、以其他节点为根的子树都长啥样？

// 记录所有子树以及出现的次数
HashMap<String, Integer> memo = new HashMap<>();
// 记录重复的子树根节点
LinkedList<TreeNode> res = new LinkedList<>();

/* 主函数 */
List<TreeNode> findDuplicateSubtrees(TreeNode root) {
    traverse(root);
    return res;
}

/* 辅助函数 */
String traverse(TreeNode root) {
    if (root == null) {
        return "#";
    }

    String left = traverse(root.left);
    String right = traverse(root.right);

    String subTree = left + "," + right+ "," + root.val;

    int freq = memo.getOrDefault(subTree, 0);
    // 多次重复也只会被加入结果集一次
    if (freq == 1) {
        res.add(root);
    }
    // 给子树对应的出现次数加一
    memo.put(subTree, freq + 1);
    return subTree;
}

8）力扣第 297 题「二叉树的序列化与反序列化」

（1）前序遍历解法

序列化函数

String SEP = ",";
String NULL = "#";

/* 主函数，将二叉树序列化为字符串 */
String serialize(TreeNode root) {
    StringBuilder sb = new StringBuilder();
    serialize(root, sb);
    return sb.toString();
}

/* 辅助函数，将二叉树存入 StringBuilder */
void serialize(TreeNode root, StringBuilder sb) {
    if (root == null) {
        sb.append(NULL).append(SEP);
        return;
    }

    /****** 前序遍历位置 ******/
    sb.append(root.val).append(SEP);
    /***********************/

    serialize(root.left, sb);
    serialize(root.right, sb);
}

反序列化过程也是一样，先确定根节点 root，然后遵循前序遍历的规则，递归生成左右子树即可

/* 主函数，将字符串反序列化为二叉树结构 */
TreeNode deserialize(String data) {
    // 将字符串转化成列表
    LinkedList<String> nodes = new LinkedList<>();
    for (String s : data.split(SEP)) {
        nodes.addLast(s);
    }
    return deserialize(nodes);
}

/* 辅助函数，通过 nodes 列表构造二叉树 */
TreeNode deserialize(LinkedList<String> nodes) {
    if (nodes.isEmpty()) return null;

    /****** 前序遍历位置 ******/
    // 列表最左侧就是根节点
    String first = nodes.removeFirst();
    if (first.equals(NULL)) return null;
    TreeNode root = new TreeNode(Integer.parseInt(first));
    /***********************/

    root.left = deserialize(nodes);
    root.right = deserialize(nodes);

    return root;
}

（2）后顺遍历解法：

/* 主函数，将字符串反序列化为二叉树结构 */
TreeNode deserialize(String data) {
    LinkedList<String> nodes = new LinkedList<>();
    for (String s : data.split(SEP)) {
        nodes.addLast(s);
    }
    return deserialize(nodes);
}

/* 辅助函数，通过 nodes 列表构造二叉树 */
TreeNode deserialize(LinkedList<String> nodes) {
    if (nodes.isEmpty()) return null;
    // 从后往前取出元素
    String last = nodes.removeLast();
    if (last.equals(NULL)) return null;
    TreeNode root = new TreeNode(Integer.parseInt(last));
    // 限构造右子树，后构造左子树
    root.right = deserialize(nodes);
    root.left = deserialize(nodes);

    return root;
}

（3）中序遍历解法：

行不通。

（4）层级遍历解法：

首先，先写出层级遍历二叉树的代码框架：

void traverse(TreeNode root) {
    if (root == null) return;
    // 初始化队列，将 root 加入队列
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);

    while (!q.isEmpty()) {
        TreeNode cur = q.poll();

        /* 层级遍历代码位置 */
        System.out.println(root.val);
        /*****************/

        if (cur.left != null) {
            q.offer(cur.left);
        }

        if (cur.right != null) {
            q.offer(cur.right);
        }
    }
}

上述代码是标准的二叉树层级遍历框架，从上到下，从左到右打印每一层二叉树节点的值，可以看到，队列 q 中不会存在 null 指针。

不过我们在反序列化的过程中是需要记录空指针 null 的，所以可以把标准的层级遍历框架略作修改：

String SEP = ",";
String NULL = "#";

/* 将二叉树序列化为字符串 */
String serialize(TreeNode root) {
    if (root == null) return "";
    StringBuilder sb = new StringBuilder();
    // 初始化队列，将 root 加入队列
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);

    while (!q.isEmpty()) {
        TreeNode cur = q.poll();

        /* 层级遍历代码位置 */
        if (cur == null) {
            sb.append(NULL).append(SEP);
            continue;
        }
        sb.append(cur.val).append(SEP);
        /*****************/

        q.offer(cur.left);
        q.offer(cur.right);
    }

    return sb.toString();

可以看到，每一个非空节点都会对应两个子节点，那么反序列化的思路也是用队列进行层级遍历，同时用索引 i 记录对应子节点的位置：

/* 将字符串反序列化为二叉树结构 */
TreeNode deserialize(String data) {
    if (data.isEmpty()) return null;
    String[] nodes = data.split(SEP);
    // 第一个元素就是 root 的值
    TreeNode root = new TreeNode(Integer.parseInt(nodes[0]));

    // 队列 q 记录父节点，将 root 加入队列
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);

    for (int i = 1; i < nodes.length; ) {
        // 队列中存的都是父节点
        TreeNode parent = q.poll();
        // 父节点对应的左侧子节点的值
        String left = nodes[i++];
        if (!left.equals(NULL)) {
            parent.left = new TreeNode(Integer.parseInt(left));
            q.offer(parent.left);
        } else {
            parent.left = null;
        }
        // 父节点对应的右侧子节点的值
        String right = nodes[i++];
        if (!right.equals(NULL)) {
            parent.right = new TreeNode(Integer.parseInt(right));
            q.offer(parent.right);
        } else {
            parent.right = null;
        }
    }
    return root;
}