线型回归详解

线性回归

• 回归分析(regression analysis)用来建立方程模拟两

个或者多个变量之间如何关联

• 被预测的变量叫做：因变量(dependent variable), 

输出(output)

• 被用来进行预测的变量叫做： 自变量(independent 

variable), 输入(input)

• 一元线性回归包含一个自变量和一个因变量

• 以上两个变量的关系用一条直线来模拟

• 如果包含两个以上的自变量，则称作多元回归分析

(multiple regression)

 

ℎ𝜃 𝑥 = 𝜃₀ + 𝜃₁𝑥

方程对应的图像是一条直线，称作回归线。其中，

𝜃1为回归线的斜率， 𝜃0为回归线的截距。

 

 

 

 

求解方程

并不是我们随便作出一条回归线就行，我们需要作出一条使得真实值y都要紧密的在回归线边上，下面介绍几种方法看看怎么作出这个回归线。

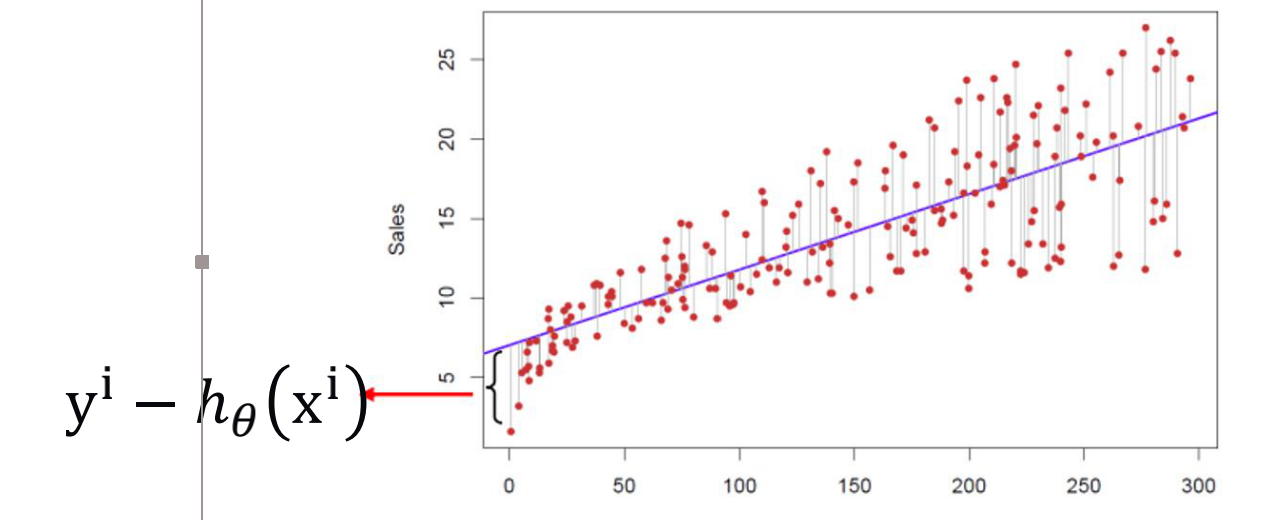
1、最小二乘法

最小二乘法的思想非常简单， 通过最小化误差的平方和寻找数据的最佳函数匹配，即求所有观察值的残差平方和的最小值。当然OLS回归是要在一定条件下的：

• Y的平均值能够准确地被由X组成的线性函数建模出来。
• 解释变量之间不存在线性关系（或强相关）。
• 解释变量和随机扰动项不存在线性关系。
• 假设随机扰动项是一个均值为0的正态分布。
• 假设随机扰动项的方差恒为 
• 假设随机扰动项是独立的。

 

剩下的问题我们是要求代价函数的最小值，这也是最小二乘的意思

 

 

 

 

目标 :求代价函数的最小值

 

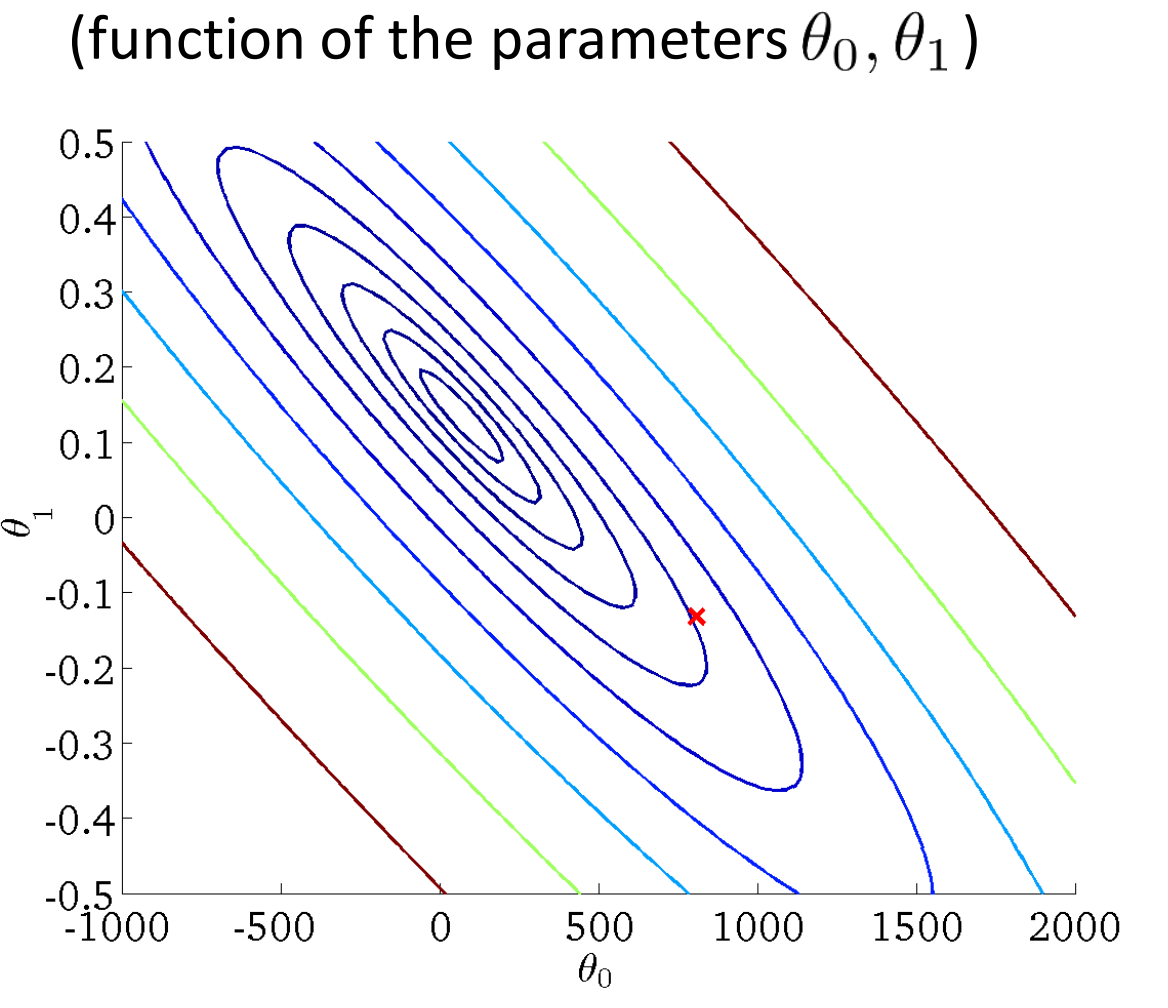
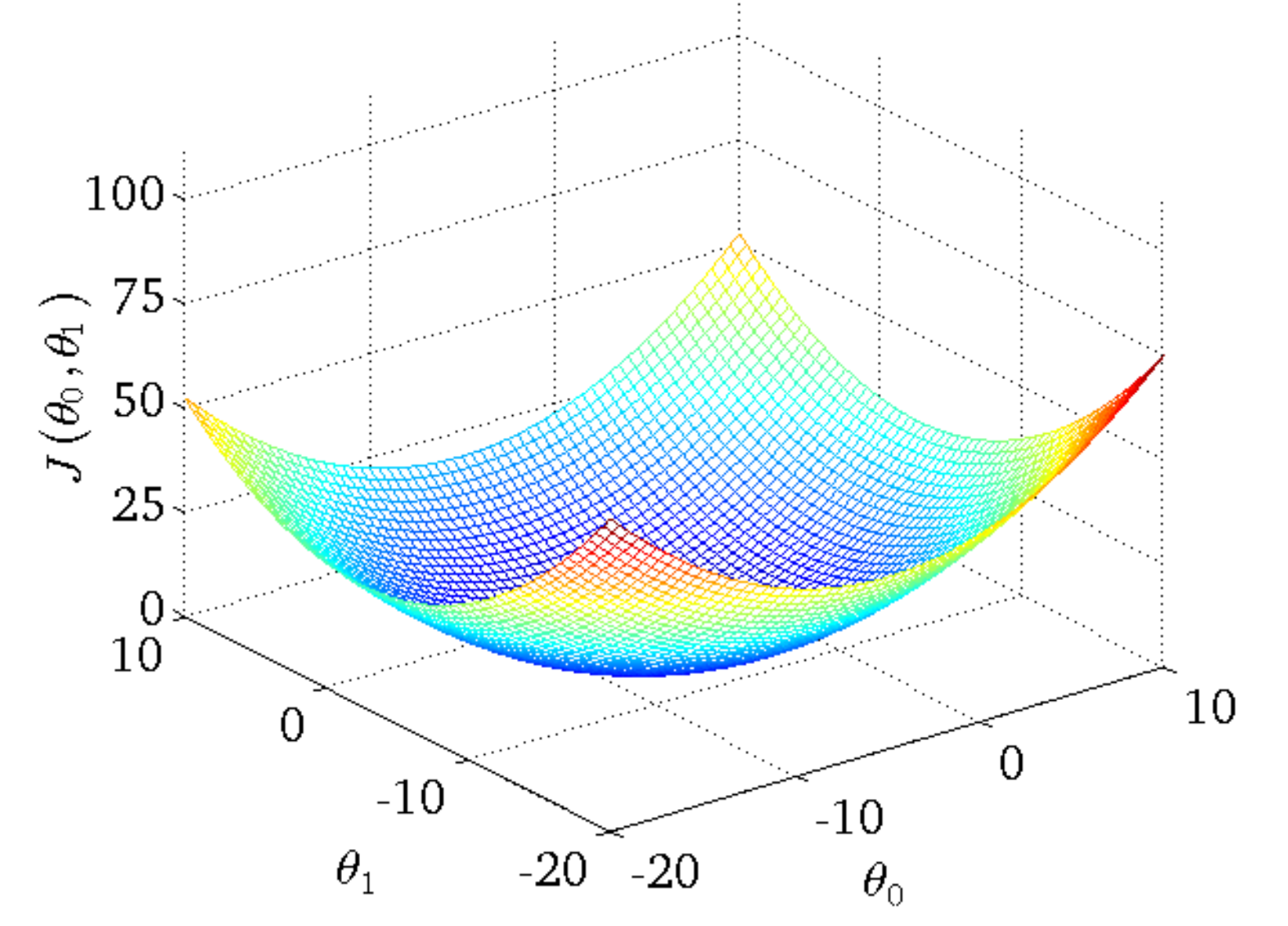
由图可知代价函数是关于θ₀和θ₁的二次方程，我们知道极值在导数为0的点

以下是我手动推导笔记（村里刚通网，不会电脑输公式)

 

 

 当然如果是多元线性回归思路也一样，就是计算复杂一点：

​ℎ𝜃 𝑥=θ₀​+θ₁​x₁+...+θ_p​x​_p

对每个θ求导

 

 

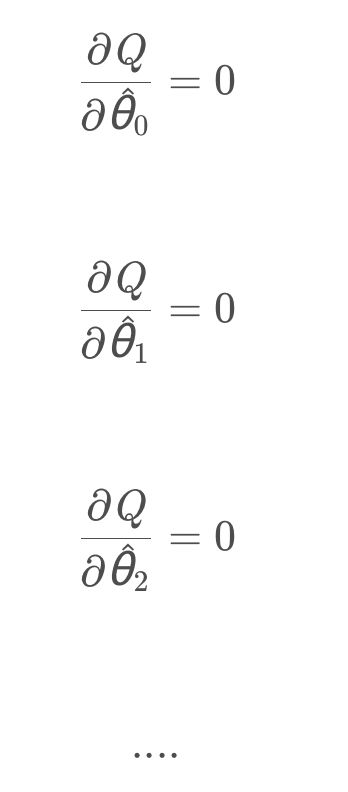
2、梯度下降法

我们注意到最小二乘法最后一步要求p个方程组，是非常大的计算量，其实计算起来很难，因此我们就有了一种新的计算方法，就是梯度下降法，梯度下降法可以看作是 更简单的一种 求最小二乘法最后一步解方程 的方法.

 

 

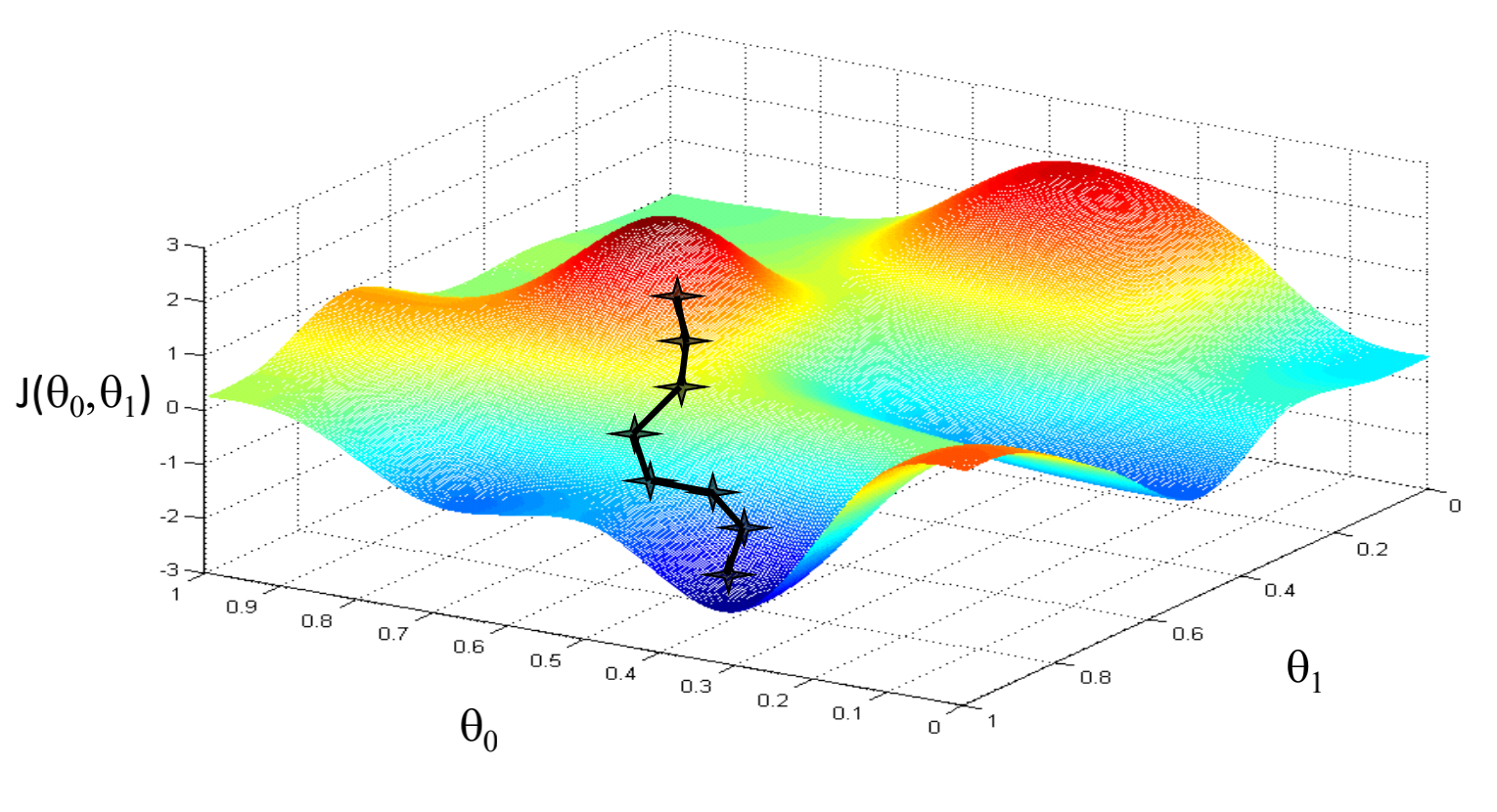
此图是梯度下降法工作原理。由图我们就像随机在一个坑洼地带，现在我们要通过不断尝试不同方向走路（改变θ₀和θ₁)以达到走到此地最低处（J(θ_0,θ₁)最小值）的目标。

那么现在问题来了，模仿让子弹飞里的台词：A:”第一步怎么走？第二步走到哪？“   B:”走到哪是第三步，我们先把第二步走好，第二步：步子迈多大？“（自娱自乐)。

梯度下降，不就是迭代θ₀和θ₁嘛，那么第一步来了：怎么走？是分别迭代θ₀和θ₁还是同时迭代θ₀和θ_1。答案是同时迭代θ₀和θ_1，有人会疑惑为什么不能一个个迭代？同时迭代能找到正确的梯度下降的方向，只迭代一个可能一开始方向就偏离了。其实这就好比咱们学习文理不能偏科一样，咱们高考也是偏科可能大学都考不上了。

 

 

 

我们经过努力迈出了人生正确的第一步，现在到第二步了：步子迈多大，这里的步子就是学习速率α。鲁迅说的好：步子迈大了容易扯*。那么我们的α多大就变得至关重要了，那么怎么选α的值呢，我能笃定的说我也不知道吗（手动捂脸）。大师们告诉我步子不能太大也不能太小。（我靠！这不是什么也没说，还无形中装了会逼），其实说白了就是凭着经验多尝试不同的值。这是吴大师的心决：

学习率不能太小，也不能太大，可以多尝试一些值

 

0.1,0.03,0.01,0.003,0.001,0.0003,0.0001…

 

现在第一步和第二步都走完了，到第三步就简单了，努力的方向和心决都有了那么剩下的就是一个字了”练！“。我们不断的重复一二步骤进行迭代，直至找到J(θ_0,θ₁)的最小值。

梯度下降的缺点是求得的值可能是局部最小值，并不是最小值。这不梯度下降法还蕴含着人生哲理"不要满足手中的98K，要的就是捡空投里的AWM"。

3、极大似然估计

极大似然估计个人理解： 当一件事情发生了，我们推算出它发生最有利的概率。比如抛硬币10次结果：6正，4反。那我们会想正面朝上的概率是多少，那还用想吗?!不就是6/10，那是小学解概率问题思路，现在我们用极大似然估计的思路来解。

令正面朝上的概率为p,那么反面朝上的概率就为1-p,那么出现6正4反的联合概率就是p⁶*(1-p)⁴。

L(x₁,x₂......x₁₀;p)=p⁶*(1-p)⁴

为了方便计算，把其转为对数似然函数，加个对数并不影响函数的方向。

ln(L(x₁,x₂......x₁₀;p))=ln(p⁶*(1-p)⁴⁾

ln(L(x₁,x₂......x₁₀;p))=6lnp+4ln(1-p)

用极大似然的思路，我们需要p值使得抛十次硬币6次朝上的概率最高。则我们对函数求导

ln'(L(x₁,x₂......x₁₀;p))=（6lnp+4ln(1-p))'=6/P+4/(P-1)=0

最后求得p=6/10

这就是极大似然估计的思路，当事件出现一个结果，我们找出出现这一结果的最高的概率。

 

好，现在我们怎么用这思路来求线型回归呢？

最小二乘的时候我们假设误差ε是均值为0的正态分布。我们用这一特性来搞点事情。  

转变成高斯分布概率函数：

 

 

 

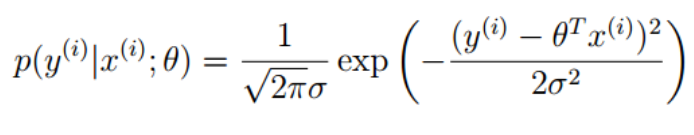
根据极大似然函数的思路，问题变成了我们知道x⁽ⁱ⁾,y⁽ⁱ⁾我们要找到θ的值使得高斯分布函数成立。

 

 

 

 

 

 

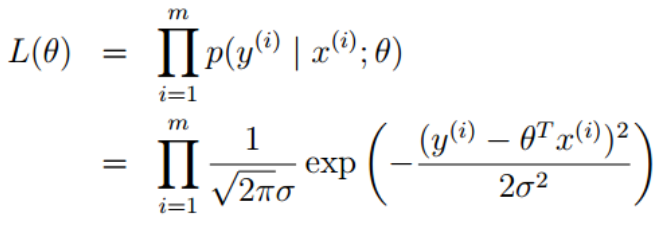
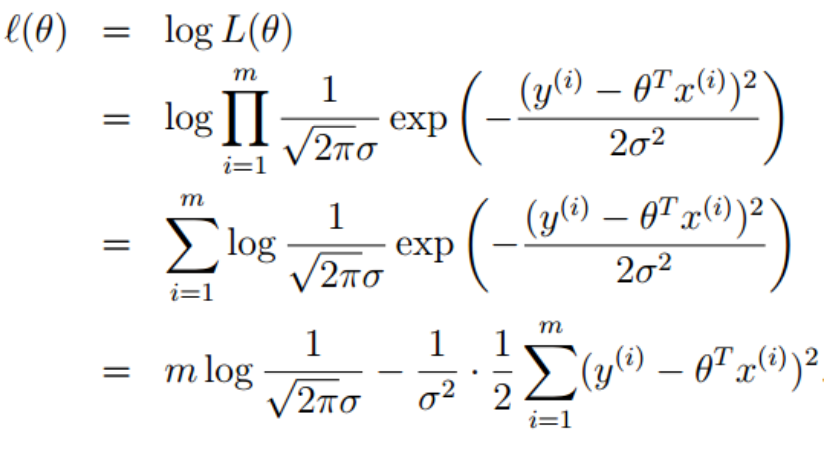
接下来求L(θ)的最大值，因为mlog1/（√2）*σ是常数，现在变为求J(θ)的最小值，问题又到了最小二乘问题上了。

 

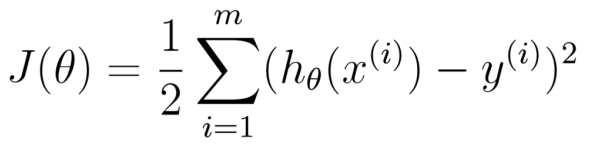
总结：对于线性回归而言最小二乘法是一本武林秘籍，极大似然估计是上半部心法，梯度下降是下半部心法。