快速幂算法（基于C++）

更高效地求解幂函数

　　说到幂函数，当然会联想到cmath头文件下的函数pow(底数，指数），但是如果自己写函数呢？

　　我想大多数人会跟我一样这么写：

int power(int a,int b)
{
    int ans=1;
    for(int i=1;i<=b;i++)
    {
        ans*=a;
    }
    return ans;
}

　　for循环暴力大法，显然这个方法没有错，但是时间复杂度不是很乐观，并且还存在溢出的问题。当求解问题的数据过多时，就会超时。

　　在解决溢出问题上，很多题目会要求必要的时候对运算结果合理地取模，当然取模也是有运算规则的。

　　下面就解决x^y%p这个问题，1 < x < 10^9 , 1 < y < 10 ^18, 1 < p < 10 ^9.

　　1.有一种递归的方法求解：看图

 

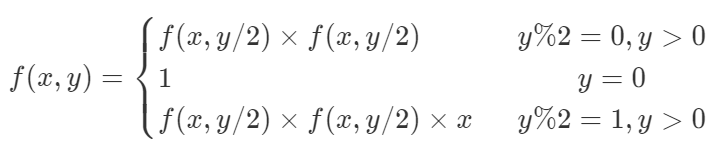
　　原理很简单，相当于分治的思想，先求一半，再平方，可以降低时间复杂度。

　　2.真正的快速幂，迭代思想

 1 long long power(long long x, long long y, long long p) {
 2     long long r = 1, base = x;
 3     while(y) {
 4         if(y % 2) r *= base;
 5         base *= base;
 6         y /= 2;
 7         base %= p;
 8         r %= p;
 9     }
10     return r;
11 }

　　　　快速幂拓展请看这里----->快速幂讲解<------里面附有斐波那契矩阵快速幂的代码

 

posted @ 2019-09-12 11:41  YE_Bob  阅读(1186)  评论(0)  编辑  收藏  举报