BUAA-OO-第三单元作业-JML之图论
OO第三单元JML规格之图论应用
一、JML语言说明
基础语法
1.requires子句定义该方法的前置条件(precondition), 方法执行前需要满足的条件;
2.副作用范围限定,assignable列出这个方法能够修改的类成员属性,\nothing是个关键词,表示这个方法不对任何成员属性进行修改,所以是一个pure方法。
3.ensures子句定义了后置条件,方法执行后需要满足这条语句的条件。
表达式
1.\forall表达式:全称量词修饰的表达式,表示对于给定范围内的元素,每个元素都满足相应的约束。
2.\exists表达式:存在量词修饰的表达式,表示对于给定范围内的元素,存在某个元素满足相应的约束。
3.\sum表达式:返回给定范围内的表达式的和。
4.\product表达式:返回给定范围内的表达式的连乘结果。
5.\max表达式:返回给定范围内的表达式的最大值。
6.\min表达式:返回给定范围内的表达式的最小值。
7.\num_of表达式:返回指定变量中满足相应条件的取值个数。
8.new JMLObjectSet {Integer i | s.contains(i) && 0 < i.intValue() } 表示构造一个JMLObjectSet对象
操作符
1.子类型关系操作符: E1<:E2,如果类型E1是类型E2的子类型(sub type),则该表达式的结果为真,否则为假。如果E1和E2是相同的类型,该表达式的结果也为真.
2. 等价关系操作符: b_expr1<==>b_expr2 或者 b_expr1<=!=>b_expr2 ,其中b_expr1和b_expr2都是布尔表达式,这两个表达式的意思是 b_expr1==b_expr2 或者 b_expr1!=b_expr2 。可以看出,
3. 推理操作符: b_expr1==>b_expr2 或者 b_expr2<==b_expr1 。对于表达式 b_expr1==>b_expr2 而言,当b_expr1==false ,或者 b_expr1==true 且 b_expr2==true 时,整个表达式的值为 true 。
4.变量引用操作符:除了可以直接引用Java代码或者JML规格中定义的变量外,JML还提供了几个概括性的关键词来引用相关的变量。\nothing指示一个空集;\everything指示一个全集.
5.关键词 also ,它的意思是除了正常功能规格外,还有一个异常功能规格.signals子句的结构为
Signals(***Exception e) b_expr.意思是当 b_expr 为 true 时,方法会抛出括号中给出的相应异常e。
类规格
### 数据抽象规格
- 数据抽象的内容、抽象操作描述
- 自定义数据结构,提高封装程度
- 数据抽象操作:
构造、更新、观察、生成
### 不变式与可变式
- 类规格应该保证对象操作有效
- 方法执行过程中有可能会修改成员变量(更新操作),即对象的不变式有可能不满足,则该过程必须为不可见状态;类规格强调任意可见状态下都要满足不变式。
##
- 继承往下的本质 扩充和扩展
- 继承往上的本质 隐藏和一般化
ps:继承具有严格的数据抽象层次约束,而接口可以自由跨越多个数据抽象层次
- 子类数据抽象=继承父类+自己新增的
- 子类数据规格=继承+扩展+新增
- 子类方法规格=继承+重写+新增
## 类型层次下规格关系
- 子类重写父类方法可以减弱规定的requre,或者加强ensure
## 规格设计的满足,类正确
- 基类
- 子类对象有效性
- 子类重写方法
## 集合元素的迭代访问
## 规格模式
- 约束类别:
相对约束、绝对约束
- 不变式在当前情况下式子成立条件不会改变、可变式
应用工具链
OpenJML
自动check JML规格文档并生成报告。
Junit自动测试类
二、JMLUnitNG测试类
Graph接口测试类

1 1 public void before() throws Exception { 2 2 int[] p1 = {1, 2, 3}; 3 3 int[] p2 = {1, 2, 3}; 4 4 int[] p3 = {1, 2, 3, 4, 5}; 5 5 path1 = new MyPath(p1); 6 6 path2 = new MyPath(p2); 7 7 path3 = new MyPath(p3); 8 8 graph.addPath(path1); 9 9 graph.addPath(path2); 10 10 graph.addPath(path3); 11 11 } 12 12 13 13 @After 14 14 public void after() throws Exception { 15 15 } 16 16 17 17 @Test 18 18 public void testAddPath() { 19 19 Assert.assertEquals(1, graph.addPath(path1), 1); 20 20 Assert.assertEquals(1, graph.addPath(path3), 1); 21 21 } 22 22 23 23 @Test 24 24 public void testContainsNode() { 25 25 Assert.assertEquals(1, graph.addPath(path1), 1); 26 26 Assert.assertEquals(1, graph.addPath(path2), 1); 27 27 Assert.assertTrue(path3.containsNode(1)); 28 28 Assert.assertTrue(graph.containsNode(5)); 29 29 Assert.assertEquals(1, graph.addPath(path3), 1); 30 30 Assert.assertTrue(graph.containsNode(5)); 31 31 } 32 32 33 33 @Test 34 34 public void testRemovePath() { 35 35 Assert.assertEquals(1, graph.addPath(path1), 1); 36 36 Assert.assertEquals(1, graph.addPath(path3), 1); 37 37 Assert.assertEquals(1, graph.addPath(path1), 1); 38 38 Assert.assertEquals(1, graph.addPath(path3), 1); 39 39 }
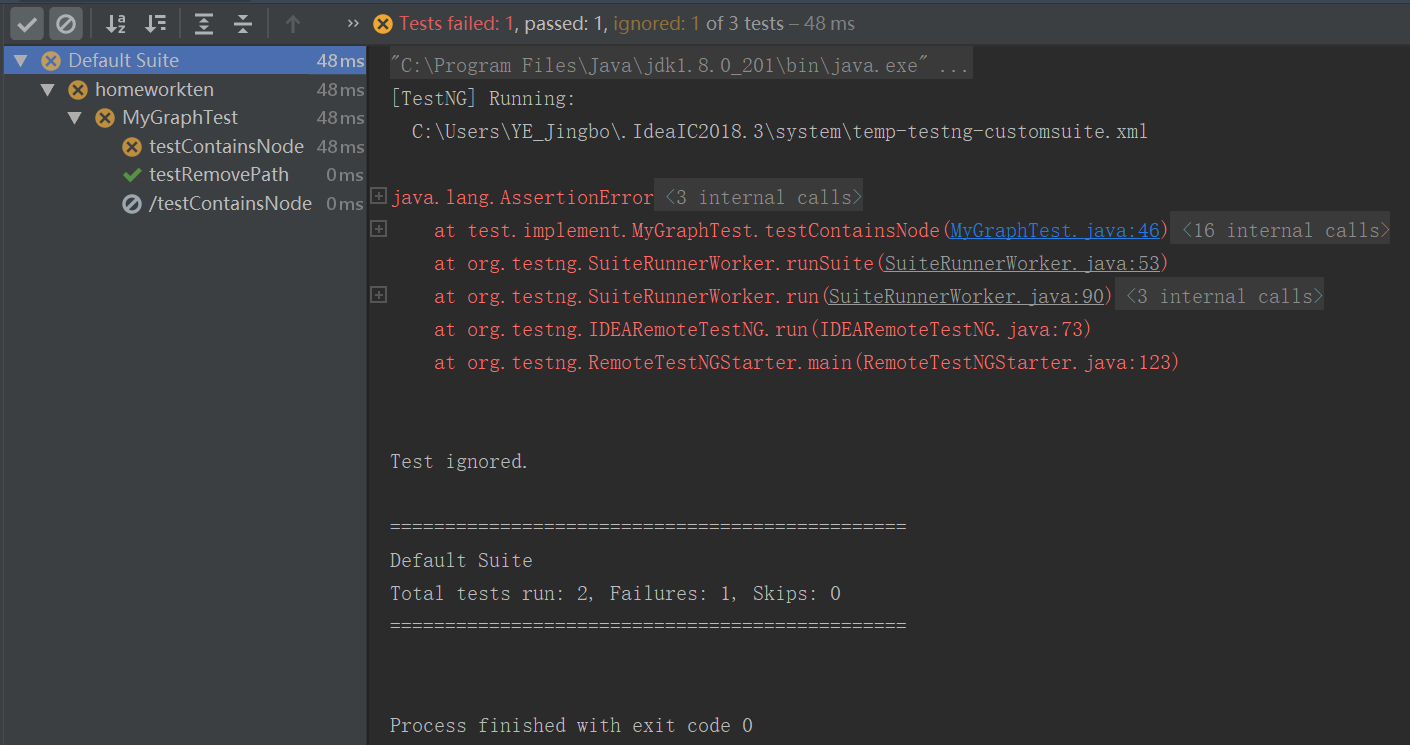
测试三个方法,ContainsNode, addPath, RomovePath.
利用断言添加预期结果和实际运行结果的判断,以及真假表达式。
报告结果
三、架构设计
第一次:
设计思考
1.本次作业我们知道,通过继承Path、PathContainer两个官方提供的接口,来实现自己的MyPath、MyPathContainer容器;本题有添加、删除、查询路径,查询节点,查询路径id,求不同节点数等操作。对这些功能我们看起是很熟悉的,也知道不涉及高级数据结构,通过阅读JML文档也知道,只需实现即可,后续再考虑时间复杂度的优化。首先读懂JML规格文档,可以按照JML文档所表达的意思构建代码,可以保证正确性,但不一定保证是最优的(往往这种情况只是为了简明解释该方法的功能,而忽略其性能,性能是程序员需要考虑的)。
2.路径结构想到的是利用Arraylist容器进行存储节点数组,和路径数组,然后方便遍历和查找,有jdk已有的方法,只需调用即可。后来发现,Arraylist容器底层的操作,遍历查找都是通过for循环逐个查找的,效率显然是底下的。因此会考虑到HashMap或者Hashset,LinkedHashset,我选择了后两个。
架构层次
基础层
- MyPath
- MyPathContainer实现官方接口的类
数据结构层
- 对容器进行添加、删除Path,计算容器内不同节点数;
- 对每个Path进行查找节点,计算不同节点数
缓存计算层
- 对不同节点数求解可以缓存,每次增加或删除Path时重新计算
应用层
- PathContainer
第二次:
设计思考
1.继承Path、Graph两个官方提供的接口,通过设计实现自己的Path、Graph容器,来满足接口对应的规格。
2.Graph容器继承了上次作业的PathContainer接口,为其拓展了一些本次作业新增的功能,实际上,MyPath类和MyPathContainer类可以保持不变,然后让MyGraph实现即可。
3.增加一些指令和功能:容器中是否存在某一条边、两个结点是否连通、两个结点之间的最短路径。此题需要构建图的数据结构,然后进行相应功能的计算。
架构层次
基础层
- MyPath
- MyPathContainer实现官方接口的类
- MyGraph类
数据结构层
- Struct图结构类:用于存储图,判断节点连通性,求解最短路
缓存计算层
- 对不同节点数求解、节点连通性、最短路可以缓存,每次增加或删除Path时重新计算
图建模层
- 通过Map<idPath, path>映射关系,以及节点nodeId map <nodeId, nodeNum>映射关系建立图结构。
应用层
- MyGraph中的各种功能
第三次:
设计思考
1.继承Path、RailwaySystem两个官方提供的接口,通过设计实现自己的Path、RailwaySystem容器,来满足接口对应的规格。
2.同Path类可以复用之前的实现,只需增加RailwaySystem新增的接口功能即可
3.新增指令,整个图中的连通块数量、两个结点之间的最低票价、两个结点之间的最少换乘次数、两个结点之间的最少不满意度简单来说,对于同一个图,需要有四种功能,四种求解。一般情况下,是将四种功能单独开来,构建四个类建图管理。
架构层次
基础层
- MyPath
- MyPathContainer实现官方接口的类
- MyGraph类
- MyRailwaySystem
数据结构层
- ShortestPath:最短路求解类
- ConnectB:联通块求解类
- LeastTrans:最少换乘类
- LeastPrice :最低票价类
- LeastUnp:最低不满意度类
缓存计算层
同第二次作业,每种功能计算都可以利用数组进行缓存,只有当add,remove指令时更新
图建模层
四个类,四种图建模,同一种图映射关系。
应用层
- MyRailwaySystem
四、总结分析
第一次Path、PathContainer类实现
任务
- 阅读JML规格编写相应的类和方法从而实现接口。
- 指令功能:添加路径、删除路径、根据路径id删除路径、查询路径id、根据路径id获得路径、获得容器内总路径数、根据路径id获得其大小、根据径id获取其不同的结点个数、根据结点序列判断容器是否包含路径、根据路径id判断容器是否包含路径、容器内不同结点个数、输入指令格式:DISTINCT_NODE_COUNT、根据字典序比较两个路径的大小关系、路径中是否包含某个结点
值得注意的是:程序的最大运行cpu时间为10s。因此不只是简单考虑用迭代器进行遍历查找,应该考虑更高效的查找方法。
本题思路
本次作业高级算法应该说是没有的,低级算法也说不上有,只是一些简单的路径操作,另外,本单元知识和图论数据结构类似,相当于重新用了一边图论,自己建立数据结构,再进行遍历算法。
本题有添加,删除,查询路径,查询节点,查询路径id,求不同节点数等操作。
1.首先读懂JML规格文档,可以按照JML文档所表达的意思构建代码,可以保证正确性,但不一定保证是最优的(往往这种情况只是为了简明解释该方法的功能,而忽略其性能,性能是程序员需要考虑的)。
2.路径结构想到的是利用Arraylist容器进行存储节点数组,和路径数组,然后方便遍历和查找,有jdk已有的方法,只需调用即可。后来发现,Arraylist容器底层的操作,遍历查找都是通过for循环逐个查找的,效率显然是底下的。
因此会考虑到HashMap或者Hashset,LinkedHashset,我选择了后两个。
Hashset和LinkedHashset能够去除容器中的重复元素,构成集合,唯一区别就是,LinkedHashset保持了元素连接关系,也就是保持了顺序。在去重这一应用上,此题的复杂度降低了不少,在实际生活中,对大量数据的处理也很有用。
查找某一节点是否存在于路径中,也即该路径是否包含这个节点,我也运用Hashset去重,大大降低了复杂度,另外HashSet的contains方法是利用key-value来映射查找的,因此比for循环更快。
1 public boolean containsNode(int node) { 2 HashSet<Integer> arr = new HashSet<>(nodes); 3 if (arr.contains(node)) { 4 return true; 5 } 6 return false; 7 }
求解路径不同节点数,也是类似方法,创建一个Hashset容器,往容器里添加每条路径的节点数组,自动去重,最后只需返回该容器的大小即可。
1 private void distinctNodeCount() { 2 HashSet<Integer> arr = new HashSet<>(); 3 for (Path it : paList) { 4 HashSet<Integer> nodes = new HashSet<>(((MyPath) it).getMyPath()); 5 arr.addAll(nodes); 6 } 7 count = arr.size(); 8 }
对于本题和后两道题,还有一个可以考虑优化的点,就是不需要每次查找重新计算不同节点数,而是每次改变路径的时候,增加或者删除,才去计算,所以可以利用变量进行存储当前计算结果,访问的时候直接返回即可。
3.Main类和方法
1 public class Main { 2 public static void main(String[] args) throws Exception { 3 AppRunner runner = AppRunner.newInstance( 4 MyPath.class, MyPathContainer.class); 5 runner.run(args); 6 } 7 }
4.对于Path类要求实现的还有两个东西,一个是迭代器,一个是比较器。
迭代器直接利用
1 return nodes.iterator(); 2 3 比较器自己写了一个类似于字符串比较的代码 4 5 public int compareTo(Path o) { 6 int len = nodes.size(); 7 if (nodes.size() > o.size()) { 8 len = o.size(); 9 } 10 for (int i = 0; i < len; i++) { 11 if (this.getNode(i) != o.getNode(i)) { 12 return Integer.compare(this.getNode(i), o.getNode(i)); 13 } 14 } 15 return Integer.compare(this.size(), o.size()); // equal 16 }
Debug
本次作业比较简单,没有找到大家的bug,基本上都是时间复杂度没有仔细考虑而超时,我自己也是一个例子,第一次写根本没有优化。之后才考虑优化的。
但是,在Hashset处理的时候也有可能会出现一点问题,HashSet是不保证元素顺序的,它每次都会根据hash值来进行排序,所以会造成影响,因此用LinkedHashset。
还需要注意的是增加和删除路径,对于和其他路径节点重复的节点不应该删除。
度量分析
类图
除去官方接口自己写的只有三个类:Main,MyPath,MyPathContainer
MyPath实现Path接口,MyPathContainer实现Container接口:




代码行数

复杂度
此次代码长度不长,另外有了JML规格文档,对代码规范要求程度上升,其实大家写的都类似于规格文档所规定的。从这次作业开始,我逐渐模仿规格文档和官方接口里的范例写方法功能注释,类注释,接口注释等信息。
第二次Graph类实现
任务
- 继承Path、Graph两个官方提供的接口,通过设计实现自己的Path、Graph容器,来满足接口对应的规格。Graph容器继承了上次作业的PathContainer接口,为其拓展了一些本次作业新增的功能,实际上,MyPath类和MyPathContainer类可以保持不变,然后让MyGraph实现即可。
- 增加一些指令:容器中是否存在某一条边、两个结点是否连通、两个结点之间的最短路径。
值得注意的是:任意时刻容器中所有的节点数不超过250,而不是一次测试中所有节点数不超过250。
解题思路
我复用了第一次作业已优化且调试正确度高的代码,此次只增加了Graph接口里新增的方法功能,如新增指令描述。
显然,这次是一个图的数据结构,有求解两个节点之间的最短路径,判断两个节点是否连通以及判断是否存在一条边。
考虑到图结构,当然需要建图,已知任何时可已存在的图节点数不超过250,所以我们是否可以开一个250*250的graph[][]数组呢?继续看,节点id符合整型,意味着节点可以是很大(123456789)或者很小(-12345678)的数,此时再单纯地用二维数组是不够的。我们需要考虑对节点的映射,将存入的节点映射到[0,249]这个区间内,因为时刻保证不会超出这个范围。(当然稍微大一点255也可以毕竟250不好听)。
说到映射,这个肯定是运用HashMap来进行映射,本次作业也多次用到HashMap来查找,从而减少时间复杂度。
图结构的存储及映射关系如下:
/* <idPath, path> */ private static HashMap<Integer, Path> map = new HashMap<>();
节点映射关系以及一些定义如下:
1 /* nodeId map <nodeId, nodeNum>*/ 2 private static HashMap<Integer, Integer> nodeMap = new HashMap<>(); 3 4 private static int idPath = 0; // unique path id 5 private static int count = 0; // store all distinct nodes 6 private static int nodeNum = 0; // nodeNum of map nodeId
idPath是路径id,count用来存储当前时刻不同节点数,nodeNum就是用来计算更新当前容器中所有的节点,方便映射。
3.最短路求解我直接采用floyd算法,对整个图进行搜索,然后顺便标记连通矩阵(即可达性矩阵),只要dis[][]非最大,即存在边。
4.这是这次新增的为了方便计算图结构的类,计算最短路和判断连通性一起实现的:
1 private StructGraph struct = new StructGraph(); 2 3 /** 4 * 图结构类 5 * 说明: 6 * 计算连通性,用可达性矩阵存储 7 * 计算最短路径,Floyd算法 8 * PS:这两个操作可以一起执行,都是在写入指令后重新计算 9 */ 10 11 相关定义: 12 13 /* map nodeId to graph */ 14 private boolean[][] graph = new boolean[MAX_Node][MAX_Node]; 15 private int[][] dis = new int[MAX_Node][MAX_Node]; // shortest dis 16 /* connected */ 17 private boolean[][] connected = new boolean[MAX_Node][MAX_Node]; 18 19 每次通过节点映射关系取得数组下标: 20 21 int nodeU = nodeMap.get(nodes.get(i)); 22 int nodeV = nodeMap.get(nodes.get(i + 1));
Debug
任意时刻容器中所有的节点数不超过250,而不是一次测试中所有节点数不超过250。
我因为理解错这句话,导致我强侧只有15分,然后de完bug快速AC了。一不小心没注意到,酿成大祸。后来花了一天时间写了评测器、对拍器,然后没有用上。除了这个bug其他问题就是求最短路的问题,我直接使用floyd算法bug不多。当然时间复杂度稍微高一点。
度量分析
类图
此次代码增加了管理图结构的类StructGraph,其余的符合接口要求。



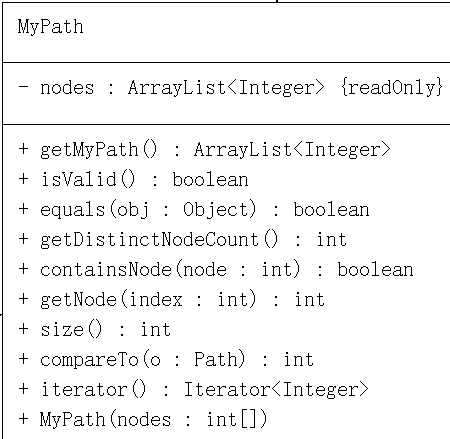

代码行数

复杂度
在图结构上增加了功能,且运用了数据结构的算法,此次作业的代码量总体还可以,算法都学过能较快写出来,主要是转化思路的问题。
第三次Path、RailwaySystem类实现
任务
- 继承Path、RailwaySystem两个官方提供的接口,通过设计实现自己的Path、RailwaySystem容器,来满足接口对应的规格。
- 同样Path类可以复用之前的实现,只需增加RailwaySystem新增的接口功能即可(正如助教所说的OOP思想)。
- 新增指令:整个图中的连通块数量、两个结点之间的最低票价、两个结点之间的最少换乘次数、两个结点之间的最少不满意度。
解题思路
1.形如第二次作业,新增四个类方便管理这四种功能,单独求解。

/* Railway class */ // blockCount private static int blockCount; // block count private ConnectB block = new ConnectB(); // connected block private static boolean firstAdd = true; // addPath weather first // transCount private LeastTrans trans = new LeastTrans(); // UnpleasentCount private LeastUnp unPleasent = new LeastUnp(); // Price private LeastPrice price = new LeastPrice();
2.最容易实现的功能是求解连通块数,利用并查集(外加压缩路径算法)轻松判断;然后就是换乘求解,边权设置为0,对每个path连通更新边权(此情况不用更新),最后每条联通的边权值都+1,求最短即可,后面的类似。

1 /** 2 * 最低不满意度 3 * F(u) = (int)(u % 5 + 5) % 5, H(u) = pow(4, F(u)) 4 * 边E(u,v)的不满意度 UE = max(H(u), H(v)) 5 * 每进行一次换乘会产生 UnP = 32 点不满意度 6 * 对于一条路径,UPath = sum(UE) + y * Unp, y为换乘次数 7 * 存储边权值,权值即为该边的不满意度 UE + 32,将该path构造为完全图 8 * 用Floyd算法求带权图最短路 9 */ 10 11 /** 12 * 最低票价 13 * x为经过的边数,y为换乘次数,票价PPath = x + 2 * y 14 * 存储边权值,权值为该边的票价,即 1 + 2,将该path构造为完全图 15 * 用Floyd算法求带权图最短路 16 */ 17 18 /** 19 * 连通块数 20 * 并查集,addPath可以增加,但每次remove需要重算 afresh 21 * 添加 unio(x, y), (x, y) <==> (nodeMap.get(x), nodeMap.get(y)) 22 * 考虑路径压缩find 23 */ 24 25 /** 26 * 基本图结构类 27 * 说明: 28 * 计算连通性,用可达性矩阵存储 29 * 计算最短路径,Floyd算法 30 * PS:这两个操作可以一起执行,都是在remove指令后重新计算 31 */ 32 33 /** 34 * 最少换乘 35 * 存储每个node所在路线号,并存储边权,权值初始化为INFINITY 36 * 对于每条path内,边权值初始化为1,即不需要换乘,将该path构造为完全图 37 * Floyd算法求最短路,(weight求和 - 1)为最少换乘次数 38 */
3.并查集路径压缩算法:
判断该节点是否是根节点,如果不是,则找到它的根节点,然后依次将它以及它的祖先节点(但非根节点的节点)都标记为根节点的儿子节点,最终的结果也就是一个根节点下其余的都是兄弟节点,而没有父子关系了。
1 protected int pressedFind(int x) { 2 int parent = father.get(x); 3 while (parent != father.get(parent)) { 4 parent = father.get(parent); 5 } 6 int pre; 7 int cur = x; 8 while (cur != father.get(cur)) { 9 pre = father.get(cur); 10 father.put(cur, parent); 11 cur = pre; 12 } 13 return parent; 14 }
Debug
显然很多Bug,中测倒数第二个最后关头都没找出来,所以没进互测,然后时间复杂度特别高,对于强侧的数据,简直爆炸了。
当然bug修复还在进行中。改进了求最短路的算法,修复了超时的问题。对于最低票价和不满意度是最容易存在Bug的,而对于并查集求解基本没有问题。最低票价我采用上文的思路,仍会出现问题,有这几种:单条路径存在环路需要更新权值;每条路径都需要求最短路;新增路径与原有路径存在相同节点也需要更新。
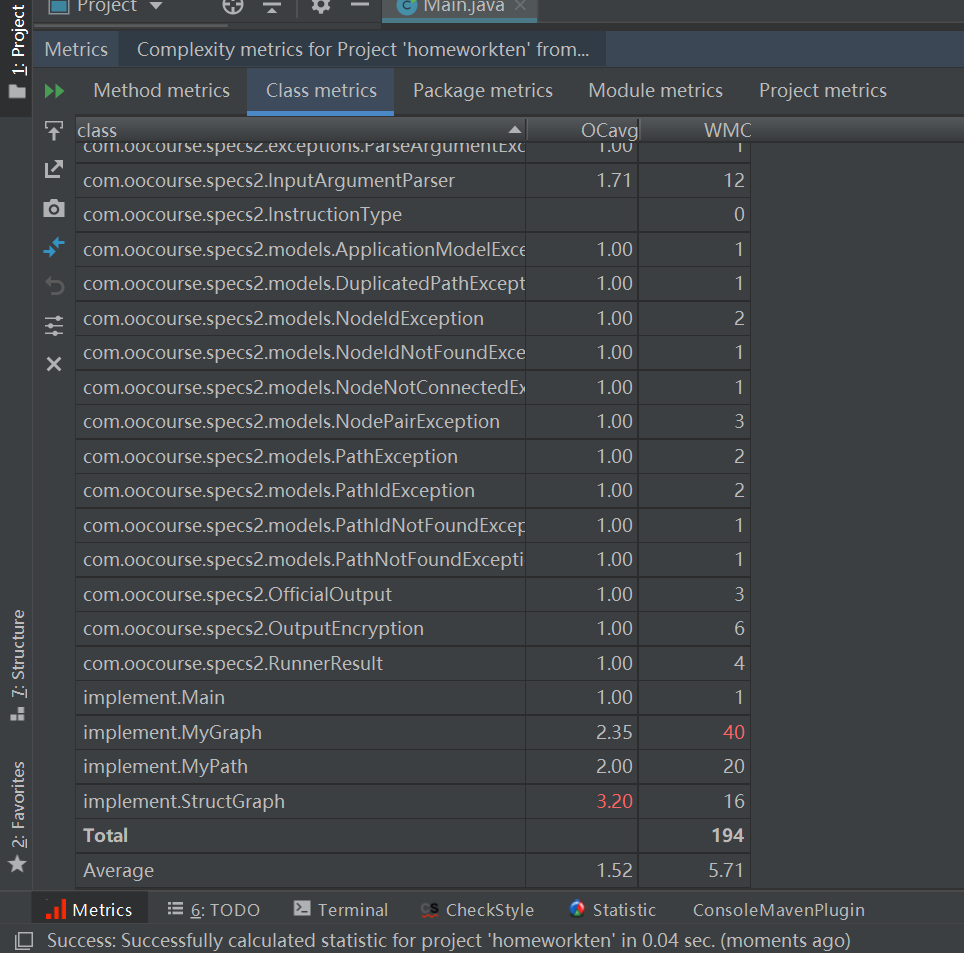
度量分析
类图
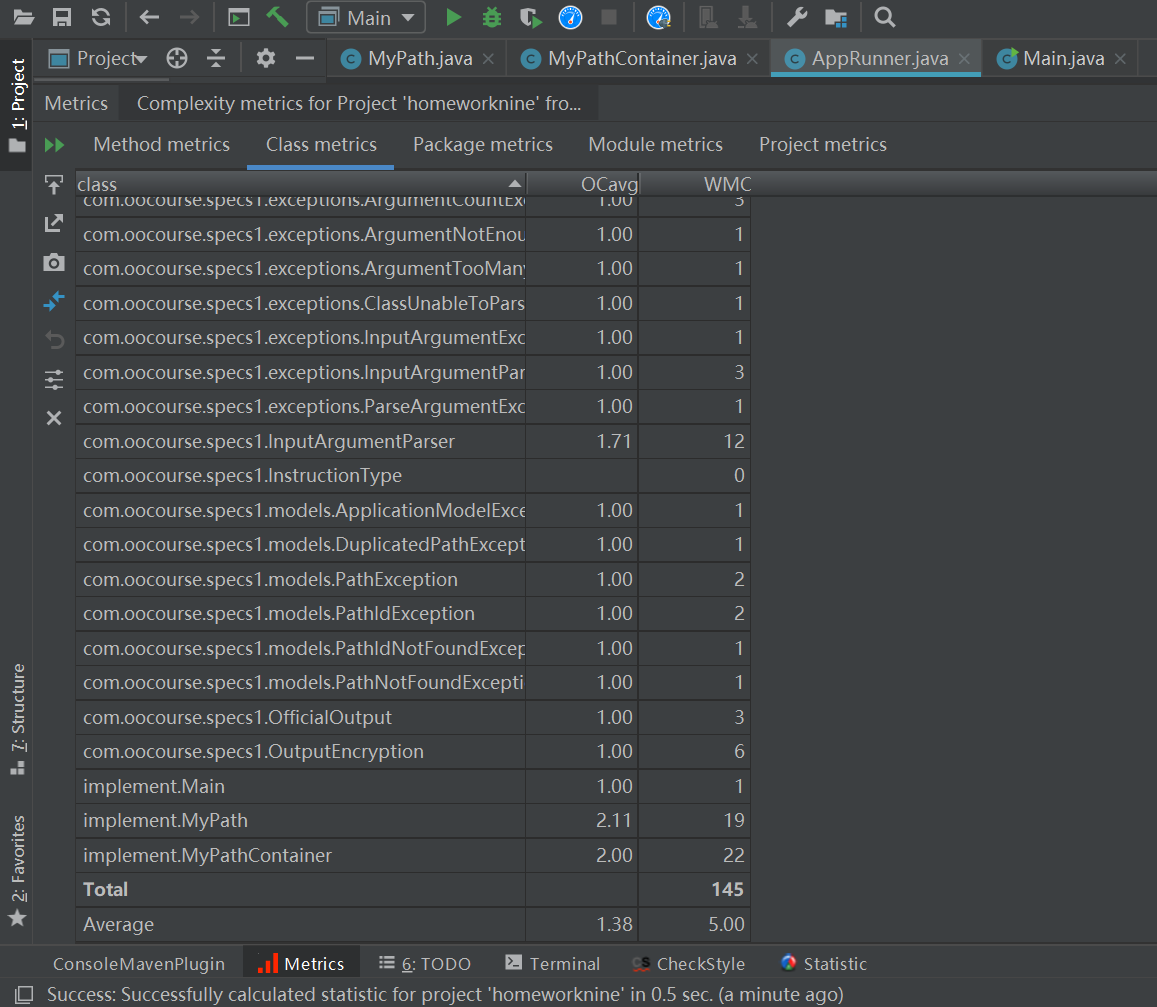
本次作业相当于新构建了四个图,每个图实现一个功能,所以代码量显然增加了许多(bug也是)。








代码行数

复杂度
首先看了讨论区大佬的一些发言,有许多没有看明白,能让我接受的还是针对每种情况,对边权的存储也不同,不拆点,但是造成的后果就是时间复杂度高,每条路径都需要求最短路。后来我只能改进求最短路算法,我对于其他拆点求解不感冒。