2024 Nov

Question 1. [ARCY 2021] E. Planning Railroad Discontinuation

给定 \(l\) 张 \(n\) 个点 \(m\) 条边的图 \(G_i(0\leq i < l)\)，其中图 \(G_i\) 中连接 \(u,v\) 两个点的边的边权为 \(w_{u,v} + b_i\)。

在所有图中钦定 \(r\) 个点 \(s_1,s_2,\cdots, s_r\)，作为特殊点，其中点 \(G_i\) 的点 \(s_i\) 的特殊边仅连接 \(G_{(i-1)\bmod l}\) 与 \(G_{(i+1)\bmod l}\) 的点 \(s_i\)，边权分别为 \(a_{(i-1)\bmod l}\) 与 \(a_i\)。

记 \(G\) 是所有 \(G_i\) 与所有特殊边的并，求 \(G\) 的最小生成树。

\(n\leq 10^4, m,l \leq 10^5, w_{u,v},a_i,b_i\leq 10^9\)

---

nb 题。

首先让我们考虑 Kruskal 算法的过程：选出边权最小的边然后连上这条边。在本题中，由于 \(G\) 的点与边的数量巨大，无法直接执行 Kruskal，考察 \(G\) 的特殊性质。

让我们先将求 \(G_i\) 内部的生成树时，有效的边进行分类：连上这条边时，两个连通块均包含特殊点的，至少有一个不包含特殊点的。前者的所有边的边权按照从小到大的顺序记录下来，记为 \(S\)。

将所有 \(G_i\) 内部的生成树全部建好，然后考虑所有特殊边带来的贡献：减掉内部的边、连上特殊边。

还是根据 Kruskal，我们接下来要连通 \(G_i\)，那么肯定是根据 \(a_i\) 的升序考察，连出 \(l-1\) 组特殊边即可。

假设当前 \(a_i\) 两端的连通块的最小生成树已经求出，当前需要合并这两个连通块，那么肯定是 \(b_i\) 较大的那一边断开部分边，满足 \(w_{u,v} + b_j \ge a_i\)，这一点可以通过对 \(S\) 进行后缀和与二分求出数量与总和。

合并之后，两个连通块的 \(b_j\) 值肯定会取较小的那一个，不断重复直至所有连通块全部合并成功。

Question 2. 「JOI 2021 Final」集体照

给定一个长度为 \(n\) 的全排列 \(H\)，你需要通过执行下述操作尽可能少的次数，使得 \(\forall 1\leq i < n, H_i < H_{i+1} + 2\)：

• 选择一个正整数 \(i\) 满足 \(1\leq i < n\)，然后交换 \(H_i, H_{i+1}\)。

\(n\leq 5000\)

---

首先，\(H_i < H_{i+1} + 2\) 等价于 \(H_{i+1}\ge H_i - 1\)，也就是说，满足条件的排列 \(P\) 可以用如下方式生成：

• 设 \(P_0 = \{1,2,\cdots,n\}\)。
• 选择若干个互不相交的区间 \([l_i,r_i]\)，然后在 \(P_0\) 中翻转这些区间。

接下来就比较容易了，设 \(f_i\) 表示考虑到值为 \(i\)，当前需要交换的对数的数量的最小值。

为了转移，我们设 \(g_{l,r}\) 表示值在 \([l,r]\) 范围内的元素在原 \(H\) 中的逆序对数量，\(h_{l,r}\) 表示原 \(H\) 中满足较小值在 \([1,l)\) 范围，较大值在 \([l,r)\) 内的逆序对数量，则：

\[f_i = \underset{j < i}{\min} f_j + h_{j+1,i} + \min(g_{j+1,i}, \dbinom{i-j}{2} - g_{j+1,i}) \]

暴力计算 \(g,h\) 的时间复杂度为 \(\mathcal{O}(n^4)\) 外加一个小于 \(1\) 的常数。

发现以 \(l,r\) 分别为横轴与纵轴，那么原 \(H\) 中一对逆序对 \(H_i,H_j\) 所贡献的分别是一个子矩形，而且在 \([1,n]\times [1,n]\) 的最右端，二维差分优化即可。

时间复杂度为 \(\mathcal{O}(n^2)\)，可以通过。

Question 3.「JOI 2023 Final」现代机器

Bitaro 生日这天收到了一个 JOI 机作为生日礼物。JOI 机由一个球，\(N\) 条光带和 \(M\) 个按钮组成。光带从 \(1\) 到 \(N\) 编号。当 Bitaro 打开开关时，光带 \(i\ (1\le i\le N)\) 会发出颜色 \(C_i\) 的光（蓝光 (\(\texttt{B}\)) 或红光 (\(\texttt{R}\))）。按钮从 \(1\) 到 \(M\) 编号。如果 Bitaro 按下按钮 \(j\ (1\le j\le M)\)，将发生如下事情。

1. 把球放置在光带 \(A_j\) 上。

2. 光带 \(A_j\) 变成红色（不管它原来是什么颜色）。

3. 进行如下操作，直到球被移除。

   令 \(p\) 为球目前所在的光带编号。

   • 如果光带 \(p\) 是蓝色，
     光带 \(p\) 变为红色。在此之后，如果 \(p=1\)，这个球就被移除。否则，球移向光带 \(p-1\)。
   • 如果光带 \(p\) 是红色，
     光带 \(p\) 变为蓝色。在此之后，如果 \(p=N\)，这个球就被移除。否则，球移向光带 \(p+1\)。

Bitaro 对 JOI 机十分感兴趣。他计划进行 \(Q\) 次实验。在第 \(k\ (1\le k\le Q)\) 次实验中，在 Bitaro 开启电源后，他将按 \(L_k,L_k+1,\ldots R_k\) 的顺序按下这些开关。在 Bitaro 按下一个开关后，他将等到球被移除后再按下下一个开关。

给定 JOI 机和实验的情况，写一个程序计算对于每个实验，当实验结束后红色的光带有多少。

注：每次实验之间互相独立。

对于 \(100\%\) 的数据：\(3\leq N\leq 120,000, 1\leq M,Q\leq 120,000\)。

---

子任务 1（累计 3 分）

这个问题的直接模拟，时间复杂度为 \(\mathcal{O}(QN^2M)\)。

子任务 2（累计 15 分）

先默认已经将球所在的光带变为红色，发动惊人注意力，可以注意到如下结论：

• 如果球的起始位置是 \(x\)，且球最终从左边滚落，那么从左到右的 \(x\) 个蓝色光带会变为红色。
• 如果球的起始位置是 \(x\)，且球最终从右边滚落，那么从右到左的 \(N + 1 -x\) 个红色光带会变为蓝色。

证明一下（以左边滚落为例）：

• 首先，因为它能从左边滚落，所以（向左的步数）-（向右的步数）为 \(x\)。

• 其次，考虑光带的变化为这个差所带来的影响：

  • 没有变色的，则经过的次数为偶数，所以在该光带上（向左的步数）-（向右的步数）的值为 \(0\)。
  • 从红色变为蓝色的，经过次数为奇数，最后一步向右，所以在该光带上（向左的步数）-（向右的步数）的值为 \(-1\)。
  • 从蓝色变为红色的，经过次数为奇数，最后一步向左，所以在该光带上（向左的步数）-（向右的步数）的值为 \(1\)。

• 且由于，\(x\) 从左边掉落，所以不会有红色变为蓝色的光带，故从蓝色变为红色的数量为 \(x\)，且一定是最左边的，反之就一定不合法。

类似可以证明右边掉落的情况。

根据这个方法，我们每个球最终所带来的影响很好求解：

• 如果蓝色的光带的数量 \(\ge x\)，那么球会从左边掉落。
• 反之，球会从右边掉落。

时间复杂度为 \(\mathcal{O}(QNM)\)。

子任务 3（累计 25 分）

我们可以再发现两个重要事实：

1. 前缀红色光带的范围与后缀蓝色光带的范围缓慢增加。
2. 当存在一个点，其左边全部为红色光带、右边全部为蓝色光带的时候，那么接下来的任意时刻，也一定总是存在一个点满足前述条件。

当我们知道这两个事实之后。

根据第一个事实，我们尝试预处理出下面两个参数：

• \(L_i\)，表示从左往右第 \(i\) 个光带为蓝色，要使其变为红色，它初始要在从左往右第几个光带上。
• \(R_i\)，表示从右往左第 \(i\) 个光带为红色，要使其变为蓝色，它初始要在从右往左第几个光带上。

根据第二个事实，再度往下探究，可以注意到如下结论：

• 如果球被放置在第 \(x\) 个光带上，且变色之后有 \(y\) 个光带为红色，则接下来会有 \((x+y)\bmod (N+1)\) 个光带是红色。

证明参考子任务 2 的那个结论。

那么接下来就比较简单了，首先暴力模拟至第二个事实满足的时刻：

• 注意设立 \(c\) 表示是否初始位置是一个蓝色光带，如果是。
  • 其前缀红色光带的拓展范围加上 \(1\)
  • 或其后缀蓝色光带的拓展范围减去 \(1\)。

随后枚举计算之后的状况即可。

时间复杂度为 \(\mathcal{O}(QM)\)。

子任务 4（累计 36 分）

如果根据子任务 3，那么它相当于已经做完了所谓【暴力模拟至第二个事实满足的时刻】的过程。

该子任务等价于模拟以下代码：

cnt=10;
n=10;
for(int i=l;i<=r;i++)
{
    if(cnt<a[i])
        cnt=(cnt+a[i]+1)%(n+1);
    else
        cnt=(cnt+a[i])%(n+1);
}

考虑在线段树上维护这个东西：

设 \(X_{u,i}\) 表示在 \(u\) 节点所对的子树下，\(i\) 为初始值得到的结果。

设 \(l,r\) 分别为左右儿子，那么 \(X_{u,i} = X_{r,X_{l,i}}\)，于是可以合并。

时间复杂度为 \(\mathcal{O}((N+1)M + Q\log_2 M)\)，即线段树的预处理与询问。

子任务 5（累计 62 分）

如果根据子任务 3，那么它相当于已经做完了所谓【暴力模拟至第二个事实满足的时刻】的过程。

相较于子任务 4，其实模拟的代码并没有很大改变，无非就是改了 \(cnt\)，并且 \(N\) 的范围大了许多而已。

不可能还是存储 \(X_{u,i}\)，此时空间复杂度为 \(\mathcal{O}(NM)\)。

那么怎么做呢？考虑如下一个优化：

• 将累加值相同的值进行压缩，并存储它们所对应的区间。

这个东西比较经典，时间复杂度为 \(\mathcal{O}((M+Q)\log_2^2M)\)。

实际写起来抽象程度还是相当之高，这里附 pushup 的实现：

inline void pushup(int id)
{
    auto &Set=seg[id<<1|1].res;
    for(auto [inL,inR,outL,outR]: seg[id<<1].res)
    {
        int p=lower_bound(Set.begin(),Set.end(),(Interval){outL+1,M-1,0,0})-Set.begin()-1;
        int q=lower_bound(Set.begin(),Set.end(),(Interval){outR+1,M-1,0,0})-Set.begin()-1;
        if(outL>outR)
            q+=Set.size();
        for(int j=p;j<=q;j++)
        {
            int rl=j%Set.size();
            int dL=outL,dR=outR;
            if(outL>outR)
            {
                if(j>=Set.size())
                   dL=0;
                else
                    dR=M-1;
            }
            dL=max(dL,Set[rl].inL);
            dR=min(dR,Set[rl].inR);
            int bef=(inL-outL+M)%M;
            int aft=(Set[rl].outL-Set[rl].inL+M)%M;
            seg[id].res.push_back(
                {(bef+dL)%M,(bef+dR)%M,(aft+dL)%M,(aft+dR)%M}
            );
        }
    }
}

子任务 6（累计 79 分）

在子任务 3 中我们提出了两个重要事实，并为事实 2 提出了结论。

在子任务 4,5 中我们为事实 2 提出了线段树的快速解决方法，时间复杂度为 \(\mathcal{O}((M+Q)\log_2^2 M)\)。

本子任务中，\(A_i\) 距边缘不超过 \(20\)，尝试优化事实 1。

如果条件【左边 \(20\) 个全部是红色，右边 \(20\) 个全部是蓝色】成立的话：

• 设 \(A_i\) 距左右两端的距离分别为 \(d_L,d_R\)，那么：
  • 如果 \(d_L\leq 20\)，增加 \(d_L\) 个红色光带。
  • 否则，增加 \(d_R - 1\) 个红色光带。

如果如此，二分出红蓝色的碰撞时间即可。

条件不成立的话，则假设左边 \(a\) 个全是红色，右边 \(b\) 个全是蓝色。

• 依旧设 \(A_i\) 距左右两端的距离分别为 \(d_L,d_R\)，那么：
  • 如果 \(d_L\leq a\)，增加 \(d_L\) 个红色光带。
  • 如果 \(d_R\leq b\)，增加 \(d_R - 1\) 个蓝色光带。
  • 其余情况，Hmm...

其余情况，似乎并不好处理，但是思考一下，这样的操作最多不超过 \(40\) 个，这 \(40\) 个操作暴力执行即可。

为了实现其余的二分相关，求出前若干个操作对红色光带的增量，以及区间内红色光带的数量是必要的。

设 \(K= 40\)，时间复杂度为 \(\mathcal{O}(QK\log_2 M + (M+Q)\log_2^2M)\)。

本子任务不做实现。

子任务 7（累计 100 分）

单看最上面的所述，【其余情况】发生次数的量级如何？看起来很像是每一个都有可能，即 \(\mathcal{O}(M)\) 个，实际上并不是。

• 假设【其余情况】发生了，且球的初始摆放位置是 \(x\)，假设左边 \(a\) 个全是红色，右边 \(b\) 个全是蓝色。
  • 如果球从左边下落，那么左边会有至少 \(2a\) 个变为红色。
  • 如果球从右边下落，那么右边会有至少 \(2b\) 个变为蓝色。

所以这样的操作最多只会执行 \(\mathcal{O}(\log_2 N)\) 次，但是我们需要快速找出这些操作。

这些满足 \(a+1\leq A_i\leq N-b\) 的最小的 \(i\)。

如果采用线段树上归并的方式求解，时间复杂度相当之高，也就是 \(\mathcal{O}(Q\log_2^3M + (M+Q)\log_2^2M)\)，Hmm...

换个做法吧，设 \(f(x)\) 表示不超过 \(x\) 的最大的 \(2^k\) 的值，那么考虑 \(f(a)+1\leq A_i\leq N-f(b)\) 最小的 \(i\)。

预处理 \(H_{p,q,k}\) 表示 \(f(a) = 2^p, f(b) = 2^q\) 时 \(k\) 后的一个最小的合法的 \(i\) 的值。

时空复杂度为 \(\mathcal{O}(N\log_2^2N)\)，查询单次是 \(\mathcal{O}(1)\) 的，正确性呢？

• 如果这种【其余情况】发生了，\(f(a),f(b)\) 发生改变的一方，至少 \(\times 2\)，所以不会有影响。

在前一个子任务中，我们求出前若干个操作对红色光带的增量，以及区间内红色光带的数量是必要的。

本子任务中，我们需要对 \(2\) 的每个幂次都跑出对应的增量。

注意由于可能初始时 \(a=0\) 或者 \(b=0\)，所以 \(2\) 的幂次处理时最好也保留一个 \(0\)。

当然再注意，如果第 \(N\) 个光带初始为蓝色，那么将球摆放在第 \(N\) 个光带上开始没有任何影响。

可能你需要小心一些奇奇怪怪的边界情况，比如最后在线段树上查询时 \(l > r\) 什么的。

于是最终的复杂度为 \(\mathcal{O}(Q\log_2N(\log_2N+\log_2M)+(M+Q)\log_2^2M)\)。

Question 4. [Northern Eurasia Finals 2022] B. BinCoin

有一棵 \(n\) 个结点的二叉树，保证非叶子结点有 \(2\) 个儿子，按照如下方式生成树的遍历序：

• 从根节点开始：
• 如果当前结点没有儿子，将自己的编号追加到遍历序的末尾。
• 否则：
  • 先随机选择一个儿子，进入该儿子的子树。
  • 遍历完一棵子树后，将自己的编号追加到遍历序的末尾。
  • 进入另一个儿子的子树。

注意，各节点选择儿子是独立事件。

按照上述方式生成 \(k\) 个遍历序，给定这些遍历序，还原二叉树的结构：你需要告知每个结点的父亲结点。

\(n\leq 999, 50\leq k\leq 100\)

---

二叉树结构还原有一个比较有效的方法：找到根，划分两个子树，递归处理。

我们如何找到根结点？其左右两边产生的结点集合只有 \(2\) 种——左子树与右子树，如果不是根，那么极大概率不止两个，根据题解：为两个的概率不超过 \(\dfrac{1}{250}\)。

判定集合相等比较容易考虑到 Hash，随机权异或、质数幂次与取模等都可以。

找到根节点后，递归处理，错误率不超过 \(1 - (1 - \dfrac{1}{250} ) ^ {500} \approx 4\times 10^{-13}\)。

由于两个子树在各个遍历序中的左右可能不同，你可以将 Hash 值小的当作左子树，大的当作右子树，递归的时候把当前遍历序中的结点一并当参数递归，可能方便一些。

Question 5. [Northern Eurasia Finals 2022] D. Dominoes

给定一张 \(n\times m\) 的网格图，每个网格要么可以被覆盖，要么不可以被覆盖，铃音将要用 \(1\times 2\) 的多米诺骨牌覆盖所有可以被覆盖的网格，且不覆盖任何不可以被覆盖的网格。

保证初始网格图可以被完美的覆盖。

彼时香穗非常 Naughty，她会选择两个可以被覆盖的网格，将它们的状态置为不可以被覆盖，她希望这一步操作之后的网格图不可以被完美的覆盖。

求总方案数，但是方案数可能非常大，你只需要将其与 \(10^6\) 取 \(\min\) 即可。

\(n,m\leq 1000\)

---

比较容易发现相当于原二分图具有完美匹配，接下来你需要扔掉两个点与与之相连的所有边，让操作后的二分图不具有完美匹配。

如果两个点来自同一个点集，那么显然操作后的二分图不具有完美匹配，先算出这样的方案数 \(B\)。

若 \(B\ge 10^6\)，程序输出 \(10^6\) 后即可停止，反之，设二分图的点集为 \(V\)，边集为 \(E\)，则 \(|V|\leq 2000\)，由于点的度数不超过 \(4\)，则 \(|E|\leq 4000\)，可以跑一发匈牙利算法。

如果删去的一对点属于完美匹配，那么显然可以删去，每次删除两个点之后跑一下复杂度为 \(\mathcal{O}(|V|^2|E|)\)，比较劣。

假设我们需要 check 一对点 \((u,v)\)，如果 \(u\) 到 \(v\) 有交错路径，那么我们可以沿着这条路依次调整每一对匹配，最终使得合法，反之无法调整，那么一定不合法。

那么我们可以预处理每一个左部点沿交错路的可达位置，随后枚举并 \(\mathcal{O}(1)\) 判断合法性，时间复杂度为 \(\mathcal{O}(|V||E|+|V|^2)\)。

DP Tips

当考虑从前往后 DP，而状态中涉及到后缀的信息的，可以将全串作为后缀，每次向后转移的时候，将后缀的信息进行更改（一般是减少某个数值），如果有不确定的，初始化时酌情考虑对每一种情况附特定的初始值。

例：[3rd-Ucup, Stage 0] I. Not Another Constructive!

Programming with puzzles

1. 数字华容道 完全版

2. 滚珠魔方 I

Question 6. [3rd-Ucup, Stage 0] L. Square of Triangles

给定 \(4\) 个三角形三边长的平方，求这四个三角形能不能完美的拼成一个正方形。

多测。

\(T\leq 20, 1\leq a,b,c\leq 10^7\)

---

极致的大分讨体验！

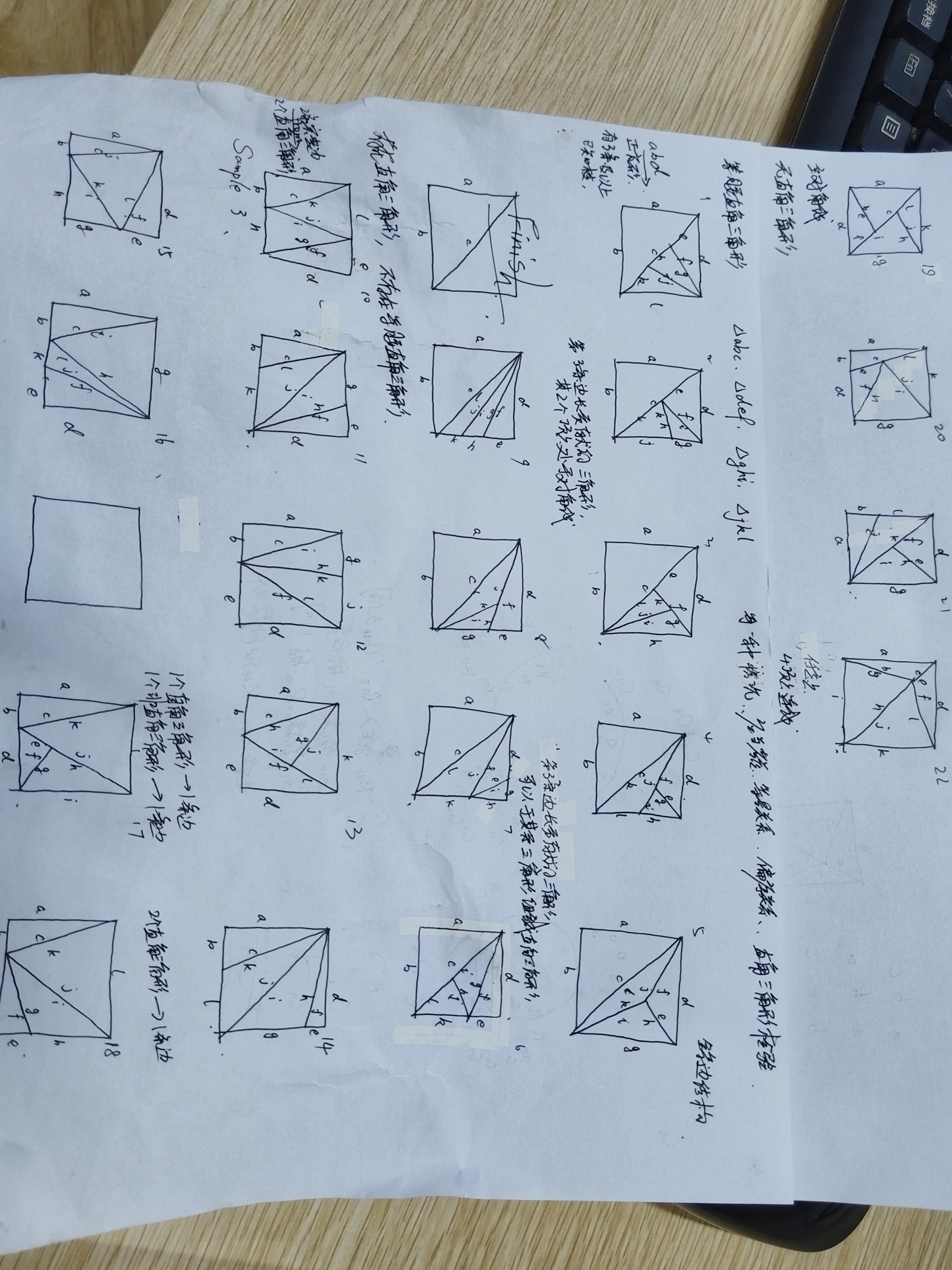
总共 \(22\) 种情况。

\(12\) 条边，我们钦定 \(abc,def,ghi,jkl\) 分属四个三角形，用 \(24\times 6^4\) 的次数枚举对应关系即可。

至于分讨，直接看图即可，注意不要弄错边，需要注意的是：除去等量关系以外，偏序关系也不能丢掉，面积可以帮助去除许多不合法情况。

Question 7. [3rd-Ucup, Stage 0] C. Comparator

假定一个程序 \(f\) 接受两个范围为 \([0,2^k)\) 的参数 \(x,y\)，这个程序 \(f\) 有 \(n\) 个 if 语句，按照顺序判定每一个 if，如果条件成立即刻返回，返回值为 \(0\) 或 \(1\)，条件是取 \(x\) 的从低往高第 \(a\) 位与 \(y\) 的从低往高第 \(b\) 位作为 \(x',y'\) 代入某个逻辑表达式计算是否为真。

判定 \(f\) 能否构建偏序关系，对下面三项分别计数：

• 不满足自反性的元素 \(x\) 的数量，即 \(f(x,x) = 0\) 不成立。
• 不满足反对称性的元素对 \((x,y)\) 的数量，即【若 \(f(x,y) = 1\)，则 \(f(y,x) = 0\)】不成立。
• 不满足传递性的元素三元组 \((x,y,z)\) 的数量，即【若 \(f(x,y) = f(y,z) = 1\)，则 \(f(x,z) = 1\)】不成立。

\(n\leq 10^5, \sum |expr|\leq 10^6, k\leq 10\)

---

每个表达式可以构建为 \((a,x,b,y)\) 有可能有特定的返回值 \(r\)，每一个 \((a,x,b,y)\) 相当于只有第一次出现有用，总共有 \(4k^2\) 个这样的四元组，每个四元组枚举 \(2^{2k}\) 填充 \(f\) 的结果表即可。

假设你已经知道了 \(f(x,y)\) 的所有值，那么第一项与第二项可以枚举计算，时间复杂度为 \(\mathcal{O}(2^k)\) 与 \(\mathcal{O}(2^{2k})\)。

第三项考虑对所有 \(f(x,z) = 0\) 求出有多少个 \(y\) 使得 \(f(x,y) = f(y,z) = 1\)，可以 bitset 优化。

时间复杂度为 \(\mathcal{O}(\sum |expr| + k^22^{2k} + \frac{2^{3k}}{\omega})\)。

Question 8. [3rd-Ucup, Stage 0] M. Training, Round. 2

Hinata 打算进行一场试炼，这场试炼总共有 \(n\) 关，Hinata 有初始攻击力 \(A\) 与防御力 \(D\)，对于每一关：

• 可以选择跳过这一关，之后这一关不能再被选择。
• 若满足攻击力 \(A\in [al_i,ar_i]\) 且防御力 \(D\in [dl_i, dr_i]\)，则可以选择通过这一关，之后必须选择攻击力与防御力其中之一，让其加 \(1\)。

求最多通过多少个关卡。

\(n\leq 5000, A,D,ar_i,dr_i\leq 10^9\)

---

一个二元组 \((\Delta a,\Delta d)\) 只要达到，那么之后就一定可以达到（不断跳过）即可，问题就是维护二元组 \((\Delta a,\Delta d)\)。

对于每个 \(\Delta a\)，维护已经更新到的 \(\Delta d\) 的集合与尝试更新的 \(\Delta d\) 的集合，每次就是在一个矩形内将尝试更新的更新掉。

如果 \((i,j)\) 被更新了，则将 \((i,j+1),(i+1,j)\) 加入尝试更新的集合。

时间复杂度为 \(\mathcal{O}(n^2\log_2 n)\)。

Question 9. 【MX-S6-T4】「KDOI-11」彩灯晚会

给定一张连通的 DAG，共计 \(n\) 个点，\(M\) 组边，每一组边方向为 \(u_i\to v_i\)，共 \(w_i\) 条，不同组的边方向不同。

为每个点标记一个 \(1\sim k\) 的点权，设点权为 \(i\) 的点共组成了 \(c_i\) 条长度为 \(l\) 个点的链，求所有标记方法的 \(\overset{k}{\underset{i=1}{\sum}} c_i^2\) 的总和。

答案对 \(P = 998244353\) 取余。

\(n\leq 300, M\leq \frac{n(n-1)}{2}, k < P, l\leq 20\)

---

根据组合意义，贡献式表示有序地选择两条长度为 \(l\) 个点的同色链的方案数。

设这两条链交于 \(v\) 个点，则方案的贡献系数为 \(k^{n - 2l + v + 1}\)。

恰好 \(v\) 个点的贡献较难维护，考虑二项式反演转为【钦定】若干个点为交点。

接下来考虑 DP，按照拓扑序做就可以搞掉链所带来的一些奇奇怪怪的限制，设 \(dp_{u,p,q,r}\) 表示当前钦定最后一个交点为 \(u\)，两条链的长度分别为 \(p,q\)，目前钦定了 \(r\) 个交点。

那么转移显然是 \(dp_{u,p,q,r} \times f_{u,v,d_1}\times f_{u,v,d_2} \to dp_{v,p+d_1,q+d_2,r+1}\)，系数基于 \(f_{u,v,l}\) 表示 \(u\to v\) 且长度为 \(l\) 的链的数量。

初始值基于 \(ed_{u,l}\) 表示到点 \(u\) 结束的长度为 \(l\) 的链的数量，统计答案时基于 \(st_{u,l}\) 表示到从 \(u\) 开始的长度为 \(l\) 的链的数量。

记得计算钦定没有交点的方案数，为所有 \(f_{u,v,l}\) 的总和的平方。

显然 \(f\) 是好做的，而 \(g\) 发现没有同时跟 \(d_1,d_2\) 有关的，考虑 \(dp_{u,p,q,r} \times f_{u,v,d_1}\to h_{v,p+d_1,q,r}, h_{v,p+d_1,q,r}\times f_{u,v,d_2} \to dp_{v,p+d_1,q+d_2,r+1}\)。

此时的时间复杂度为 \(\mathcal{O}(n^2l^4 + n^3l)\)，不够优秀。

考虑一下我们计算答案的时候，我们真的基于了每个 \(c\) 的方案数吗，我们只需要计算每个 \(k^c\) 的系数，直接把这个 \(k^c\) 转移的时候一并计算就可以了。

由于我们有二项式反演这个东西，不能直接 \(\times k\)，考虑化一下式子：

\[\begin{aligned} g'_i &= \overset{l}{\underset{j=i}{\sum}} (-1)^{j-i} \dbinom{j}{i} g_j \\ S &= \overset{l}{\underset{i=0}{\sum}} k^{n-2l+i+1}g'_i \\ &= \overset{l}{\underset{i=0}{\sum}} k^{n-2l+i+1} \overset{l}{\underset{j=i}{\sum}} (-1)^{j-i} \dbinom{j}{i} g_j \\ &= k^{n-2l+1} \overset{l}{\underset{i=0}{\sum}} \overset{l}{\underset{j=i}{\sum}} (-1)^{j-i} \dbinom{j}{i} g_j k^i \\ &= k^{n-2l+1} \overset{l}{\underset{i=0}{\sum}} \overset{l}{\underset{j=i}{\sum}} k^j (-1)^{j-i} \dbinom{j}{i} g_j (k^{-1})^{j-i} \\ &= k^{n-2l+1} \overset{l}{\underset{j=0}{\sum}} k^jg_j \overset{j}{\underset{i=0}{\sum}} \dbinom{j}{i} (-\dfrac{1}{k})^{j-i} \\ &= k^{n-2l+1} \overset{l}{\underset{j=0}{\sum}} k^jg_j \overset{j}{\underset{i=0}{\sum}} \dbinom{j}{i} (-\dfrac{1}{k})^{j-i}1^i \\ &= k^{n-2l+1} \overset{l}{\underset{j=0}{\sum}} k^jg_j (1-\dfrac{1}{k})^j \\ &= k^{n-2l+1} \overset{l}{\underset{j=0}{\sum}} g_j (k-1)^j \\ \end{aligned} \]

可得：转移系数为 \((k-1)\)，于是每多钦定一个交点，即 \(h\times f\to dp\) 转移时额外带一个 \(k-1\) 的系数，且初始钦定第一个交点的时候也需要乘一个 \((k-1)\)。

此时的时间复杂度为 \(\mathcal{O}(n^2l^3 + n^3l)\)，足以，抛弃一些加上 \(0\) 的转移可以优化常数。

Question 10. [3rd-Ucup, Stage 0] B. Champernowne Substring

生成模式串 \(P = 123456789101112\cdots\)，接下来给出文本串 \(T\)，含有通配符 ?，你需要计算文本串 \(T\) 在哪个位置第一次匹配上模式串的连续子串。

多测。

\(Case\leq 10, |T|\leq 25\)

---

首先，如果匹配位置的数字很小，那么会有一些 Corner，先暴力特判掉这种情况，实测达到 \(15,000\) 即可，下设所有出现过的数字都至少有 \(5\) 位。

如果匹配的位置跨过了 \(10^x\)，那么也有一些 Corner，也暴力特判掉，下设所有出现过的数字位数相同。

如果没有进位，则考虑 ?????1?????2?????3?????4...?????9 这样的模式，枚举判定是否可以匹配即可，这里没有什么 Corner，注意首位不为 \(0\)。

否则如果有进位，考虑进位将多少个 \(9\) 进位成了 \(0\)，枚举进位数，考虑 ?????995?????996...?????999?????000?????001...?????003?????004 这样的模式，枚举判定是否可以匹配，注意匹配的最前面的 \(9\) 在前面一位受到进位要加 \(1\)。

所有没有任何限制的 ? 能填 \(0\) 就填 \(0\)，如果在最高位则填 \(1\)，位置是好求的，考虑模式串出现的第一个数即可，最高进位的 \(9\) 的前一位如果是数的最高位，可能要填 \(1,2\) 而不能填 \(0,1\)。

具体还是有一些细节。

Question 11. [3rd-Ucup, Stage 0] K. Shadow Line

设 \(x = w\) 是墙，点光源 \(L\) 初始位于 \((0,0)\)，平面上有 \(n\) 条竖直线段 \((x,[yl,yr])\)，点光源发出的光被线段阻挡会在墙上造成一段阴影，将点光源沿 \(x\) 轴负半轴移动，求墙上只有恰好一段阴影时点光源的可能位置区间的长度总和。

如果有一段向无穷远处的区间，则答案为 \(-1\)。

\(n\leq 3000, w\leq 10^6, 0 < x < w\)，所有 \(y\) 坐标互不相同。

---

不妨考虑每一条线段所造成的阴影区间，点光源 \(L\) 向线段两端点连射线交墙于 \(P,Q\) 两点，则 \([y_P,y_Q]\) 构成阴影。

只有恰好一段阴影可以等价于它们的并是一段。

因为只有恰好一段阴影 \(\Longleftrightarrow\) 只有恰好两个点是阴影与照亮区的分界点，接下来考察每个区间阴影与照亮区的分界点的数量。

从下往上，遇到一个下端点的投影点则 \(+1\)，上端点的投影点则 \(-1\)，则可以从下往上做前缀和，遇到为 \(0\) 的则为分界点，注意先更新上端点后判分界再更新下端点。

不妨考察两条不同线段的各一个端点连接所在直线与 \(x\) 轴负半轴的交点，假设两个端点都是下端点，记为 \(R_1,R_2\)，且 \(R_1\) 所在线段 \(x\) 坐标较小，考察射线 \(LR_1,LR_2\)，当 \(L\) 向左移动经过 \(R_1R_2\) 所在直线与 \(x\) 轴的交点时，\(LR_1\) 会从 \(R_2\) 的上方下来，贡献 \(-1\)，而 \(LR_2\) 会从 \(R_1\) 的下方上去，贡献 \(+1\)，则分别讨论上下端点与符号即可，注意到一定是同号才有可能行，共计 \(8\) 种情况，而可以通过将 \(y\) 轴负半轴的线段翻到正半轴区（按 \(x\) 轴轴对称），发现贡献是一致的，可以变为 \(4\) 种情况。

将下端点认定为 \(2k\) 而对应上端点认定为 \((2k+1)\) 即可更好实现，时间复杂度为 \(\mathcal{O}(n^2\log_2 n)\)。

Question 12. 「JOI 2015 Final」舞会

\(N\) 个贵族站在一排，第 \(i\) 个贵族的舞蹈的熟练度为 \(D_i\)，接下来执行如下操作：

• 看这一排中的前三个贵族，找出其中熟练度最大且编号最小的，与熟练度最小且编号最小的，让这两个一组，最后剩下的一个让其去这一排的末尾。

\(N\) 为奇数，所以最终总是剩下一个贵族，这个贵族就可以和公主 Sophenia 跳舞，我们希望这个贵族的舞蹈熟练度尽可能大。

为了达到这个要求，你可以在初始时任意排列一些贵族，其中 \(M\) 位贵族初始时要站在特定位置，其余随意，求出最后的贵族的舞蹈熟练度的最大值。

\(N\leq 99999, D_i\leq 10^9\)

---

设 \(D_i\) 只包含两个数，分别设为 \(x, y (x\ge y)\)，考察三个贵族：

• 若 \(x\) 出现 \(3\) 次，剩下 \(x\)。
• 若 \(x\) 出现 \(2\) 次，剩下 \(x\)。
• 若 \(x\) 出现 \(1\) 次，剩下 \(y\)。
• 若 \(x\) 出现 \(0\) 次，剩下 \(y\)。

如果不只包含两个数，我们可以考虑枚举值 \(v\)，如果 \(D_i\ge v\) 那么值 \(1\)，否则值为 \(0\)，然后用这个 \(0/1\) 序列跑上面的操作，最后看能不能剩下一个 \(1\)，是等价的问题。

接下来，考察操作，我们令一次操作是将这个贵族放到 \(N+1\) 位置，然后 \(N\gets N + 1\)。

那么每一个位置是选择了哪三个贵族是固定的，与熟练度无关，这个形成三叉树型结构。

考虑树形 DP，设 \(f_i\) 表示让树的结点 \(i\) 得到 \(1\)，最少需要几个 \(1\)。

• 初始值为叶子结点。
  • 如果结点的值确定了，那么如果 \(D_i\geq v\) 则为 \(0\)，否则为 \(+\infty\)。
  • 否则，值为 \(1\)。
• 转移为非叶子结点，根据上述，至少要有 \(2\) 个 \(1\) 才可以，设 \(3\) 个儿子得到的 DP 值分别为 \(x,y,z\)，那么这个点的 DP 值为其中最小值加上次小值。

最后去比较根节点的 DP 值与剩下的 \(1\) 的数量即可，这一次 DP 的复杂度为 \(\mathcal{O}(N)\)，已知 \(v\) 有 \(\mathcal{O}(N)\) 种选择，所以时间复杂度为 \(\mathcal{O}(N^2)\)。

能够发现这个东西具有单调性，考虑二分 \(v\)，时间复杂度优化至 \(\mathcal{O}(N\log_2 V)\) 或 \(\mathcal{O}(N\log_2 N)\)。