2024 Sept
Question 1. 「LAOI-6」Yet Another Graph Coloration Problem
给定一张 \(n\) 个点 \(m\) 条边的简单无向图,求是否存在一个点的黑白染色方案使得:
- 两种颜色的点都至少各有一个。
- 任意两个颜色不同的点之间都有至少 \(2\) 条不同的简单路径。
\(n,m\leq 2\times 10^5, \sum n, \sum m\leq 2\times 10^6\)
首先不连通肯定无解,这个先判掉。
考虑连通的时候什么时候会无解,可以发现树肯定无解,因为树的一个重要性质是“任意两个点之间有唯一的简单路径”,在环上,只要两个点之间的简单路径会经过环上的边,那么肯定有至少 \(2\) 条简单路径。
换句话说,边双内的两个点之间一定有至少 \(2\) 条简单路径,考虑边双缩点后形成的树。
选择一个大于 \(1\) 的边双,从该边双内选择一个点 \(u\),并将该边双通过 \(u\) 节点连出的子树内的所有边双染成一种颜色,其余点染成另一种颜色。
此时两个异色点肯定会跨边双,故一定有至少 \(2\) 条简单路径。
Question 2. 【MX-X3-T3】「RiOI-4」GCD 与 LCM 问题
给定正整数 \(a\),求出正整数 \(b,c,d\) 满足 \(a+b+c+d = \gcd(a,b) + \operatorname{lcm}(c,d)\)
\(T\leq 2\times 10^6, a\leq 10^9\),要求 \(b,c,d\leq 1.7\times 10^9\)。
令 \(b=1\),即有 \(\operatorname{lcm}(c,d) - c - d = a\),考虑 \(f(c,d) = \operatorname{lcm}(c,d) - c - d\) 的性质。
从 \(a\) 为奇数开始,如果令 \(c = 2\) 而 \(d\) 为另一奇数,则 \(f(c,d) = 2d - 2 - d = d - 2\),可以遍取所有奇数。
如果令 \(c = 4\) 而 \(d\equiv 2 \pmod 4\),则 \(f(c,d) = 2d - 4 - d = d - 4\),可以遍取所有满足模 \(4\) 为 \(2\) 的数字。
归纳有:令 \(c = 2^k\) 而 \(d\equiv 2^{k-1} \pmod {2^k}\),则 \(f(c,d) = d - 2^k\),可以遍取所有正整数 \(a\)。
此时上限为 \(1.5\times 2^{30}\leq 1.7\times 10^9\)。
Question 3. [Open Cup XXII Stage 2] M. Math
给定一个长度为 \(n\) 的正整数序列 \(a\),求有多少个 \((i,j)\) 满足 \(a_i^2 + a_j\) 是完全平方数。
\(n, a_i\leq 10^6\)
令 \(a_i^2 + a_j = (a_i + t)^2\),则有 \(a_j = 2a_i + 1 + 2a_i + 3 + \cdots \leq 10^6\),故枚举 \(a_i, t\) 的值暴力即可。
时间复杂度是对的,具体是多少不想算了。
Question 4. [Open Cup XXII Stage 2] A. AND
给定一个长度为 \(n\) 的非负整数序列 \(b\),构造一个序列长度不超过 \(5n\) 的非负整数序列 \(a\) 使得 \(a\) 的连续子序列 AND 的值集合为 \(b\)。
\(n\leq 2\times 10^5, b_i < 2^{20}\)
发现一个问题,就是 \(b\) 的最小值一定会是其它所有值的 AND,反证法显然。
所以把 \(b\) 中元素排个序,相邻两个数之间插一个最小值即可完成构造。
Question 5. [Open Cup XXII Stage 2] E. Eulerian?
给定一个 \(n\) 个点的有向连通图 \(G\),通过不超过 \(60\) 次以如下格式构造的询问判定 \(G\) 是否具有欧拉回路。
- 选择一个点集 \(S\),交互库给出 \(S\) 的导出子图的边数。
\(n\leq 10^4, m\leq 10^5\)
人类智慧交互问题。
首先第一次询问我们能够找出图的边数 \(m\)。
接下来,我们按照如下操作执行 \(29\) 轮:
- 对于每个点 \(u\),等概率随机将其划分至点集 \(A\) 与点集 \(B\),并分别询问 \(A,B\),如果 \(A,B\) 之间的边数不为偶数则无解。
证明:即判定是否每个点的度数都是偶数。
点的度数为偶数,则点的度数和为偶数,两端点处于同一点集的边为该点集提供 \(2\) 的点度和,处于不同点集的边各提供 \(1\) 的点度。
所以为奇数时一定无解,如果为偶数且存在某些点的点的度数为奇数,将这个点换一个点集则改变奇偶性,因此正确率为 \(\dfrac{1}{2}\)(奇数偶数一一对应)。
\(29\) 次询问后,错误率为 \(\dfrac{1}{2^{29}}\)。
Question 6. [Open Cup XXII Stage 2] F. Fancy Formulas
给定质数 \(p\),有 \(q\) 次询问,给定两个数对 \((a,b),(c,d)\),判断最少要几步才能将 \((a,b)\) 转化为 \((c,d)\),操作方式为:
- 将 \((a,b)\) 在模 \(p\) 意义下替换为 \((2a,b-a)\)。
- 将 \((a,b)\) 在模 \(p\) 意义下替换为 \((a-b,2b)\)。
\(p\leq 10^9+7, q\leq 10^5, 0\leq a,b,c,d < p\),保证 \(a+b\) 不是 \(p\) 的倍数。
发现操作后 \(a+b\) 的值在模 \(p\) 意义下不变,于是大胆猜测有无解仅当 \(a+b\) 与 \(c+d\) 是否同余。
即在 \(a+b \equiv c+d \pmod p\) 时构造解。
假设 \(s = a+b\),然后将 \(a,b,c,d\) 全部除以 \(s\),则操作数不变。
于是我们从 \((a,1-a)\) 出发,每一次操作我们将 \(a\) 替换成 \(2a\) 或 \(2a-1\),请问达到 \(c\) 的次数为?
发现每一次操作将 \(a\) 能够达到的范围翻倍,于是答案在 \(\mathcal{O}(\log_2 p)\) 范围,枚举即可。
Question 7. [Open Cup XXII Stage 2] H. Hamiltonian
构造一个不超过 \(20\) 个点的简单无向图,使得恰好存在 \(k\) 个无序点对 \((u,v)\) 使得 \(u,v\) 之间有哈密顿路径。
\(k\leq 60\)。
首先 \(k=1, k=2\) 需要特殊构造,把样例 Copy 下来即可。
当 \(3\leq k\leq 20\) 的时候,构造一个大小为 \(n\) 的环即可。
接下来,我们考虑两个特殊的结构:
- \(K_n\),即 \(n\) 个点的完全图,带来 \(\dfrac{n(n-1)}{2}\) 个点对。
- \(C_n\),即 \(n\) 个点的环,带来 \(n\) 个点对。
考虑让 \(K_x\) 与 \(C_y\) 共一条边,则有 \(\dfrac{x(x-1)}{2} + 2(x-1) + (y-2)\) 个点对,此时 \(x\ge 3, y\ge 4\),枚举一下构造即可。
Question 8. 【MX-X4-T3】「Jason-1」数对变换
给定两个正整数数对 \((a,b),(c,d)\),请判断能否通过如下操作将 \((a,b)\) 转化为 \((c,d)\),如果能,请在 \(65\) 步以内构造解。
- 选择 \(1\leq k\leq a\),将 \((a,b)\) 转化为 \((\lfloor{\frac{a}{k}}\rfloor,bk)\)。
- 选择 \(1\leq k\leq b\),将 \((a,b)\) 转化为 \((ak,\lfloor{\frac{b}{k}}\rfloor)\)。
\(a,b,c,d\leq 10^9, T\leq 10^4\)。
一个整除,一个乘,则 \(ab\) 的值不会增加,所以若 \(ab < cd\) 则无解。
如果 \(cd=1\),手动模拟可以发现如果 \(ab > 1\) 则 \(ab\) 最小达到 \(2\),也需要特判。
若 \(ab=cd\),则可以通过 \(2\) 次操作完成。
每一次操作可以将 \(ab\) 减去 \((a\bmod k) b\) 或者减去 \((b\bmod k)a\),考虑 \(k\) 从 \(\lfloor{\frac{b}{2}}\rfloor +1\) 开始一路取到 \(b\),则余数的变化是连续的最小的若干非负整数,所以每次尽可能的将 \(ab\) 减小即可。
Question 9. 【MX-X4-T4】「Jason-1」一步最优
给定一个长度为 \(n\) 的整数序列,考虑如下问题:
- 选择至多 \(m\) 个不交区间,最大化所有区间的元素和的和。
考虑如下错误贪心算法:
- 执行如下操作 \(m\) 次:
- 每次随便选出一个与先前选出区间不交的子段和尽可能大的区间。
请问:\(\forall 1\leq i\leq n, m=i\) 时这个贪心算法得到答案的最小值与最大值。
\(n\leq 10^5, -10^9\leq a_i\leq 10^9, \sum n\leq 5\times 10^5\)
可以发现:答案取到最小值时每次取出的区间是极长的,取到最大值时时极短的。
证明:相当于把一段和为 \(0\) 的区间拼接到某一次选择中,这样会少几个正数的贡献。
接下来可以证明:两个同时极长(或极短)的区间不会交。
证明:否则两个区间的并(或交)也一定是极长(或极短)的。
那么就很简单了,用 set 维护剩余区间,每次取出最大子段和最大(且 \(> 0\))的一个区间,取出其中极长的一段或者极短的一段即可。
维护极长的最大子段和与极短的最大子段和也是容易的,于是时间复杂度为 \(\mathcal{O}(n\log_2 n)\)。
Question 10. [Open Cup XXII Stage 2] G. Glory Graph
给定一张 \(n\) 个点的完全图,边有黄色与蓝色两种颜色。我们为 \(4\) 个不同的点 \((u,v,w,x)\) 导出的完全子图进行分类:
- A 类:\(4\) 个点导出的 \(6\) 条边中有恰好 \(5\) 条颜色相同。
- B 类:\(4\) 个点导出的 \(6\) 条边中有恰好 \(3\) 条黄边,\(3\) 条蓝边,且不存在同色三角形。
求 B 类图数量 - A 类图数量 的值。
\(4\leq n\leq 2000\)
What can I say... nb 问题。
首先,\(4\) 个点导出的本质不同的完全子图只有 \(6\) 种,即这 \(6\) 种两两不同构:
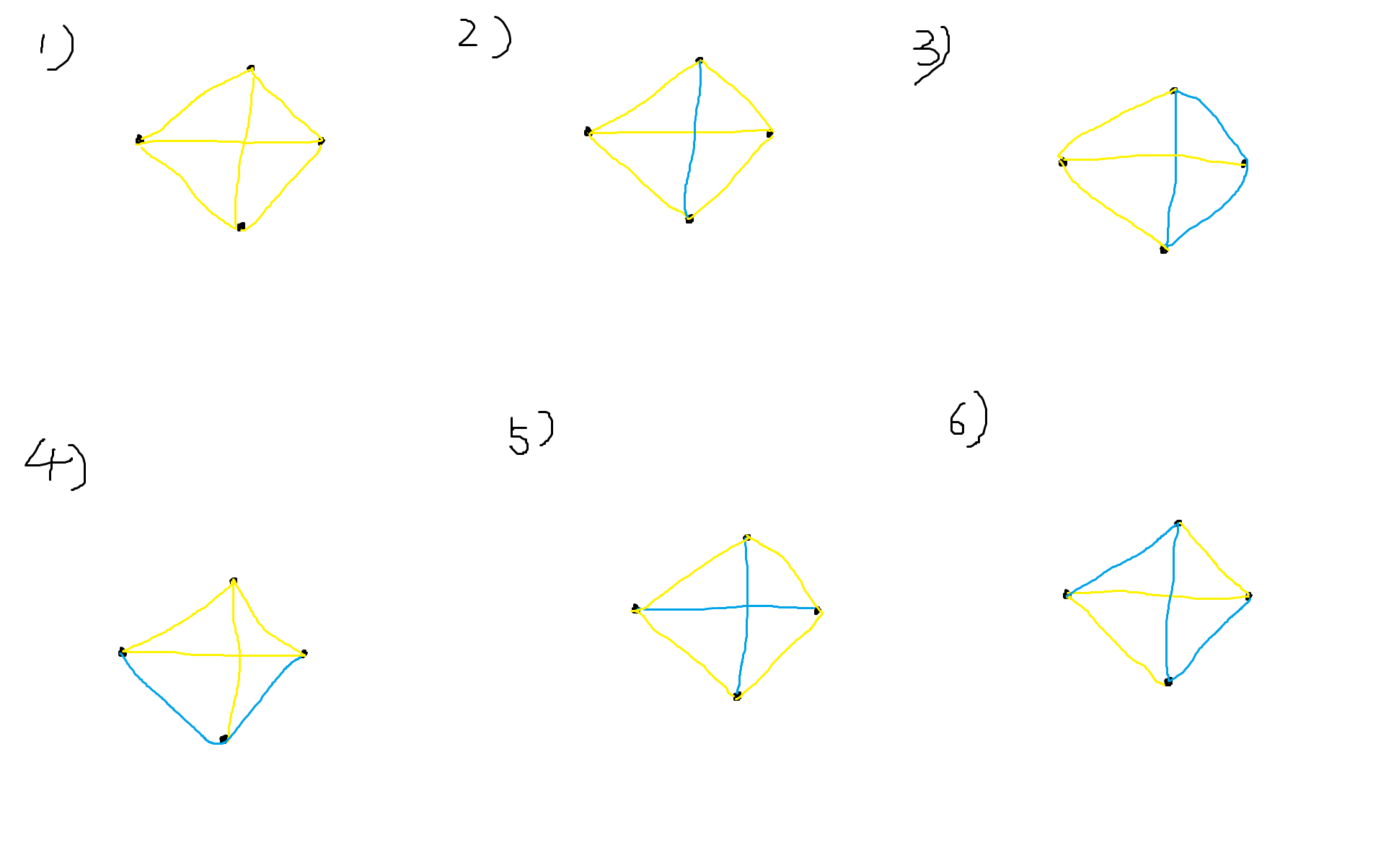
我们记上述 \(6\) 种图的数量分别为 \(x_1, x_2, x_3, x_4, x_5, x_6\),我们的目标是 \(x_6 - x_2\),接下来我们要凑数字了。
- 我们尝试计算出 \(P_1\) 表示选出 \(4\) 个点的完全子图的方案数,则有 \(P_1 = \binom{n}{4} = \dfrac{n(n-1)(n-2)(n-3)}{24}\),等价于 \(x_1 + x_2 + x_3 + x_4 + x_5 + x_6\),记 \(C_1 = P_1\)。
- 我们尝试计算出 \(P_2\) 表示选出 \(4\) 个点 \((A,B,C,D)\) 构成完全子图,且 \(AB,BC\) 不同色的方案数,记 \(b_i,y_i\) 表示与点 \(i\) 以蓝边、黄边连出的点的数量,则有 \(P_2 = (n-3)\overset{n}{\underset{i=1}{\sum}} 2b_iy_i\),同时思考 \(P_2\) 的意义,等价于 \(0x_1 + 8x_2 + 12x_3 + 12x_4 + 16x_5 + 16x_6\),记 \(C_2 = \dfrac{P_2}{4}\)。
- 我们尝试计算出 \(P_3\) 表示选出 \(4\) 个点 \((A,B,C,D)\) 构成完全子图,且 \(AB,BC,CD,DA,AC\) 同色的方案数,记 \(f_{i,j}\) 表示对边 \((i,j)\) 满足 \((i,j),(i,k),(j,k)\) 同色的点 \(k\) 的方案数,则有 \(P_3 = \underset{1\leq i < j\leq n}{\sum} 2f_{i,j}(f_{i,j}-1)\),同时思考 \(P_3\) 的意义,等价于 \(24x_1 + 4x_2 + 0x_3 + 0x_4 + 0x_5 + 0x_6\),记 \(C_3 = \dfrac{P_3}{4}\)。
- 我们尝试计算出 \(P_4\) 表示选出 \(4\) 个点 \((A,B,C,D)\) 构成完全子图,且 \(AB,BC,CD,DA\) 同色并与 \(AC\) 异色的方案数,记 \(g_{i,j}\) 表示对边 \((i,j)\) 满足 \((i,k),(j,k)\) 同色且与 \((i,j)\) 异色的点 \(k\) 的方案数,则有 \(P_4 = \underset{1\leq i < j\leq n}{\sum} 2g_{i,j}(g_{i,j}-1)\),同时思考 \(P_4\) 的意义,等价于 \(0x_1 + 4x_2 + 0x_3 + 0x_4 + 8x_5 + 0x_6\),记 \(C_4 = \dfrac{P_4}{4}\)。
回顾一下,我们有:
- \(C_1 = x_1 + x_2 + x_3 + x_4 + x_5 + x_6\)
- \(C_2 = 2x_2 + 3x_3 + 3x_4 + 4x_5 + 4x_6\)
- \(C_3 = 6x_1 + x_2\)
- \(C_4 = x_2 + 2x_5\)
我们的目标是 \(x_6 - x_2\),考虑构造关于 \(C_1,C_2,C_3,C_4\) 的一次代数式得到,记系数分别为 \(X_1,X_2,X_3,X_4\),对 \(x_1,x_2,x_3,x_4,x_5,x_6\) 的目标系数列出方程组:
解得:
则有 \(x_6 - x_2 = -3C_1 + C_2 + \dfrac{1}{2}C_3 - \dfrac{1}{2}C_4\),其中 \(f,g\) 可以用 bitset 简单求解,时间复杂度为 \(\mathcal{O}(\frac{n^3}{\omega})\)。
Question 11. [Open Cup XXII Stage 2] D. Deleting
给定一个序列 \(A = \{1,2,\cdots, n\}\),每一次你可以选择两个相邻的数字 \(x,y\),删除它的代价是 \(c(x,y)\),保证 \(n\) 为偶数,则在 \(\frac{n}{2}\) 次操作后可以将数列清空,所有操作的代价是单次操作代价的最大值,请问清空序列的最小代价。
\(n\leq 4000\) 且 \(c(x,y)\) 是 \(1\) 到 \((\frac{n}{2})^2\) 的全排列。
题解的方法非常高手,但是可以简单一点。
最大值最小化,首先考虑二分答案 \(val\),即只通过不超过 \(val\) 的代价的操作能否清空序列。
记 \(f_{l,r}\) 表示能否清空 \([l,r]\),然后转移显然,倒序枚举 \(l\),顺序枚举可行的 \(r\),然后若 \(a_{l,r}\leq val\) 且【\(r=l+1\) 或者是 \(f_{l+1,r-1}\) 可以删空】则可行。
如果 \(f_{l,r}\) 可行,则 \(f_{r+1,k}\) 可行一定有 \(f_{l,k}\) 可行,这里类似于或运算,bitset 优化即可。
一个加速的方法是每个 \(l\) 所对应的 \(r\),整除 \(2\) 也不会重复,所以直接改为存储 \(\frac{r}{2}\) 即可加速。
时间复杂度为 \(\mathcal{O}(\frac{n^3\log_2 n}{\omega})\),反正是能过的。
Question 12. [Open Cup XXII Stage 2] B. Bruteforce
给定一个长度为 \(n\) 的非负整数序列 \(A\),维护 \(q\) 次操作:
- 单点修改,将 \(A_p\) 修改成 \(x\),然后计算 \(w(A)\) 的值:
- 记 \(B\) 表示 \(A\) 升序排序后的结果,计算 \(\overset{n}{\underset{i=1}{\sum}} \Big\lfloor{\dfrac{B_i\times i^k}{w}}\Big\rfloor\),答案对 \(998244353\) 取余。
其中 \(k,w\) 是给定正整数,对每次计算都是一样的。
\(n,q\leq 10^5, A_p,x\leq 10^5, k,w\leq 5\)
值域不大,并且基于升序排序的结果,果断考虑权值线段树,考虑如何计算答案。
根据我们所知的,\(\Big\lfloor{\dfrac{a}{b}}\Big\rfloor = \dfrac{a - a\bmod b}{b}\),而 \(w\) 是固定的,所以我们要计算两个问题:
\(\overset{n}{\underset{i=1}{\sum}} B_i\times i^k\),减去 \(\overset{n}{\underset{i=1}{\sum}} (B_i\times i^k \bmod w)\),然后乘上 \(w\) 的逆元。
这里直接贴 \(1\sim 5\) 的逆元了:\([1,499122177,332748118,748683265,598946612]\)。
首先考虑一个问题:权值线段树上是不好直接处理下标的,我们更容易处理的是每个子树的大小。
考虑式子 \(2\),我们可以对每个子树计算 \(cnt_{u,x,y}\) 表示 \(u\) 节点子树中值 \(\equiv x \pmod w\) 并且位置(下标从 \(1\) 开始) \(\equiv y \pmod w\)(注意重复值的影响),重点是合并信息。
下记 \(u\) 表示目前节点,\(l\) 表示左儿子,\(r\) 表示右儿子。
令左子树大小为 \(\text{shift}\),则右子树的每个元素的下标都要向后移动 \(\text{shift}\) 位,故 \(cnt_{u,x,y}= cnt_{l,x,y} + cnt_{r,x,y-\text{shift}}\),在 \(\bmod\) 意义下做减法,单次合并时间复杂度为 \(\mathcal{O}(w^2)\)。
考虑式子 \(1\),我们可以对每个子树计算 \(f_{u,t}\),表示该子树内从 \(1\) 下标开始的位置时 \(\overset{n}{\underset{i=1}{\sum}} B_i\times i^t\) 的值,提醒一下 \(t\) 是 \(i\) 的指数。
考虑信息的合并,还是令左子树大小为 \(\text{shift}\),则右子树的每个元素的下标都要向后移动 \(\text{shift}\) 位,故:
则单次合并时间复杂度为 \(\mathcal{O}(k^2)\)。
单点修改是容易的,每次计算答案,式子 \(1\) 就是 \(f_{1,k}\),式子 \(2\) 枚举 \(cnt_{1,x,y}(0\leq x,y < w)\) 减掉即可,不要忘记乘逆元。
最终时间复杂度为 \(\mathcal{O}((n+q)(k^2+w^2)\log_2 V)\),其中 \(V\) 表示元素值域有 \(V = 10^5\)。
Question 13. [ARC184B] 123Set
给定正整数 \(N\),令 \(S_x=\{x,2x,3x\}\),求一个集合 \(T\),使得 \(\{1,2,\cdots,N\}\subseteq \underset{x\in T}{\bigcup} S_x\),最小化 \(|T|\)。
\(1\leq N\leq 10^9\)
设 \(X = 2^x3^yz\),其中 \(x,y\) 均为自然数,然后按照 \(z\) 分类,视 \((x,y)\) 为坐标。
接下来我们有若干个这样的问题等待解决:
- 给出 \(N\) 行的阶梯图,第 \(i\) 行只有最左边 \(r_i\) 个格子,每次你可以选择一个 \((x,y)\) 并同时覆盖 \((x,y),(x+1,y),(x,y+1)\),请问最少需要选择多少个位置才可以覆盖完全部阶梯格子,格子可以重复覆盖,可以覆盖出界,\(N\leq 31, r_i\leq 19\)。
状压即可,设 \(f_{i,S}\) 表示当前考虑到第 \(i\) 行且覆盖状态为 \(S\),枚举状态向 \(f_{i+1,T}\) 转移,采用高维后缀 \(\min\) 即可在 \(\mathcal{O}(Nr_i2^{r_i})\) 复杂度内求解一组问题。
但是这样可能较慢,我们发现,对于一组平面,格子是按照一定顺序被加入的。
也就是说:如果两个问题的格子数量是相同的,则格子的排布形态也一定是相同的,则答案就会是相同的。
一次不可能有超过 \(400\) 个格子,本地打表即可,时间复杂度为 \(\mathcal{O}(N)\)。


