OO第一单元总结
一、程序架构分析
(一)、总体设计思路
第一单元的内容为表达式的化简。化简涉及到两个关键过程:解析字符串,计算(也就是化简)字符串。
根据给出的形式化表述,在化简过程中涉及到的对象总可以划归到三类:表达式、项和因子(当然,其中因子类还会在之后包含自定义函数、求和函数等需要特别处理的类)。也就是说,从宏观上来看,我们只需建立这三种类,并分别实现对应的解析字符串、计算字符串方法,而后即可通过他们间的相互调用来完成整个表达式的计算化简。
在三次作业的迭代开发中,都遵循以上思路。下面逐次分析三次作业的具体架构实现,辅以代码度量分析、UML图,并分析被测试出的BUG。
(二)、逐次作业架构分析
1、第一次作业
(1)、思路说明
第一次作业难度不高,但作为后两次作业的基石,也非常考验编程时的思想。
首先,第一次作业不存在三角函数,这意味着,我们化简的结果一定是一个多项式函数,而且题目限制这个多项式最高次为8,因此,可以很舒服地使用一个ArrayList来存储各次(0~8)的系数即可。
现在来看看如何实现我们在总体思路中提到的三个关键类及两个关键方法。
首先定义Computable类作为Expression\Term\Factor三个类的父类,其中定义了parsing\compute两个之前提到的关键方法,让子类重写。其还包含必要的用于计算的属性,及相关get\set方法。
下面分别对三个具体类的方法进行说明。
对Expression类,其解析目标为拆分出表达式中一个个项,计算目标为对于每个项的计算返回结果进行加减法处理;对Term类,其解析目标为拆分出一个个因子,计算目标为对于每个因子的计算返回结果进行乘法处理;对Factor类,在第一次作业中无需解析,计算目标也很简单,对于表达式因子,创建新的Expression对象,并返回该对象计算结果作为自身计算结果,对于常数项和幂因子,稍加处理即可返回正确结果。
在第一次作业中,由于括号嵌套不存在,所以可直接根据形式化表述写出三个类的正则表达式(需递推一次),匹配过程即为解析过程;计算过程则是简单的循环。
(2)、UML图
UML图如下(省略了getter、setter方法):
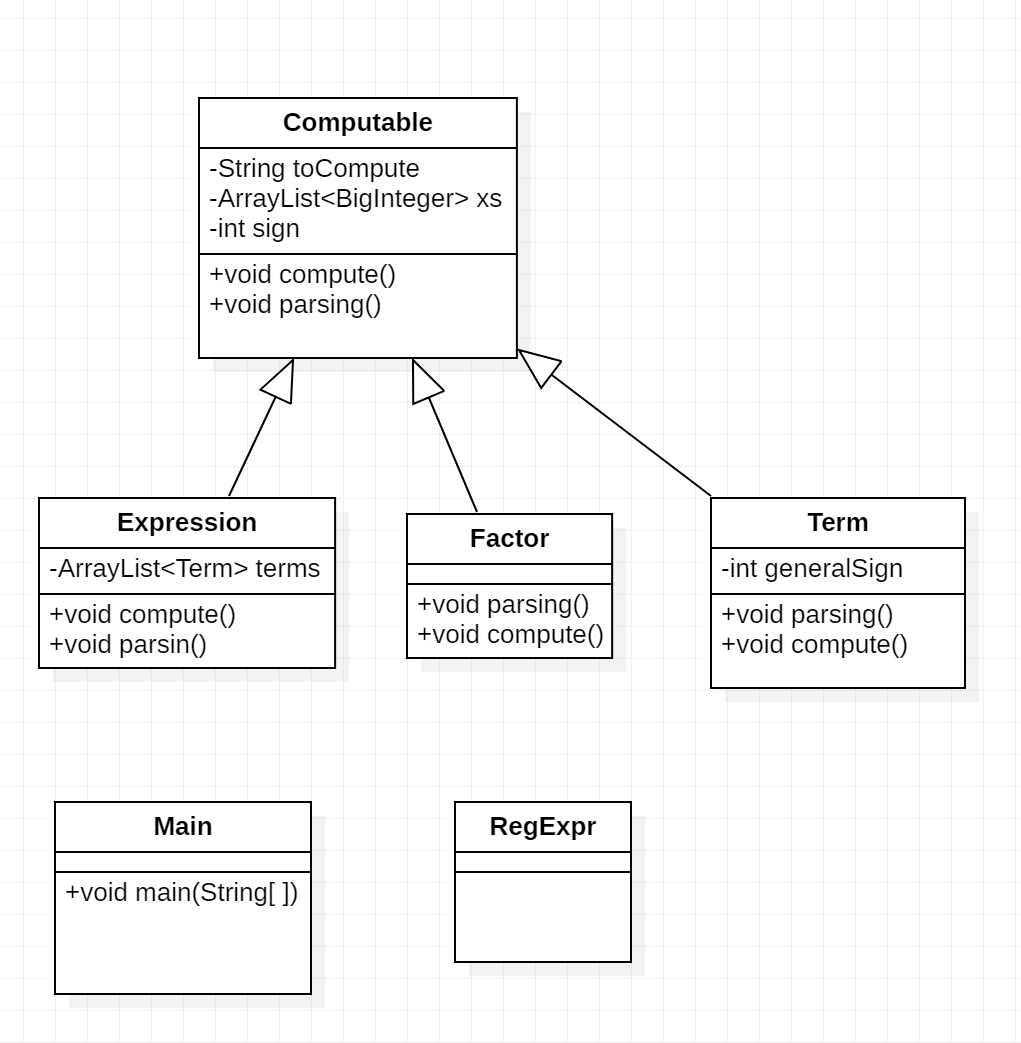
说明: 其中RegExpr类为存储相关正则表达式的类,只有getter方法及相关正则表达式字符串,此处不详细列出。
(3)、类复杂度分析
度量分析如下:
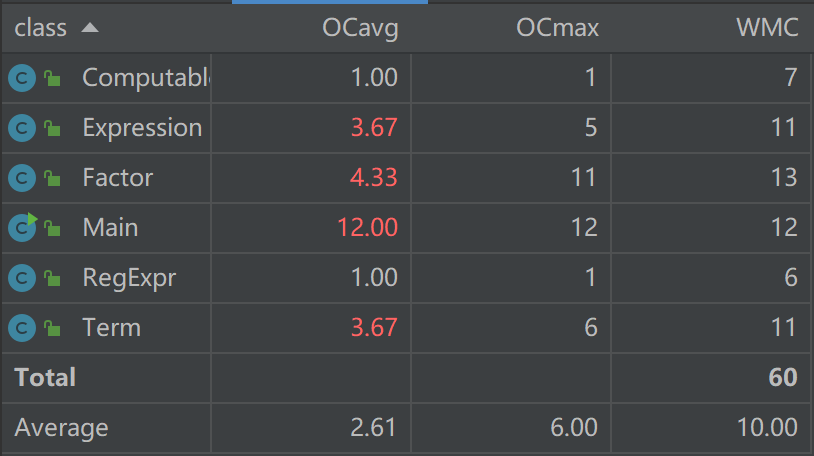
不得不承认,第一次作业类复杂度较高,这一方面是由于对题目理解还不够深刻,导致在符号处理、化简等问题上做得不够好,另一方面,编程水平还有待提高。
(4)、方法圈复杂度分析
度量分析如下:
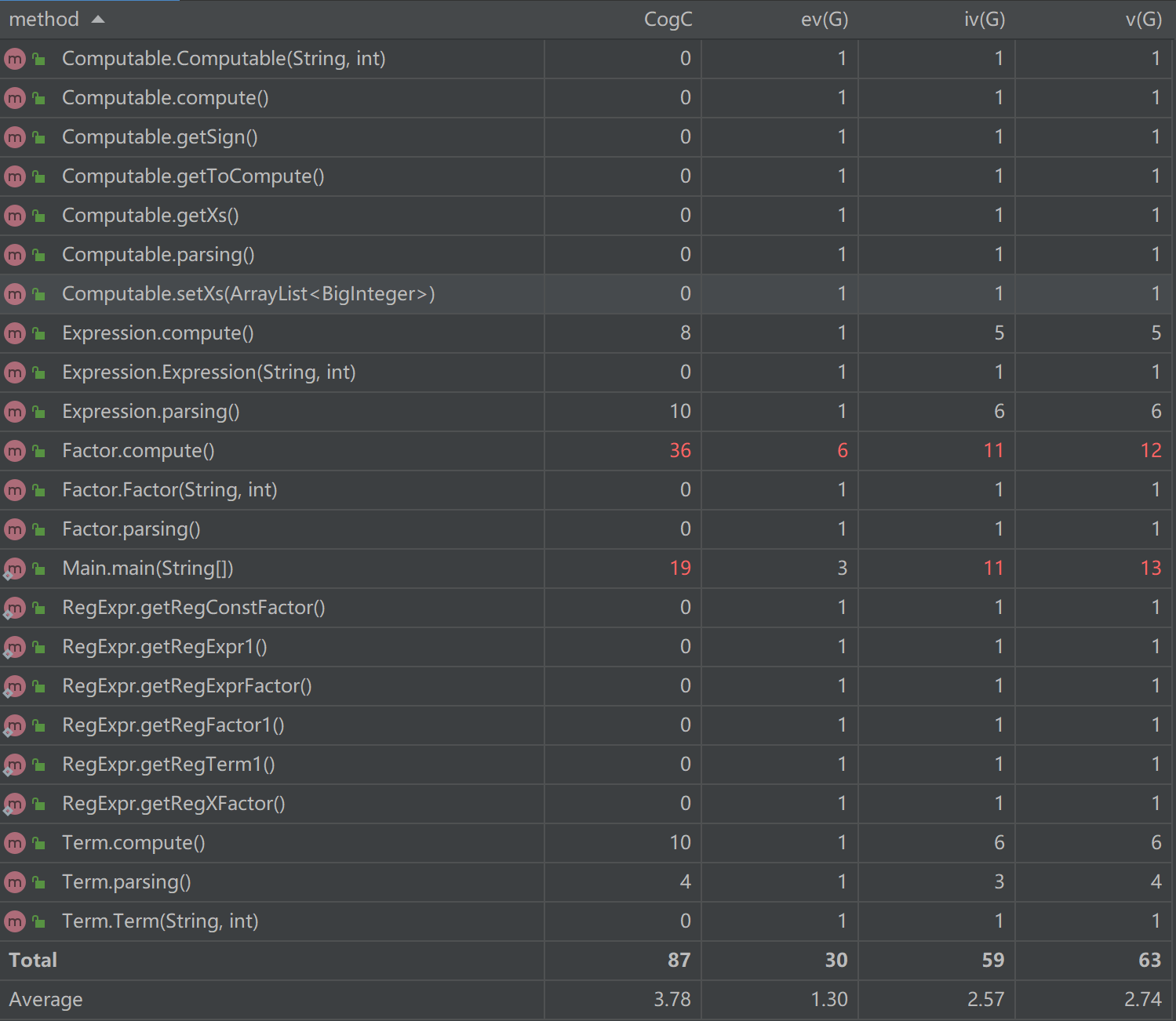
方法圈复杂度基本都在可接受范围内。其中Factor.compute()方法由于需处理多种不同因子和化简的情况,圈复杂度略高;Main.main(String[ ])方法也是由于需处理化简,圈复杂度略高。
2、第二次作业
(1)、思路说明
第二次作业主要变化有以下:
1、加入了三角函数,导致化简表达式不再是简单的多项式函数。
2、加入了自定义函数与求和函数,需要“安全地”进行字符串替换。
3、指数范围无限制。
分别应对方法如下:
1、利用HashMap<项,系数>存储化简结果。
2、对自定义函数和求和函数分别建立类,通过“安全地”进行字符串替换,再利用表达式类进行解析和计算。
3、用BigInteger存储指数信息。
下面说明具体实现要点:字符串如何才能实现“安全替换”?
由于第二次作业仍然限制了括号嵌套层数,因此,我们仍然使用正则表达式匹配的方法来完成表达式的解析,故我们字符串替换后只要满足形式化表述,能够与正则表达式相匹配即可。具体表现为:加括号后替换,但是删去三角函数内多余的一层括号。
由此,便在第一次作业的架构基础上完成了迭代开发。
(2)、UML图
UML图如下:
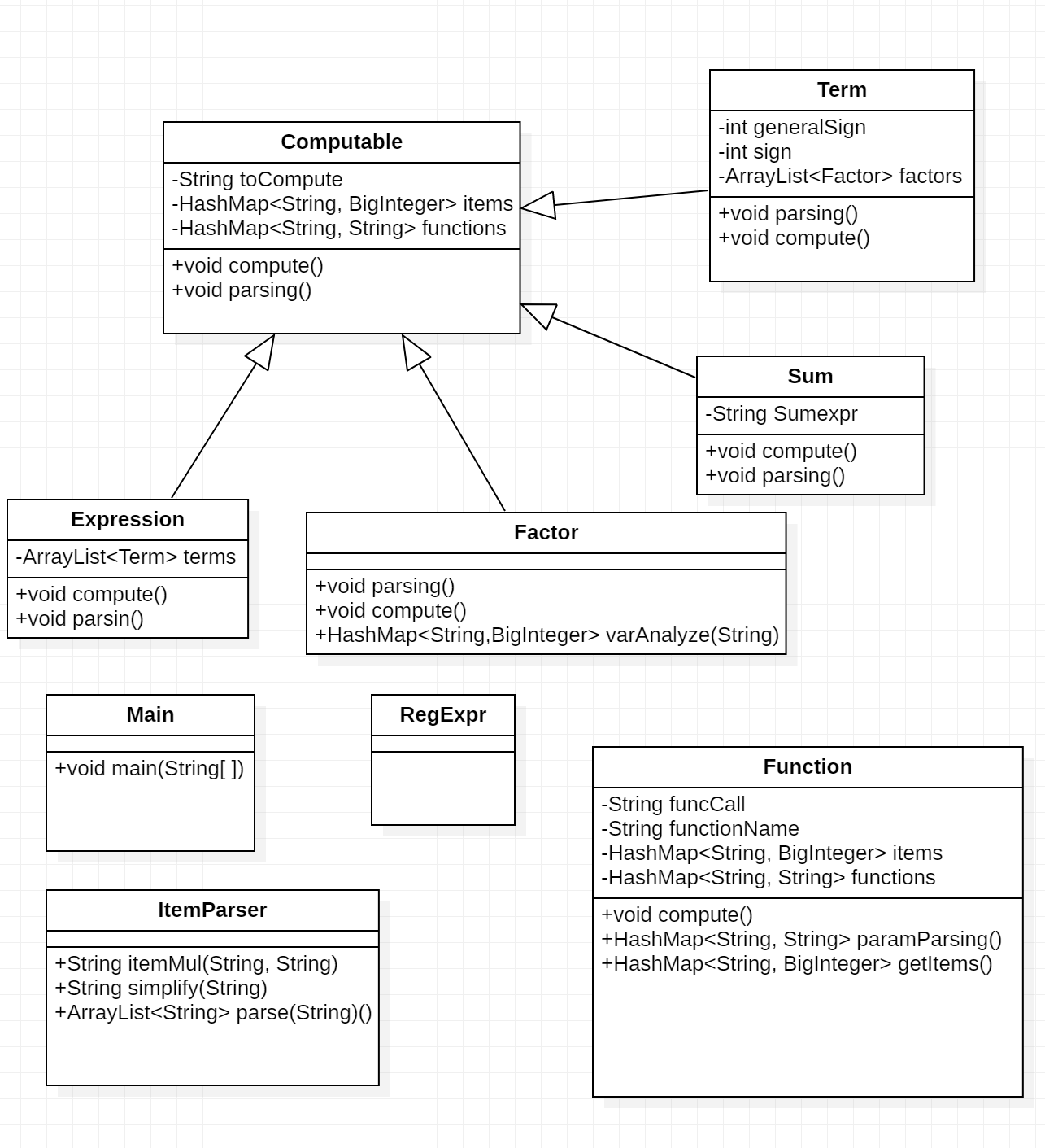
说明: 其中Function类、Sum类分别为自定义函数类、求和函数类,他们的parse方法为字符串替换,compute方法为调用Expression类完成计算。由于Function的特殊性,单独抽离作为一类。
ItemParser类为抽离出用于字符串“计算”的工具类,其主要作用为计算因子相乘的结果,并进行化简。
(3)、类复杂度分析
度量分析如下:
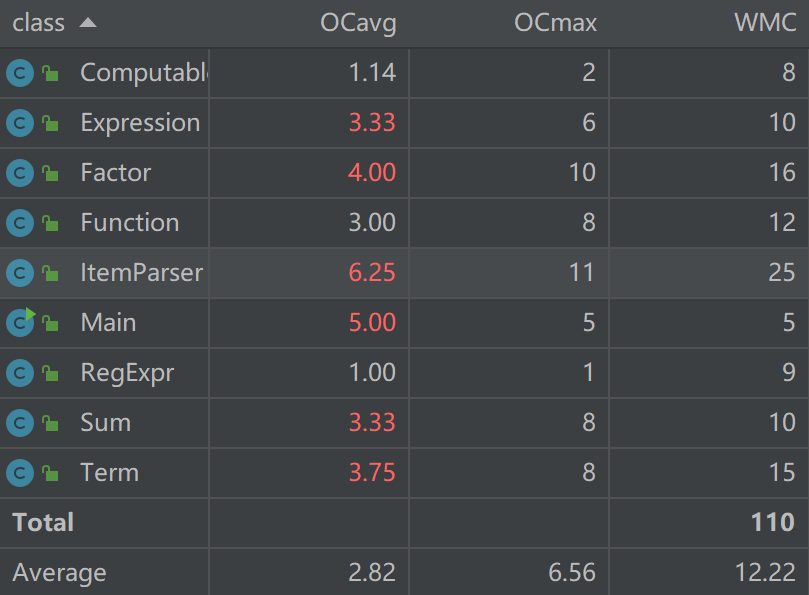
类复杂度仍然较高,主要问题在于正则表达式匹配难以完美地处理各种情况,需要手动编写分支逻辑进行;其次,化简时的各种判断也加剧了复杂度。
(4)、方法圈复杂度分析
度量分析如下:
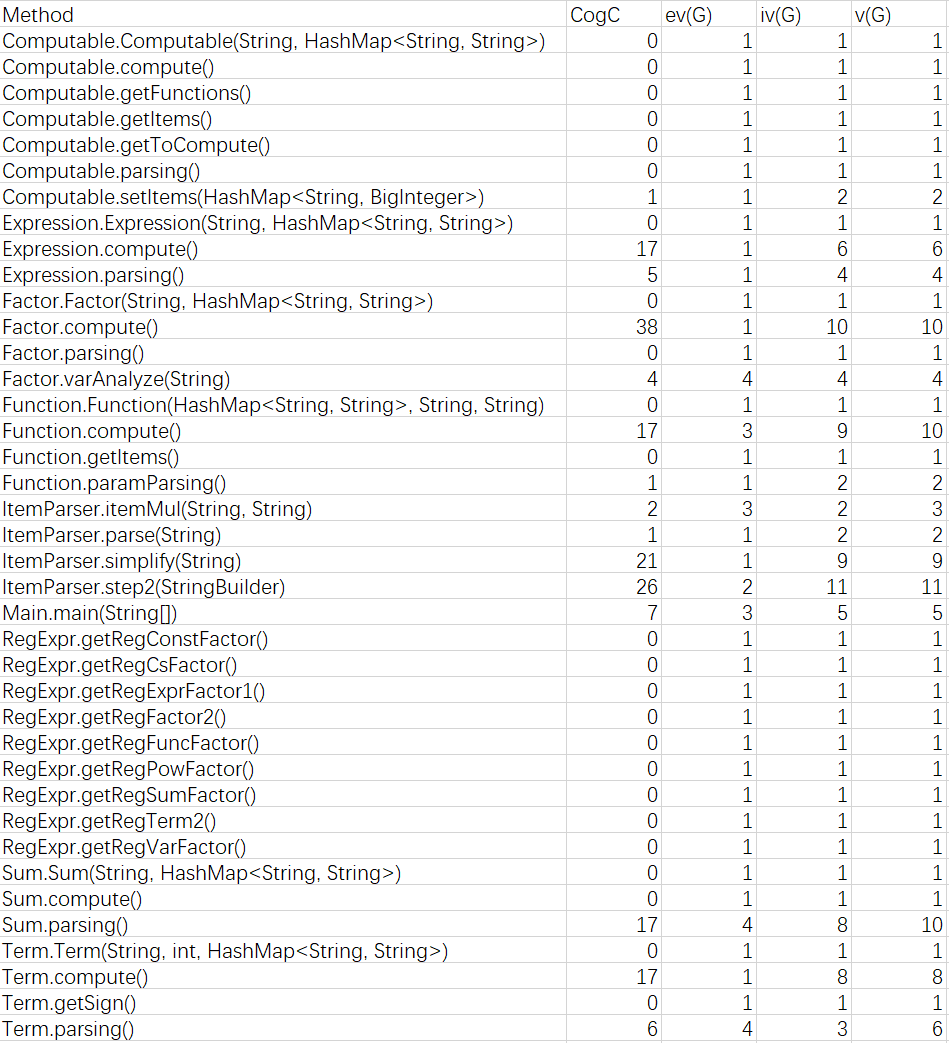
在分类判断因子,处理特殊情况以及化简时的复杂度较高,
3、第三次作业
(1)、思路说明
第三次作业的关键点只有一个:如何解决因子嵌套问题?只要解决这个问题,我们便可简单通过字符串替换来递归调用各个类,顺畅地完成计算。
通过分析在一二次作业中使用的架构,可以发现,因子嵌套给带来的最大,但幸运地,也是唯一问题在于:无法再使用正则表达式进行解析。
先分析正则表达式在哪里发挥作用:
1、将表达式分解为项
2、将项分解为因子
3、判断因子类型
下面给出对应解决思路:
1、利用正负号
2、利用乘号
3、非常简单,各种因子有各自明显特征,不再赘述
下面讲解如何利用正负号、乘号实现分解表达式、分解项。
首先总的原则:我们不考虑任何尚处于任意一层括号中的正负号及乘号,但不必担心,因为总会递归处理到他们。
那么对于表达式,其含有的不处于括号中的正负号只有以下几种可能:(记为集合1~4)
1、分割了项的正负号,也是我们的目标
2、每个项自身可带的正负号
3、常数因子可带的正负号
4、指数上的正号
可论证,一个正负号属于集合1,当且仅当,其前一个有效字符不是乘号或正负号。
证明略。(简单的分类讨论即可证明)
对于项,其含有的不处于括号中的乘号只有以下几种可能:(记为集合1~2)
1、分割了因子的乘号,也是我们的目标
2、指数上的乘号
可论证,一个乘号属于集合1,当且仅当,其前一个和后一个有效字符均不是乘号。
证明略。(简单的分类讨论即可证明)
至此,第三次作业可以说便被完全攻破,只需将正则表达式解析改为利用上面分类讨论的结论进行解析即可。其余总体架构可保持不变,只需根据题意增加小变化,例如增加对三角函数中因子的计算。
(2)、UML图
UML图如下:
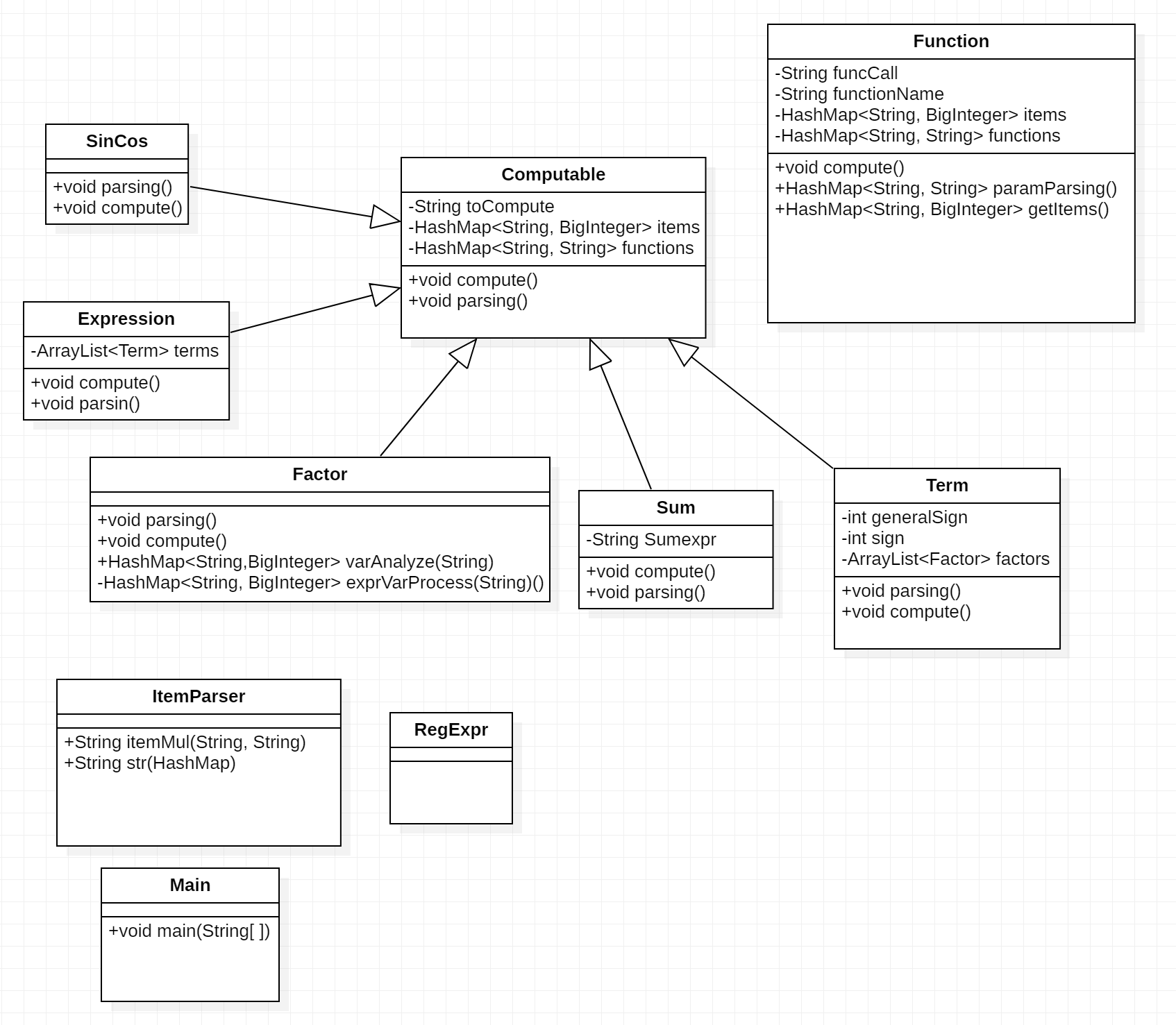
说明: 由于正则表达式还有小用处,因此RegExpr类并未删去。
(3)、类复杂度分析
度量分析如下:
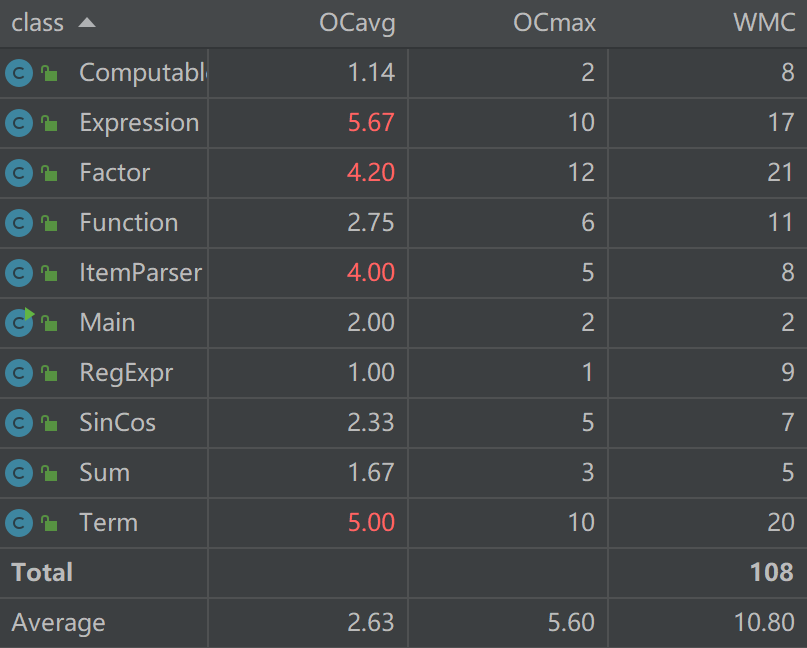
虽然个别类复杂度仍偏高,但总体相比第二次作业好了。主要是由于解析方法相比于正则表达式更具一般性,少了很多情况的判断。
(4)、方法圈复杂度分析
度量分析如下:
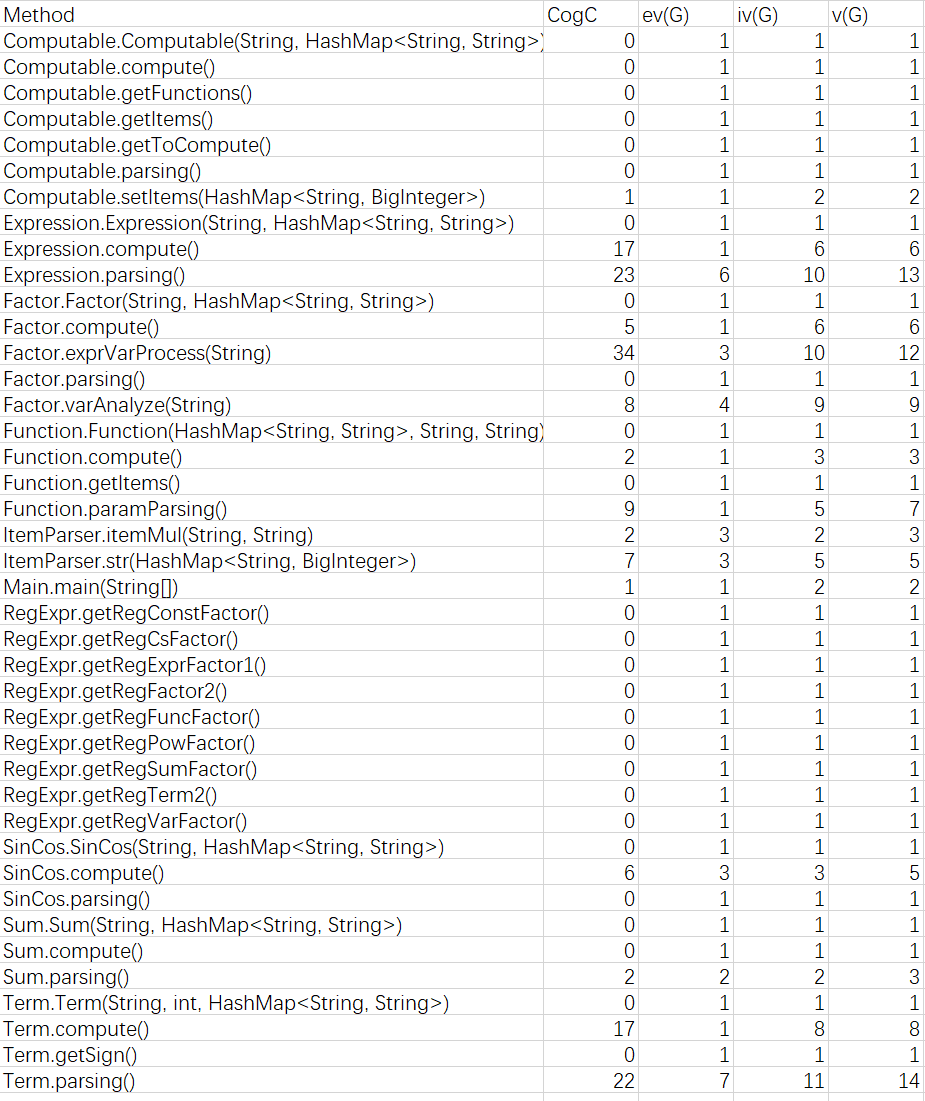
整体比之前有进步,尤其是考虑到第三次作业是更进一步的迭代开发。当然,仍有个别方法由于历史遗留问题具有较高复杂度,在今后编程过程中将尽力避免此类现象。
二、BUG分析
本单元中,一共出现了两次BUG。
第一次是在第一次作业中,原因是字符串访问下标越界,未考虑到指数上可能的加号。这是一个非常非常低级的BUG,有无数的数据可以测出这个BUG,这也导致了在之后的强测与互测中失了很多分。
反思: 一方面是编码问题,第一次用OO思想编写真正有意义的小型项目,确实会因为代码量,架构设计等问题感到紧张,犯低级错误。但另一方面也体现了测试的不上心,实际上本地测试若稍加用心便可避免这一BUG。希望今后不会再发如此低级错误。
第二次是在第二次作业中,原因是在化简表达式时,对于多个x零次幂相乘的情况处理疏忽,导致输出空串。
反思: 该BUG为逻辑性BUG,而且较为微小,不易在测试中测出,需要对代码的逻辑完备性进行分析才可发现。虽然在第二次作业中已经对化简表达式的功能进行了模块化,但思考上还是出现了不完备的情况,在今后编写代码的过程中一定要更加注意逻辑完备。
第三次作业虽然看起来最为复杂,但是在前两次作业的铺垫下,已经对题目有了深刻的理解,架构也足够完备,因此未出现BUG。
以上BUG均不会在代码行数和圈复杂度上带来变化,简单处理即可修复。
三、Hack相关
在本单元中,我并未进行过多Hack,只会用一些简单的特殊样例进行Hack。
当然,我很感谢认真Hack我,甚至可能认真阅读我代码的同学,是他们将我的程序变得更完善。
四、心得体会
作为OO的第一个篇章,本单元用难度可接受的题目引导我设计出了一个架构尚可的程序,整个架构的迭代开发过程在前文已有叙述,下面简单介绍我从中获得的一些体会。
首先是OO这种思想本身。现在的我肯定不能说已经学懂了OO,但确实可以体会到这一程序设计思想在开发中给我带来的帮助:有利于模块化、解耦,让设计的思维更加清晰。
其次是迭代开发中的一点感想。一个架构应该具有足够的抽象性,这么说或许本身就很“抽象”,但确实是我体会最深的一点。所谓抽象,就是架构应该让其上的每一部分(类、方法、属性、定义等)具备足够的自主性,同时简化隐藏繁琐的实现。当然,想做好是很难的,但是OO的思想或许可以帮助我们改善这一点。
最后是编码风格。经过这一单元,个人对于编码风格的重视更上一层楼。
五、结语
以上,便是本单元总结。


