李超线段树 学习笔记
Idea
主要用于动态维护一个线段或直线集合,支持在平面直角坐标系中插入一条线段或者直线,以及查询某一横坐标上的最值。
考虑在 x 轴上建立一棵线段树,每一个节点 \([l,r]\) 上维护的是在 \(x=\frac{l+r}{2}\) 上取最大值或最小值的一条直线(下面以插入直线,查询最大值为例)。
插入一条直线 \(B\) 时:
-
若当前节点上还没有直线,则直接将 \(B\) 放在当前节点。
-
若当前节点上已经有了一条直线 \(A\):
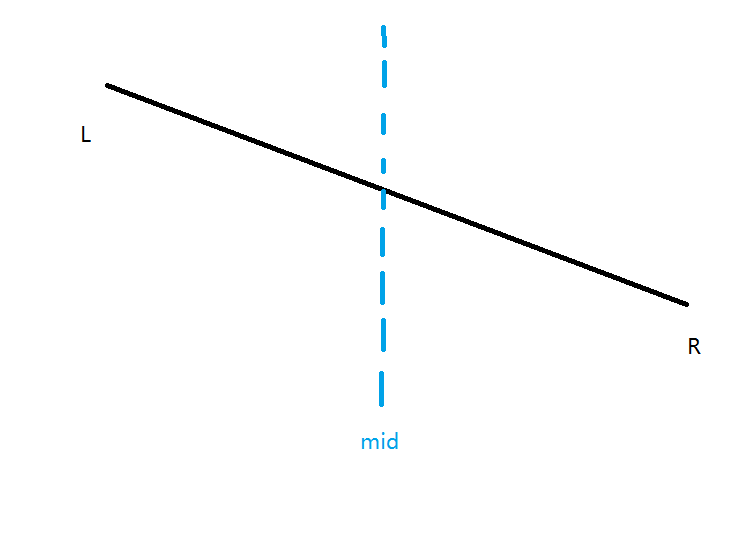
现在插入了一条直线 \(B\):
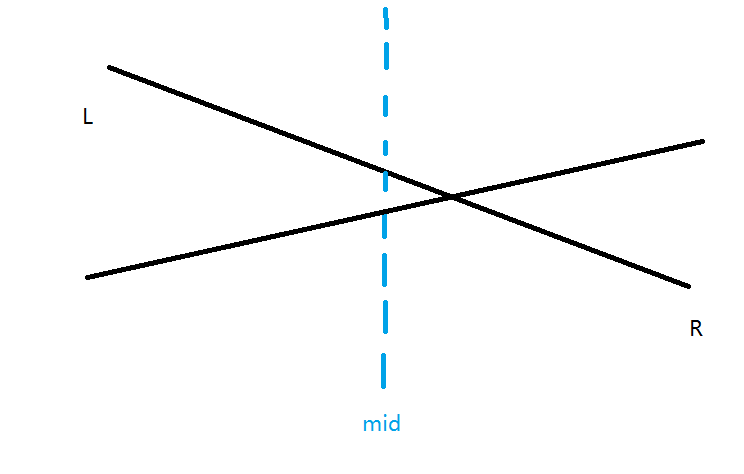
此时我们可以比较两个直线在 \(mid\) 上的取值,并将在 \(mid\) 上取值较大的直线 \(A\) 放在当前节点,然后考虑两条直线交点在 \(L\) 和 \(R\) 上的取值。
-
若 \(A_L>B_L\),则说明对于 \(mid\) 的左边部分,直线 \(A\) 的取值一定大于 \(B\),而对于 \(mid\) 的右边部分,两条直线取值的大小关系是不确定的。所以我们可以将 \(B\) 下放到右儿子进行递归加入;同理,若 \(A_L<B_L\),则将 \(B\) 下放到左儿子进行递归加入。
-
对于横坐标 \(x_k\) 最大值的查询,我们只需要查询所有包含 \(x_k\) 的节点直线在 \(x=x_k\) 时的取值,并取最大值作为答案即可。
这样做的正确性是显然正确的。
类似于这种修改时将贡献挂在节点上,查询时需要综合根到叶子节点上所有节点的答案的线段树,就叫线段树的标记永久化。注意到每一次修改时,我们最多只会选择左右子树中的一个进行下传;查询时,我们也只会查询从根到该叶子节点之间的所有节点。故总复杂度就是 \(O(n\log m)\) 的,其中 \(m\) 为直线的定义域大小。
Extension
插入线段
插入直线时,我们其实就相当于是在根节点上插入了一条定义域为 \([1,m]\) 的线段,所以插入一条线段其实就是将这个线段拆分成若干个线段树上的整区间之后,将这些区间作为根节点进行加入。
一条线段最多被拆分成 \(O(\log m)\) 个线段,每一条线段插入的复杂度都是 \(O(\log m)\) 的,所以总时间复杂度为 \(O(n \log^2m)\)。
struct node1{
double k,b;
int id;
node1 (double k=0,double b=0,int id=0)
:k(k),b(b),id(id){}
};
struct node{
double k[N<<2],b[N<<2];
int cnt,id[N<<2];
void add2(int i,int l,int r,double a,double c,int d){
if (!id[i]){
id[i]=d,k[i]=a,b[i]=c;
return;
}
int mid=l+r>>1;
double x=k[i]*mid+b[i],y=a*mid+c;
if (y>x) swap(k[i],a),swap(b[i],c),swap(id[i],d);
if (l==r) return;
if (k[i]==a) return;
x=k[i]*l+b[i],y=a*l+c;
if (y>x) add2(i<<1,l,mid,a,c,d);
else if (x>y) add2(i<<1|1,mid+1,r,a,c,d);
}
void add(int i,int l,int r,int ql,int qr,double a,double b,int c){
if (ql<=l&&r<=qr){
add2(i,l,r,a,b,c);
return;
}
int mid=l+r>>1;
if (ql<=mid) add(i<<1,l,mid,ql,qr,a,b,c);
if (mid<qr) add(i<<1|1,mid+1,r,ql,qr,a,b,c);
}
node1 query(int i,int l,int r,double x){
if (l==r){
return node1(k[i],b[i],id[i]);
}
node1 s;
int mid=l+r>>1;
if (x<=mid) s=query(i<<1,l,mid,x);
else s=query(i<<1|1,mid+1,r,x);
if (id[i]&&(!s.id||(k[i]*x+b[i]>s.k*x+s.b+eps||abs(k[i]*x+b[i]-s.k*x-s.b)<=eps&&id[i]<s.id))) s=node1(k[i],b[i],id[i]);
return s;
}
}S;
动态开点
类比普通线段树,对于定义域过大的情况,李超线段树也可以动态开点。
且由于李超线段树插入时的特殊性质,动态开点后的空间复杂度甚至是 \(O(n)\) 的 qwq.
删除线段
观察李超线段树的算法流程,可以很轻易地发现它是不支持删除线段的。
那么如果我们需要删除线段,该怎么做呢?
首先李超线段树虽然不支持删除,但是它显然是支持撤销的。所以若题目不强制在线,我们可以考虑使用线段树分治将所有操作离线来做。
于是考虑将所有的线段按照“存在时间”放到时间线段树上,到达一个节点就将这个节点的所有线段加入李超线段树,离开时撤销,遍历一遍整棵线段树即可。
结合 dp
单这样看,李超线段树好像并没有什么用,谁会出一道插入线段查询最值的题呢?
但是 OI 是充满变化的,而数据结构本身也只是起到一种辅助优化的作用。我们可以想一下,什么地方需要用到插入线段查询最值呢?
答案是斜率优化 dp。在斜率优化 dp 可以做的题目中,每一个决策事实上就是一条直线,而每一次转移其实就是在查询某一 \(x\) 坐标上的最值。单调队列优化只能处理查询坐标单调的情况,而对于查询坐标不单调的情况,我们显然是不能使用单调队列进行优化的。这时就可以用到我们的李超线段树进行优化转移。
其他
除此之外,类似于普通线段树,李超线段树还可以进行可持久化以及线段树合并的操作。
Problem
1. P4655 [CEOI2017] Building Bridges
普通的 dp 状态显然是很好设的,不妨设 \(dp_i\) 表示当前建桥建到了第 \(i\) 根柱子,且第 \(i\) 根柱子不拆的最小代价,\(s_i\) 表示拆除前 \(i\) 个柱子的价值,这有状态转移方程:
这式子一看就很斜率优化,于是可以考虑往这边想。
整理一下决策 \(j\) 的和 \(j\) 相关的贡献:
斜率好像并不单调?先向下推吧。
考虑对于当前状态 \(i\) 的两个决策 \(j,k\),其中 \(j<k\),当 \(j\) 可以取代 \(k\) 的时候,有:
也就是:
我们惊奇的发现 \(h_j-h_k\) 的正负我们都不知道,就算移项我们都不知道该怎么改变符号。
看来正常的斜率优化是行不通了,甚至我们没办法用二分单调队列的方式优化。
于是就祭出来我们的杀器——李超线段树。
观察发现,无论斜率单调不单调,也无论我们当前状态所表示的 \(x\) 值单调不单调,本质其实就只有两个操作:
- 插入一条直线 \(y=kx+b\)。
- 查询当 \(x=x_k\) 时 \(y\) 的最值。
这两个操作显然是可以用李超线段树解决的。于是我们转移时作一个查询,转移后作一个插入即可。
注意线段树维护的是值域,必要时可以动态开点。
2. CF932F Escape Through Leaf
由于要处理每一个节点的答案,所以显然可以想到树形 dp。
正着做不好做,可以考虑将题目反过来做,将【每个节点到达叶子节点费用的最小值】转化为【从叶子节点跳到第 \(i\) 个节点费用的最小值】。
设 \(dp_u\) 表示跳到节点 \(u\) 费用的最小值,则显然有转移方程:
这个形式十分斜率优化,但是 \(a,b\) 都不单调,所以考虑使用李超线段树辅助转移。又由于涉及到树上问题,需要将子树的信息合并给根节点,所以使用李超线段树合并即可。
李超线段树的合并与普通线段树类似,但并不相同。普通线段树合并只需要将两者公共部分合并,单独部分返回即可,单次合并时间复杂度为 \(O(size_{重叠部分})\)。但是李超线段树由于使用了标记永久化的缘故,显然不能这样合并。于是考虑一种比较暴力的合并方式:将一棵李超线段树上的线段从其原本所在深度暴力加入到另一棵上。
复杂度好像不对吧?
其实是对的。考虑每添加一条线段到一棵李超线段树上时,每判断两条线段之间的优劣,都会将一条线段的深度增加 \(1\),而总共只有 \(n\) 条线段,且每条线段的深度最多也就是 \(O(\log V)\),所以 \(n\) 条线段的深度之和最多是 \(O(n\log V)\),也就是最多将线段下放 \(O(n\log V)\) 次,复杂度自然也就是 \(O(n\log V)\)。
于是我们便证完了李超线段树合并的时间复杂度,这道题便做完了。
记得动态开点(废话
struct node1{
ll k[N],b[N],lson[N],rson[N];
int newnode(){
if (!htot) return ++cnt;
return hs[htot--];
}
int add(int o,int l,int r,ll a,ll c){
if (!o){
o=newnode();
k[o]=a,b[o]=c;
return o;
}
int mid=l+r>>1;
ll x=k[o]*(mid-M)+b[o],y=a*(mid-M)+c;
if (x>y) swap(k[o],a),swap(b[o],c);
if (l==r) return o;
x=k[o]*(l-M)+b[o],y=a*(l-M)+c;
if (x>y) lson[o]=add(lson[o],l,mid,a,c);
else if (x<y) rson[o]=add(rson[o],mid+1,r,a,c);
return o;
}
void pop(int x){
k[x]=b[x]=lson[x]=rson[x]=0;
hs[++htot]=x;
}
int merge(int l,int r,int o,int oo){
if (!oo) return o;
if (!o){
o=newnode();
k[o]=k[oo],b[o]=b[oo],lson[o]=lson[oo],rson[o]=rson[oo];
pop(oo);
return o;
}
if (l!=r){
int mid=l+r>>1;
lson[o]=merge(l,mid,lson[o],lson[oo]);
rson[o]=merge(mid+1,r,rson[o],rson[oo]);
}
o=add(o,l,r,k[oo],b[oo]);
pop(oo);
return o;
}
ll query(int o,int l,int r,int x){
if (!o) return INF;
int mid=l+r>>1;
ll ans=k[o]*(x-M)+b[o];
if (x<=mid) ans=min(query(lson[o],l,mid,x),ans);
else ans=min(query(rson[o],mid+1,r,x),ans);
return ans;
}
}S;
void dfs(int u,int fa){
bool flag=0;
for (int i=B.head[u];i;i=B.next[i]){
int v=B.to[i];
if (v!=fa){
flag=1;
dfs(v,u);
// cout<<gen[u]<<" "<<gen[v]<<" "<<u<<" "<<v<<"\n";
gen[u]=S.merge(0,M*2,gen[u],gen[v]);
}
}
if (flag) ans[u]=S.query(gen[u],0,M*2,s[u]+M);
gen[u]=S.add(gen[u],0,M*2,t[u],ans[u]);
}
Exercise
[JSOI2008]Blue Mary开公司 维护直线板子题
P4097 - [HEOI2013]Segment 维护线段板子题
CF1175G Yet Another Partiton Problem 思维难度颇高,有空填坑


 浙公网安备 33010602011771号
浙公网安备 33010602011771号