分块相关题目选做(一)
Idea
分块是根号算法的一个庞大分支。
本篇主要来记录一些分块的经典题目以及解法。
Problem
1. P2801 教主的魔法
区间加,查询区间大于等于 \(k\) 的数的个数。
考虑分块,对于每一个整块开一个 vector 记录本块的有序化数组。
设块大小为 \(m\).
-
区间加
我们将整块打一个 tag 标记,暴力修改散块元素的值并重构其所在块的有序数组。
时间复杂度 \(O(\frac{n}{m}+m\log m)\).
-
区间查询
对于每一个整块,我们在 vector 中二分查找 \(k\) 的位置,得到整块中大于等于 \(k\) 的元素个数;对于散块,我们暴力查找。
时间复杂度 \(O(\frac{n}{m}\log m+m)\)
我们取 \(m=\sqrt{n\log n}\) 即可得到最优复杂度 \(O(q\sqrt{n\log n})\).
2. P5356 [Ynoi2017] 由乃打扑克
区间加,查询区间第 \(k\) 小。
和上一题相比,查询由区间元素排名变成了区间第 \(k\) 小,本质上是将问题增强了的。
为什么增强了呢?因为区间 \(k\) 小是需要通过二分转化为求区间元素排名的,所以我们再上一题的基础上,还需要套一层二分答案。
但是这样还不够,因为这是 Ynoi,我们需要使用一些分块卡常技巧。
-
区间加
对于整块的区间加复杂度显然是很优的,但是对于散块的重构复杂度有些高。注意到如果我们将散块按照本次是否修改分成两部分,那么这两部分内部都是有序的。所以我们使用两个数组记录一下这两个部分,对于这两个数组归并即可。
-
区间查询
整块的区间查询好像也没办法作什么优化了,而对于散块里的每个元素,我们却都需要作 \(O(\log w)\) 的查询,这显然是不优的。考虑通过类似的归并将两个散块也临时合成一个整块,那么对于每一整个散块,我们都只需要二分查找 \(O(\log n)\) 次,优化了许多。
-
二分可行性判断1
找到询问区间的最值是容易的,所以我们可以再询问之前先查询询问区间的最值,缩小二分答案的上下界。
-
二分可行性判断2
由于数据的局限性,所以我们可以在二分到一个答案 \(mid\) 的时候,先判断当前块中的最大值是否小于等于 \(mid\),以及最小值是否大于 \(mid\),若是则直接返回块长或 \(0\)。如果不刻意卡的话,这个优化幅度是显著的。
除此之外,块长好像也是个玄学。分析出来的块长并不一定是最优的,直观感受是,我们对于整块的处理好像更多,所以块长应该略大于 \(O(\sqrt{n})\)。这里经测试采取的是 \(1000\) 的块长。
这些优化全加上,基本就过了。
其中优化 \(1\) 是普适的,\(2,3,4\) 都是由于本题二分答案的特点进行的优化。
第一道 Ynoi,调出来后世界都明朗了。
3. Chef and Churu
给长为 \(n\) 的序列,给定 \(n\) 个函数,每个函数为序列中第 \(l_i\) 到第 \(r_i\) 个数的和。
需要支持修改一个数的值,以及查询一段连续的函数值之和。
log 数据结构显然是不好维护的,于是考虑分块。
对于每次查询,我们显然会将所查询的函数区间分成整块和散块,整块由于 lazytag 的缘故,是好维护的,只需要对于每一个函数块记录一下每一个值在函数块内的出现次数以及该块的答案,单点修改时,对于每一个整块修改答案即可。
那么散块该怎么做呢?对于散块里的每一个函数,我们显然是希望做到 \(O(1)\) 查询单点值的,根据根号平衡,对于前者,我们需要设计一个 \(O(\sqrt n)\) 修改,\(O(1)\) 查询的算法,这显然是平凡的——我们只需要对于原序列的前缀和进行一个分块,就变成了根号平衡的一个经典例题(可能也叫块状数组罢)。
于是本题就解决了。对于整块内各个元素出现次数的记录可能需要树状数组的介入,所以整块的处理复杂度会变高,需要适当调大块长。
4. Loj6546.简单的数列题
考虑分块正常维护要求询问的答案。
对于区间加,散块随便维护,而对于整块的贡献则有些麻烦,因为由于 \(b\) 数组的存在,操作每一个位置的贡献是不同的,不太好打 tag。但是考虑将块内的元素放到图像上,那么其实块内的每一个元素都是一个一次函数。我们要做的其实就是找到块内图像的一个上凸壳。于是对于整块将当前 \(x\) 坐标右移,对于散块暴力重构凸壳即可。
对于交换操作,直接重构两个块的凸壳即可。
以及块长确实玄学(,感性分析就是,散块时间复杂度带 log(重构时将函数按照斜率排序),整块时间复杂度不带,所以需要让块长较 \(O(\sqrt{n})\) 偏小。这里个人取得块长是 \(100\)。
5. P4135 作诗
区间查询出现正偶数次元素个数,强制在线。
离线的话显然莫队随便做,在线就考虑分块了。
查询时还是要整块散块拆开查,所以我们也来分开讨论。一个自然的想法是快速处理出当前询问区间内所有整块中的答案,再动态加入散块元素并动态统计即可。
而对于每一个整块区间 \(k_{[i,j]}\) 答案的预处理,显然是 \(O(\frac{n^2}{b})\) 的,其中 \(b\) 为块长。除此之外,计算贡献的时候还需要判断在整块中元素的出现次数,这个也是可以通过前缀和预处理出来的。
最后取 \(b=\sqrt{n}\) 即可。
注意到我们本题分块算法的本质其实还是增量动态统计,与莫队本质相同。
启发式地来讲,静态分块的本质一般都与莫队相同。
6. P4168 [Violet]蒲公英
区间查询众数,强制在线。
如果莫队做的话就是回滚莫队了,但是要求强制在线,和上题一样,考虑与莫队本质相同的静态分块。
仿照上题,先预处理出每一个值在整块中出现次数的前缀和,再预处理出每一个块区间的答案,询问时先查询整块,再动态更新散块即可。
取块长 \(O(\sqrt{n})\),时间复杂度 \(O(n\sqrt{n})\).
7. P5048 [Ynoi2019 模拟赛] Yuno loves sqrt technology III
与上一题的区别是,本题要求空间 \(O(n)\).
观察上一题所开的数组,发现只有一个数组的空间是 \(O(n\sqrt{n})\) 的,那就是记录每个元素在前缀块内出现次数的数组。
这个数组的用途是什么呢?判断散块中的元素出现次数加上整块的出现次数后是否可以更新答案。所以我们需要考虑一种更节省空间的方式来判断散块元素是否可以更新答案。
考虑对于每个元素使用一个 vector 来记录该元素在数组中出现的位置,查询时设当前答案为 \(k\),我们可以一一枚举散块中的元素。若当前元素在左散块中最靠左出现,且在 vector 中下标加上 \(k\) 后依然没有超出查询区间的右端点,那么显然该元素的出现次数是大于 \(k\) 的,我们就可以更新的当前答案为 \(k+1\),右散块则反之。
由于散块中的元素一共只有 \(O(\sqrt{n})\) 个,所以我们显然最多也只会更新 \(O(\sqrt{n})\) 次答案,时间复杂度是正确的。
8. P3396 哈希冲突
根号分治。
考虑取模的特点: 对于大于 \(\sqrt{n}\) 的模数,具有相同余数的数最多只有 \(\sqrt{n}\) 个;而小于 \(\sqrt{n}\) 的模数则一共只有 \(\sqrt{n}\) 个。考虑从这里下手平衡复杂度。
一个很朴素的想法是,对于大于 \(\sqrt{n}\) 的模数,每次询问我们枚举 \(O(\sqrt{n})\) 个位置上值的总和即可;对于小于 \(\sqrt{n}\) 的模数,我们可以在每次修改之后暴力修改对于这些模数答案的贡献,查询时直接查询即可。
这道题的启发性是,取模可能和根号有关。
9. P5309 [Ynoi2011] 初始化
修改操作和上题差不多,考虑根号分治。
对于区间加操作,其实就是将所有下标取模 \(x\) 为 \(y\) 的星星亮度加 \(z\)。
考虑按照 \(x\) 的规模分治,若 \(x>\sqrt{n}\),则显然只会修改 \(O(\sqrt{n})\) 个数,而当 \(x<\sqrt{n}\) 时,则最多只有 \(O(\sqrt{n})\) 个模数。
对于前者,考虑根号平衡,对于每个数使用分块 \(O(1)\) 修改 \(O(\sqrt{n})\) 查询。
对于后者,则直接将加数挂在模数上,询问时枚举每一个模数,可以想到每一个模数其实就是将原序列分成了以该模数为块长的若干块,那么询问区间就相当于是包含了若干个整块和两边都散块。对于整块我们直接计算数量,加上这么多整块贡献即可;对于散块,其实就是一个后缀和一个前缀,所以我们在挂模数的时候顺带更新一下该模数的前缀后缀和即可。
总时间复杂度为 \(O(q\sqrt{n})\).
关于卡常:
- 注意到处理较小规模模数答案的时候常数更大,所以不妨将规模划分界限降低。
- 对于加法的取模可以采取手动取模的方式。
- long long 能不加就不加。
10. CF1580C Train Maintenance
由于我们查询的只有维修的数量,所以我们不妨将每一种列车对于答案的贡献差分,每 \(x_i+y_i\) 天当中的第 \(x_i+1\) 天加 \(1\),第 \(x_i+y_i+1\) 天减 \(1\)。
但这样复杂度显然是错的。感受到这熟悉的类似于【取模】的感觉,我们可以考虑根号分治。对于 \(x_i+y_i>\sqrt{n}\) 的列车,我们是只需要更新 \(O(\sqrt{n})\) 次的,复杂度正确;那么较小的该如何做呢?其实也和上题类似,本题修改的本质还是在一个模数的下修改一个余数的值,所以用一个数组记录修改即可。
查询时累计差分数组贡献,结合规模较小问题的答案,时间复杂度 \(O(n\sqrt{n})\).
实现时有一些细节需要考虑。
11. P3591 [POI2015] ODW
首先很容易想到当 \(k>\sqrt{n}\) 的时候,暴力倍增即可,时间复杂度一定不会超过 \(O(\sqrt{n})\)。
问题在于 \(k\le \sqrt{n}\) 的时候该怎么做。其实仔细思考一下就会发现,之前题目中对于规模较小问题的处理其实就类似于对于询问的一种预处理,我们只是在具体询问的时候查了一下预处理的表而已。
本题也一样,只不过我们的【修改】其实就是每一个节点的初始点权,所以对于小规模问题答案的处理更多算是预处理。预处理时对于每一个节点,不妨向上枚举 \(\sqrt{n}\) 个点,将小规模步伐的答案从上面继承下来。查询时作一个差分即可。
12. CF1039D You Are Given a Tree
如果不是询问 \([1,n]\) 中的每一个 \(k\),而是只询问一个 \(k\),那么便是一个经典的 树形dp/贪心 问题。
而现在询问的是每一个 \(k\),所以不妨按照 \(k\) 的规模分类讨论,对于 \(k\le \sqrt{n}\) 的情况,由于一共只有 \(\sqrt{n}\) 个 \(k\),所以对于每一个 \(k\) 作一遍贪心即可。那么当 \(k>\sqrt{n}\) 的时候呢?
此时显然答案最多只有 \(\sqrt{n}\) 条,也显然最多只有 \(\sqrt{n}\) 种答案,且当答案的条数单调上升的时候,相应的 \(k\) 一定是单调下降的——单调性?二分。
不妨枚举每一种答案,向后二分找到当前答案覆盖的区间,时间复杂度 \(O(n\sqrt{n}\log n)\)。
但是这个复杂度显然是不优秀的,因为我们发现我们对于大块处理的时间复杂度远高于小块,还可以再平衡一下。
设分界点为 \(p\),则小块的时间复杂度为 \(O(pn)\),大块的时间复杂度为 \(O(\frac{n^2\log n}{p})\),令二者取等,得 \(p=\sqrt{n\log n}\)。
感觉这道题好妙啊,优化的本质是什么呢?大概类似于下图:
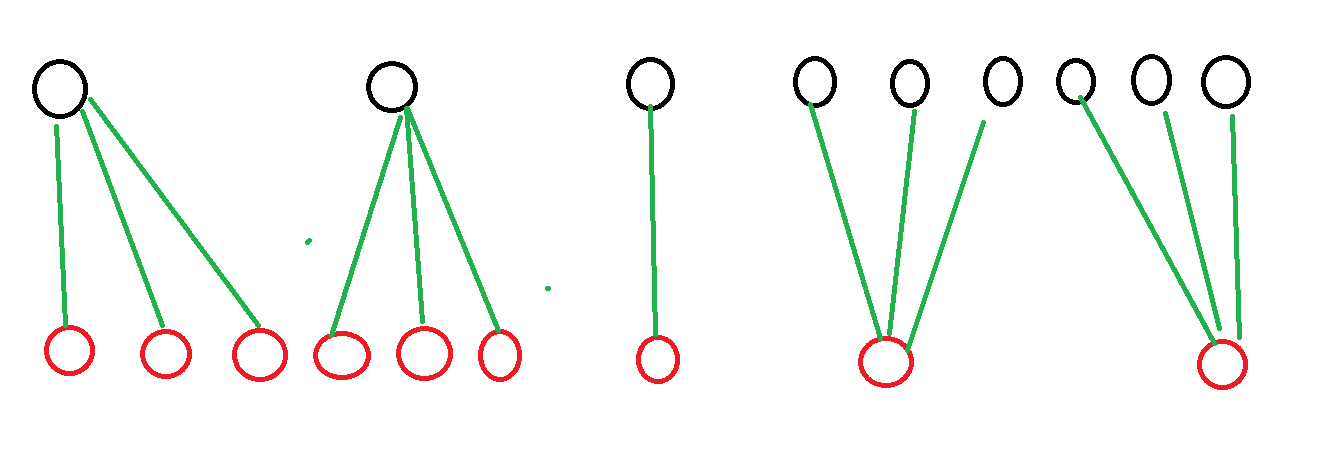
我们通过找到一个分界点,在黑点稀疏的时候枚举黑点,红点稀疏的时候枚举红点,由于黑点和红点的疏密程度是负相关的,时间复杂度就被优化了。而在这道题中,路径的长度 \(k\) 就是黑点,可以放置的路径个数就是红点。本质上来讲,其实就是因为两者的乘积上限为定值 \(n\),于是路径的长度与其最多能放置的路径个数构成了反比例函数关系。
除了根号分治的做法以外,本题还可以采用整体二分的方法,两者的优化本质其实是类似的。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号