二叉排序树

二叉排序树

什么是二叉排序树、

二叉排序树要么是空二叉树，要么具有如下性质：

二叉排序树中，如果其根结点有左子树，那么左子树上所有结点的值都小于根结点的值；
二叉排序树中，如果其根结点有右子树，那么右子树上所有结点的值都大于根结点的值；
二叉排序树的左右子树也要求都是二叉排序树.

例子

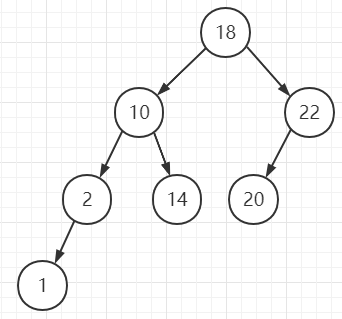
根据以上性质，我们得知二叉排序树的中序遍历是一个有序序列（升序），如上图中序遍历得到的序列为：1 2 10 14 18 20 22

结构定义

struct Node {
    int key;
    Node *lchild, *rchild;
};

节点初始化

我们定义一个函数Node* getNewNode(int key)，其传入参数是一个key，返回值为一个节点地址，表示初始化一个具体key值的节点，这里是为了给插入节点函数服务所实现的。

Node *getNewNode(int key) {
    Node *p = (Node *)malloc(sizeof(Node));
    p->key = key;
    p->lchild = p->rchild = NIL;
}

插入操作

根据上面二叉排序树的性质1和性质2，当我们往一个二叉排序树种插入一个节点时，当要插入的节点的key值小于根节点的key值，则递归插入到根节点的左子树；若要插入的节点的key值大于根节点的key值，则递归插入到根节点的右子树；若二叉排序树中存在与要插入节点一样key值得节点，则不插入并返回该节点的地址。由于性质决定，插入的新节点，一定会是二叉排序树的叶子节点。

代码

Node *insert(Node *root, int key) {
    //root是空，则表明从根节点遍历到这个空节点都没有找到与参数key值一样的节点，可以在这里插入新节点，且插入后该节点为叶子节点
    if (root == NULL) {
        return getNewNode(key);
    }
    if (key == root->key) {//这里不重复插入相同key值得节点
        return root;
    }
    if (key < root->key) {//若插入key比当前节点的key小，则递归到当前节点的左子树中去插入
        root->lchild = insert(root->lchild, key);
    } else (key > root->key) {//若插入key比当前节点的key大，则递归到当前节点的右子树中去插入
        root->rchild = insert(root->rchild, key);
    }
    return root;
}

删除操作

根据删除节点的度来区分，我们可以把删除操作主要分为三个部分，：

删除度为0的节点 -> 直接删除
删除度为1的节点 -> 把删除节点的孤儿节点挂到自己的位置上
删除度为2的节点 -> 转化为删除要删除节点的前驱或者后继

对于度为2的节点：
前驱 -> 左子树的最大值
后继 -> 右子树的最小值
删除度为2的例子
比如我们想删除节点23，节点23度为2，这时候我们找到它的前驱节点19，把前驱节点的key值填到23节点的位置，再删除23的前驱节点19。

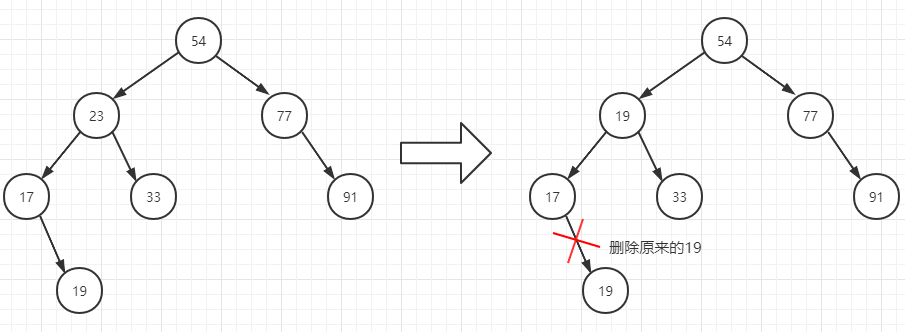
代码

求出某个节点前驱的代码

//传入某个节点的地址root，然后求出root节点的前驱节点的地址，并返回
Node *prodecessor(Node *root) {
    Node *p = root->lchild;
    while (p->rchild != NULL) {
        p = p->rchild;
    }
    return p;
}

删除节点代码

Node *erase(Node *root, int key) {
    //root是空，则表明从根节点遍历到这个空节点都没有找到与参数key值一样的节点,直接返回
    if (root == NULL) {
        return root;
    }
    if (key < root->key) {//key值小于当前节点的key，则要删除的点在root的左子树上
        root->lchild = erase(root->lchild, key);
    } else if (key > root->key) {//key值大于当前节点的key，则要删除的点在root的左子树上
        root->rchild = erase(root->rchild, key);
    } else {//key值与当前节点的key一样，则以度的数量开始区分删除情况。
        if (root->lchild == NULL && root->rchild == NULL) {//度为0：直接删除
            free(root);;
            return NULL;
        } else if (root->lchild == NULL || root->rchild == NULL) {//度为1：直接返回孤儿节点的地址给自身
            Node *temp = root->lchild == NULL ? root->rchild : root->lchild;
            free(root);
            return temp;
        } else {//度为2：直接转化为删除该节点的前驱节点
            Node *temp = predecessor(root);
            root->key = temp->key;
            root->lchild = erase(root->lchild, temp->key);
        }
    }
    return root;
}

遍历二叉排序树

这里我们采用中序遍历的方式遍历二叉排序树。

void in_order(Node *root) {
    if (root == NULL) {
        return ;
    }
    in_order(root->lchild);
    printf("%d ", root->key);
    in_order(root->rchild);
    return ;
}

完整代码

这里我们给出完整代码，该代码带有测试程序，首先根据提示，有选择操作的选项，输入1表示插入操作；输入2表示删除操作，选择完操作后，需要输入一个key，然后每次操作完毕，都会中序遍历输出该二叉排序树的所有节点。

#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>

#define KEY(n) (n ? n->key : -1)

typedef struct Node {
    int key;
    struct Node *lchild, *rchild;
} Node;

Node *getNewNode(int key) {
    Node *p = (Node *)malloc(sizeof(Node));
    p->key = key;
    p->lchild = p->rchild = NULL;
}

void clear(Node *root) {
    if (root == NULL) {
        return ;
    }
    clear(root->lchild);
    clear(root->rchild);
    free(root);
    return ;
}

Node *insert(Node *root, int key) {
    //root是空，则表明从根节点遍历到这个空节点都没有找到与参数key值一样的节点，可以在这里插入新节点，且插入后该节点为叶子节点
    if (root == NULL) {
        return getNewNode(key);
    }
    if (root->key == key) {//这里不重复插入相同key值得节点
        return root;
    }
    if (key < root->key) {//若插入key比当前节点的key小，则递归到当前节点的左子树中去插入
        root->lchild = insert(root->lchild, key);
    } else {//若插入key比当前节点的key大，则递归到当前节点的右子树中去插入
        root->rchild = insert(root->rchild, key);
    }
    return root;
}


Node *prodecessor(Node *root) {
    Node *p = root->lchild;
    while (p->rchild != NULL) {
        p = p->rchild;
    }
    return p;
}

Node *erase(Node *root, int key) {
    //root是空，则表明从根节点遍历到这个空节点都没有找到与参数key值一样的节点,直接返回
    if (root == NULL) {
        return root;
    }
    if (key < root->key) {//key值小于当前节点的key，则要删除的点在root的左子树上
        root->lchild = erase(root->lchild, key);
    } else if (key > root->key){//key值大于当前节点的key，则要删除的点在root的左子树上
        root->rchild = erase(root->rchild, key);
    } else {//key值与当前节点的key一样，则以度的数量开始区分删除情况。
        if (root->lchild == NULL && root->rchild == NULL) {//度为0：直接删除
            free(root);
            return NULL;
        } else if (root->lchild == NULL || root->rchild == NULL) {//度为1：直接返回孤儿节点的地址给自身
            Node *p = root->lchild == NULL ? root->rchild : root->lchild;
            free(root);
            return p;
        } else {//度为2：直接转化为删除该节点的前驱节点
            Node *p = prodecessor(root);
            root->key = p->key;
            root->lchild = erase(root->lchild, p->key);
        }
    }
    return root;
}

void print_node(Node *root) {
    printf("(%d: %d, %d)\n", KEY(root), KEY(root->lchild), KEY(root->rchild));
}

void _in_order(Node *root) {
    if (root == NULL) {
        return ;
    }
    _in_order(root->lchild);
    print_node(root);
    _in_order(root->rchild);
    return ;
}

void in_order(Node *root) {
    printf("binary tree:\n");
    _in_order(root);
    printf("\n\n");
}

void menu(void) {
    printf("Please enter the operation: \n");
    printf("Press 1 to insert a node to binary search tree\n");
    printf("Press 2 to delete a node from binary search tree\n");
    printf("Press TRL + D to quit!\n");
}

int main() {
    Node *root = NULL;
    int op, key;
    menu();
    while (~scanf("%d", &op)) {
        if (op != 1 && op != 2) {
            printf("please enter the right operation!\n");
            continue;
        }
        switch (op) {
            case 1:
                printf("Enter the key you want to insert: ");
                scanf("%d", &key);
                root = insert(root, key);
            break;

            case 2:
                printf("Enter the key you want to delete: ");
                scanf("%d", &key);
                root = erase(root, key);
            break;
        }
        in_order(root);
        menu();
    }
    clear(root);
    return 0;
}

测试结果

Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press TRL + D to quit!
1
Enter the key you want to insert: 12
binary tree:
(12: -1, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press TRL + D to quit!
1
Enter the key you want to insert: 8
binary tree:
(8: -1, -1)
(12: 8, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press TRL + D to quit!
1
Enter the key you want to insert: 34
binary tree:
(8: -1, -1)
(12: 8, 34)
(34: -1, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press TRL + D to quit!
1
Enter the key you want to insert: 56
binary tree:
(8: -1, -1)
(12: 8, 34)
(34: -1, 56)
(56: -1, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press TRL + D to quit!
2 12
Enter the key you want to delete: binary tree:
(8: -1, 34)
(34: -1, 56)
(56: -1, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press TRL + D to quit!
1 12
Enter the key you want to insert: binary tree:
(8: -1, 34)
(12: -1, -1)
(34: 12, 56)
(56: -1, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press TRL + D to quit!

思考

如果我们分别进行两棵二叉排序树的插入构建。其中插入到这两棵树的节点的key和节点数量完全相同，唯一不同的是插入顺序不同，例如：
第一棵树按一下顺序插入6个元素： 6 9 3 2 7 5
第二棵树按以下顺序插入6个元素： 2 3 5 6 7 9
查找一个元素的时间复杂度一样吗？
这里，我们先直接画出这两棵树
第一棵

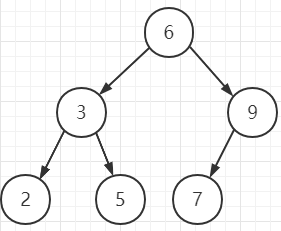
第二棵

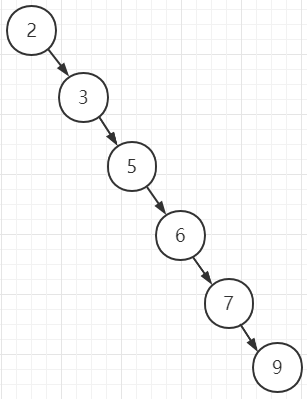
这里的时候，第一棵二叉排序树的元素平均查找期望是(1+2*2+3*3)/6 = 5/2，大致是O(logN)级别的时间复杂度；而第二棵树的凭据查找期望是(1+2+3+4+5+6)/6 = 7/3，且这很明显，这里第二颗树已经退化成链表，这时候它的查找效率是O(N)，而对比第一棵树，由于是一棵完全二叉树，其查找效率在O(logN)。由此，我们可以下定结论：

1. 插入顺序会影响最终的树形结构
2. 不同的树形结构，查找效率不同

为了解决以上二叉排序树会退化成链表，导致查找效率变低的情况，在二叉排序树的基础上，二叉平衡树诞生了。

拓展

二叉排序树的删除代码优化

删除掉处理度为0的代码逻辑，不影响代码整体功能

Node *erase(Node *root, int key) {
    //root是空，则表明从根节点遍历到这个空节点都没有找到与参数key值一样的节点,直接返回
    if (root == NULL) {
        return root;
    }
    if (key < root->key) {//key值小于当前节点的key，则要删除的点在root的左子树上
        root->lchild = erase(root->lchild, key);
    } else if (key > root->key) {//key值大于当前节点的key，则要删除的点在root的左子树上
        root->rchild = erase(root->rchild, key);
    } else {//key值与当前节点的key一样，则以度的数量开始区分删除情况。
        if (root->lchild == NULL || root->rchild == NULL) {//删除度为0或者1都可以这个分支。
            Node *temp = root->lchild == NULL ? root->rchild : root->lchild;
            delete root;
            return temp;
        } else {//度为2：直接转化为删除该节点的前驱节点
            Node *temp = predecessor(root);
            root->key = temp->key;
            root->lchild = erase(root->lchild, temp->key);
        }
    }
    return root;
}

如何解决排名相关的检索需求

1. 修改二叉排序树的结构定义，增加 size 字段，记录每棵树的节点数量
2. 若K = LS + 1，则根节点就是排名第 k 位的元素
3. 若K <= LS，则排名第 K 位的元素在左子树中
4. 若K > LS + 1，则排名第 k 位的元素在右子树中
   PS：LS指某个节点的左子树节点数量

带排名版本的二叉排序树

结构定义

typedef struct Node {
    int key, size;
    struct Node *lchild, *rchild;
} Node;

在结构定义中，增加了size字段名，用来记录每个子树的节点数量。

节点初始化

Node *getNewNode(int key) {
    Node *p = (Node *)malloc(sizeof(Node));
    p->key = key;
    p->size = 1;
    p->lchild = p->rchild = NULL;
}

节点初始化，由于增加了size字段，同样的，节点初始化的时候，size字段也要初始化为1.

子树节点数量更新函数

void update_size(Node *root) {
    root->size = SIZE(root->lchild) + SIZE(root->rchild) + 1;
}

每一个根节点的节点数量为其左右子树节点数的和加1。

插入

Node *insert(Node *root, int key) {
    //root是空，则表明从根节点遍历到这个空节点都没有找到与参数key值一样的节点，可以在这里插入新节点，且插入后该节点为叶子节点
    if (root == NULL) {
        return getNewNode(key);
    }
    if (root->key == key) {//这里不重复插入相同key值得节点
        return root;
    }
    if (key < root->key) {//若插入key比当前节点的key小，则递归到当前节点的左子树中去插入
        root->lchild = insert(root->lchild, key);
    } else {//若插入key比当前节点的key大，则递归到当前节点的右子树中去插入
        root->rchild = insert(root->rchild, key);
    }
    update_size(root);//更新节点数量
    return root;
}

在插入操作返回前，必须先更新节点数量。

删除

Node *erase(Node *root, int key) {
    //root是空，则表明从根节点遍历到这个空节点都没有找到与参数key值一样的节点,直接返回
    if (root == NULL) {
        return root;
    }
    if (key < root->key) {//key值小于当前节点的key，则要删除的点在root的左子树上
        root->lchild = erase(root->lchild, key);
    } else if (key > root->key){//key值大于当前节点的key，则要删除的点在root的左子树上
        root->rchild = erase(root->rchild, key);
    } else {//key值与当前节点的key一样，则以度的数量开始区分删除情况。
        if (root->lchild == NULL || root->rchild == NULL) {//删除度为0或者1都可以这个分支。
            Node *p = root->lchild == NULL ? root->rchild : root->lchild;
            free(root);
            return p;
        } else {////度为2：直接转化为删除该节点的前驱节点
            Node *p = prodecessor(root);
            root->key = p->key;
            root->lchild = erase(root->lchild, p->key);
        }
    }
    update_size(root);//更新节点数量
    return root;
}

同样的，在删除操作返回前，也要更新节点数量。

注意：

无论是插入还是删除，之所以在返回root节点前更新节点数量，这是因为插入和删除只会影响到回溯时经过的节点（也就是插入节点的祖先节点）对应的子树的节点数量。

查找第K位元素

int find_k(Node *root, int k) {
    if (root == NULL || k == 0) {
        return -1;
    }
    if (k == SIZE(root->lchild) + 1) {//若root节点的左子树节点数量 + 1等于 k，则root节点就是第K个节点
        return root->key;
    }
    if (k <= SIZE(root->lchild)) {//若root节点的左子树节点数量大于等于k，则递归到左子树中去找第K个节点
        return find_k(root->lchild, k);
    }
    //若root左子树节点数量 + 1小于K，则递归到右子树中去找右子树中第K - size(L(root)) - 1个节点。
    if (k > SIZE(root->lchild) + 1) {
        return find_k(root->rchild, k - SIZE(root->lchild) - 1);
    }
}

宏定义

#define KEY(n) (n ? n->key : -1)//返回某个节点的key值
#define SIZE(n) (n ? n->size : 0)//返回某个节点对应的树的节点数量

解决 Top-K 问题（找到小于第 k 位的所有元素）

1. 根节点就是第 k 位元素的话，就把左子树中的值全部输出出来
2. 第 k 位在左子树中，前 k 位元素全都在左子树中
3. 第 k 位在右子树中，说明根节点和左子树中的元素，都是前 k 位元素里面的值

void output_k(Node *root, int k) {
    if (root == NULL || k <= 0) {
        return ;
    }
    if (k == SIZE(root->lchild)) {
        _in_order(root->lchild);
    } else if (k < SIZE(root->lchild)) {
        output_k(root->lchild, k);
    } else {
        _in_order(root->lchild);
        print_node(root);
        output_k(root->rchild, k - SIZE(root->lchild) - 1);
    }
}

加上拓展后的完整代码

#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>

#define KEY(n) (n ? n->key : -1)
#define SIZE(n) (n ? n->size : 0)

typedef struct Node {
    int key, size;
    struct Node *lchild, *rchild;
} Node;

Node *getNewNode(int key) {
    Node *p = (Node *)malloc(sizeof(Node));
    p->key = key;
    p->size = 1;
    p->lchild = p->rchild = NULL;
}

void clear(Node *root) {
    if (root == NULL) {
        return ;
    }
    clear(root->lchild);
    clear(root->rchild);
    free(root);
    return ;
}

void update_size(Node *root) {
    root->size = SIZE(root->lchild) + SIZE(root->rchild) + 1;
}

Node *insert(Node *root, int key) {
    //root是空，则表明从根节点遍历到这个空节点都没有找到与参数key值一样的节点，可以在这里插入新节点，且插入后该节点为叶子节点
    if (root == NULL) {
        return getNewNode(key);
    }
    if (root->key == key) {//这里不重复插入相同key值得节点
        return root;
    }
    if (key < root->key) {//若插入key比当前节点的key小，则递归到当前节点的左子树中去插入
        root->lchild = insert(root->lchild, key);
    } else {//若插入key比当前节点的key大，则递归到当前节点的右子树中去插入
        root->rchild = insert(root->rchild, key);
    }
    update_size(root);
    return root;
}

Node *prodecessor(Node *root) {
    Node *p = root->lchild;
    while (p->rchild != NULL) {
        p = p->rchild;
    }
    return p;
}

Node *erase(Node *root, int key) {
    //root是空，则表明从根节点遍历到这个空节点都没有找到与参数key值一样的节点,直接返回
    if (root == NULL) {
        return root;
    }
    if (key < root->key) {//key值小于当前节点的key，则要删除的点在root的左子树上
        root->lchild = erase(root->lchild, key);
    } else if (key > root->key){//key值大于当前节点的key，则要删除的点在root的左子树上
        root->rchild = erase(root->rchild, key);
    } else {//key值与当前节点的key一样，则以度的数量开始区分删除情况。
        if (root->lchild == NULL || root->rchild == NULL) {//删除度为0或者1都可以这个分支。
            Node *p = root->lchild == NULL ? root->rchild : root->lchild;
            free(root);
            return p;
        } else {////度为2：直接转化为删除该节点的前驱节点
            Node *p = prodecessor(root);
            root->key = p->key;
            root->lchild = erase(root->lchild, p->key);
        }
    }
    update_size(root);
    return root;
}

void print_node(Node *root) {
    printf("(%d[%d]: %d, %d)\n", KEY(root), SIZE(root), KEY(root->lchild), KEY(root->rchild));
}

void _in_order(Node *root) {
    if (root == NULL) {
        return ;
    }
    _in_order(root->lchild);
    print_node(root);
    _in_order(root->rchild);
    return ;
}

void in_order(Node *root) {
    printf("binary tree:\n");
    _in_order(root);
    printf("\n\n");
}

int find_k(Node *root, int k) {
    if (root == NULL || k == 0) {
        return -1;
    }
    if (k == SIZE(root->lchild) + 1) {//若root节点的左子树节点数量 + 1等于 k，则root节点就是第K个节点
        return root->key;
    }
    if (k <= SIZE(root->lchild)) {//若root节点的左子树节点数量大于等于k，则递归到左子树中去找第K个节点
        return find_k(root->lchild, k);
    }
    //若root左子树节点数量 + 1小于K，则递归到右子树中去找右子树中第K - size(L(root)) - 1个节点。
    if (k > SIZE(root->lchild) + 1) {
        return find_k(root->rchild, k - SIZE(root->lchild) - 1);
    }
}

void menu(void) {
    printf("Please enter the operation: \n");
    printf("Press 1 to insert a node to binary search tree\n");
    printf("Press 2 to delete a node from binary search tree\n");
    printf("Press 3 to find a node from binary search tree\n");
    printf("Press 4 to output top-k sequence from binary search tree\n");
    printf("Press TRL + D to quit!\n");
}

int main() {
    Node *root = NULL;
    int op, val;
    menu();
    while (~scanf("%d", &op)) {
        if (op < 1 || op > 4) {
            printf("please enter the right operation!\n");
            continue;
        }
        switch (op) {
            case 1:
                printf("Enter the key you want to insert: ");
                scanf("%d", &val);
                root = insert(root, val);
            break;

            case 2:
                printf("Enter the key you want to delete: ");
                scanf("%d", &val);
                root = erase(root, val);
            break;

            case 3:
                printf("Enter the index you are looking for:");
                scanf("%d", &val);
                printf("Find NO.%d of the binary tree, result: %d\n\n", val, find_k(root, val));
            break;

            case 4:
                printf("Enter a k for output top-k sequence: ");
                scanf("%d", &val);
                output_k(root, val);
                printf("\n");
            break;
        }
        if (op != 3 && op != 4) {
            in_order(root);
        }
        menu();
    }
    clear(root);
    return 0;
}

测试结果

Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!
1
Enter the key you want to insert: 12
binary tree:
(12[1]: -1, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!
1
Enter the key you want to insert: 8
binary tree:
(8[1]: -1, -1)
(12[2]: 8, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!
1
Enter the key you want to insert: 10
binary tree:
(8[2]: -1, 10)
(10[1]: -1, -1)
(12[3]: 8, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!
1
Enter the key you want to insert: 9
binary tree:
(8[3]: -1, 10)
(9[1]: -1, -1)
(10[2]: 9, -1)
(12[4]: 8, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!
1
Enter the key you want to insert: 34
binary tree:
(8[3]: -1, 10)
(9[1]: -1, -1)
(10[2]: 9, -1)
(12[5]: 8, 34)
(34[1]: -1, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!
1
Enter the key you want to insert: 23
binary tree:
(8[3]: -1, 10)
(9[1]: -1, -1)
(10[2]: 9, -1)
(12[6]: 8, 34)
(23[1]: -1, -1)
(34[2]: 23, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!
1
Enter the key you want to insert: 20
binary tree:
(8[3]: -1, 10)
(9[1]: -1, -1)
(10[2]: 9, -1)
(12[7]: 8, 34)
(20[1]: -1, -1)
(23[2]: 20, -1)
(34[3]: 23, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!
1
Enter the key you want to insert: 18
binary tree:
(8[3]: -1, 10)
(9[1]: -1, -1)
(10[2]: 9, -1)
(12[8]: 8, 34)
(18[1]: -1, -1)
(20[2]: 18, -1)
(23[3]: 20, -1)
(34[4]: 23, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!
1
Enter the key you want to insert: 17
binary tree:
(8[3]: -1, 10)
(9[1]: -1, -1)
(10[2]: 9, -1)
(12[9]: 8, 34)
(17[1]: -1, -1)
(18[2]: 17, -1)
(20[3]: 18, -1)
(23[4]: 20, -1)
(34[5]: 23, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!
1
Enter the key you want to insert: 19
binary tree:
(8[3]: -1, 10)
(9[1]: -1, -1)
(10[2]: 9, -1)
(12[10]: 8, 34)
(17[1]: -1, -1)
(18[3]: 17, 19)
(19[1]: -1, -1)
(20[4]: 18, -1)
(23[5]: 20, -1)
(34[6]: 23, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!
1
Enter the key you want to insert: 21
binary tree:
(8[3]: -1, 10)
(9[1]: -1, -1)
(10[2]: 9, -1)
(12[11]: 8, 34)
(17[1]: -1, -1)
(18[3]: 17, 19)
(19[1]: -1, -1)
(20[5]: 18, 21)
(21[1]: -1, -1)
(23[6]: 20, -1)
(34[7]: 23, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!
1
Enter the key you want to insert: 25
binary tree:
(8[3]: -1, 10)
(9[1]: -1, -1)
(10[2]: 9, -1)
(12[12]: 8, 34)
(17[1]: -1, -1)
(18[3]: 17, 19)
(19[1]: -1, -1)
(20[5]: 18, 21)
(21[1]: -1, -1)
(23[7]: 20, 25)
(25[1]: -1, -1)
(34[8]: 23, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!
1
Enter the key you want to insert: 28
binary tree:
(8[3]: -1, 10)
(9[1]: -1, -1)
(10[2]: 9, -1)
(12[13]: 8, 34)
(17[1]: -1, -1)
(18[3]: 17, 19)
(19[1]: -1, -1)
(20[5]: 18, 21)
(21[1]: -1, -1)
(23[8]: 20, 25)
(25[2]: -1, 28)
(28[1]: -1, -1)
(34[9]: 23, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!
2
Enter the key you want to delete: 17
binary tree:
(8[3]: -1, 10)
(9[1]: -1, -1)
(10[2]: 9, -1)
(12[12]: 8, 34)
(18[2]: -1, 19)
(19[1]: -1, -1)
(20[4]: 18, 21)
(21[1]: -1, -1)
(23[7]: 20, 25)
(25[2]: -1, 28)
(28[1]: -1, -1)
(34[8]: 23, -1)


Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!
3
Enter the index you are looking for:4
Find NO.4 of the binary tree, result: 12

Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!
3
Enter the index you are looking for:10
Find NO.10 of the binary tree, result: 25

Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!
4
Enter a k for output top-k sequence: 7
(8[3]: -1, 10)
(9[1]: -1, -1)
(10[2]: 9, -1)
(12[12]: 8, 34)
(18[2]: -1, 19)
(19[1]: -1, -1)
(20[4]: 18, 21)

Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!
4
Enter a k for output top-k sequence: 3
(8[3]: -1, 10)
(9[1]: -1, -1)
(10[2]: 9, -1)

Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!
4
Enter a k for output top-k sequence: 4
(8[3]: -1, 10)
(9[1]: -1, -1)
(10[2]: 9, -1)
(12[12]: 8, 34)

Please enter the operation:
Press 1 to insert a node to binary search tree
Press 2 to delete a node from binary search tree
Press 3 to find a node from binary search tree
Press 4 to output top-k sequence from binary search tree
Press TRL + D to quit!

原创博文，转发请加上原链接