线性表（2）-- 链表

导言

　　顺序表是有缺点的，其中最大的缺点就是插入和删除时需要移动大量元素，这显然很浪费时间，这时候需要找另一种逻辑结构的线性表来替换它。

1. 链表存储结构

　　线性表的链式存储结构的特点是用一组任意的存储单元存储线性表的数据元素，这组存储单元可以是连续的，也可以是不连续的。每个数据元素除了存储数据外，还需要存储一个指示其直接后继的信息（即直接后继的存储位置）。我们把存储数据元素信息的域称为数据域，把存储直接后继位置的域称为指针域。指针域中存储的信息称做指针或链。这两部分信息组成数据元素ai的存储映像，称为结点（Node）。

1.1 单链表

　　n个结点链构成一个链表，即为线性表的链式存储结构，因为连接的每个结点中只包含一个指针域，所以叫做单链表。

1.2 单链表存储结构代码描述

　　单链表中，我们在C语言中可用结构体来描述。

/*线性表的单链表存储结构*/
typedef struct Node{   
    int data;          
    struct Node *next; 
                       
}Node, *LinkList; 

　　我们定义的结点结构如上，其中data是一个整型的数据域，next是一个Node*指针域，它们合并在一个结构体里表示一个Node结点。

1.3 单链表的操作

　　我们约定，头结点的序号为0，且头结点的数据域是有效数据域。

　　常见的单链表操作有创建，插入，删除，遍历，查找，销毁等，这些操作都是单链表最基础的部分，有了这些基础的操作就可以实现其他的操作，比如更新一个结点的数据，我们可以通过key值（比如结点的位置）来查找到某个结点，再修改里面的数据。

1.3.1 单链表的创建

void InitList(LinkList *head){
    *head = NULL;
}

　　这里只是单纯为了好理解，我们封装了单链表的头结点初始化，表示最开始创建的单链表是一个空链表。需要注意的是，由于我们采用函数参数来充当返回值，并且返回的是一个头结点head，是一个LinkList，所以我们需要把head的地址当做参数，其类型也就是LinkList*。

1.3.2 单链表的插入

　　

/*
    参数：
        head  -- 头结点指针的地址
        node  -- 插入结点的地址
        index -- 结点要插入的位置
    描述：
        把一个结点node插入到单链表head的index个位置上。
    返回值：
        成功返回 OK，失败返回 ERROR。
*/
int ListInsert(LinkList *head, Node *node, int index){
    //如果链表为空，且要插入的位置是第0个节点
    if(*head == NULL){
        if(index != 0){
            return ERROR;
        }
        *head = node;
        return OK;
    }

    //如果链表不为空，且要插入的位置是第0个节点
    if(index == 0){
        node->next = *head;
        *head = node;
        return OK;
    }

    //如果链表不为空，且要插入的位置是非第0个结点
    Node *current_node = *head;
    int count = 0;
    while(current_node->next != NULL && count < index - 1){
        current_node = current_node->next;
        count++;
    }

    if(count == index - 1){
        node->next = current_node->next;
        current_node->next = node;
        return OK;
    }else{
        return ERROR;
    }
}

 　　首先，根据插入位置和是否是第一次插入，我们可以把单链表的插入情况分为有三种：

　　1）第一次插入且插入序号必须是为0；

　　2）非第一次插入且序号为0；

　　3）非第一次插入且序号不为0.

 　　首先，我们先来分析第一个情况，因为是第一次插入，所以链表本身就是空的，故插入的结点node就是相当于头结点，因为我们约定序号0就是头结点，所以如果插入的index是非0的值，我们返回ERROR，13~19行就是处理该情况的代码。我们可以结合图1-1来理解。

　

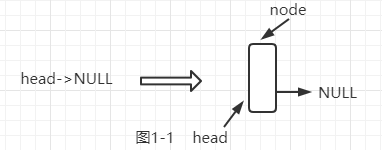
　　接下来我们来分析第二种情况，如果不是第一次插入，且插入的序号index是0，我们只需要让要插入的结点node的next指针指向头结点head，然后又移动head指针指向node结点，使node结点成为头结点。22~26行就是处理该情况的代码。我们可以配合图1-2来理解。

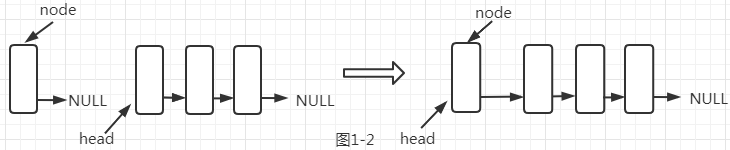
 　　接下来就分析第三中情况，非第一次插入且序号index不为0，这种情况是最复杂的情况，假设我们要插入的位置为index，这样的话我们必须找到index的上一个结点，即序号为index-1的结点，为了找到这个结点，我们必须遍历链表知道index-1，然后在index-1结点后面插入node结点。代码29~42行就是处理该情况下的逻辑。配合图1-3来理解。

　　时间复杂度分析，我们假设链表一共有n个结点，如果我们插入的是头结点，则我们不需要遍历链表，直接插入，则时间复杂度为1。若要插入的位置为index（0<=index<=n），则我们需要移动index-1。综上我们可以得到时间复杂度为：

 

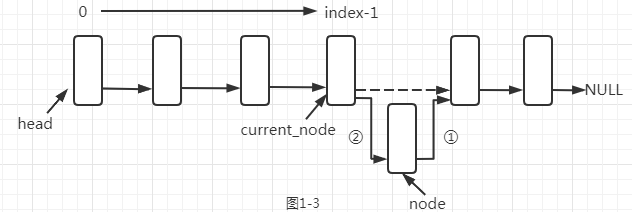
 　　结合图1-3，当我们定位到index-1后，进行插入操作，需要注意的是防止链表断连，所以我们要先让插入结点的node->next指针指向index-1结点的next，再把index-1结点的next指向node。

1.3.3 单链表的删除

/*
    参数：
        head  -- 头结点指针的地址
        index -- 要删除结点的序号
    描述：
        把序号为index的结点从链表head中删除
    返回值：
        成功返回 OK，失败返回 ERROR。
*/
int ListDelete(LinkList *head, int index){
    //如果链表为空，则返回
    if(*head == NULL){
        return ERROR;
    }

    //链表不为空，且删除的结点是第一个结点
    if(index == 0){
        Node *delete_node = *head;
        *head = (*head)->next;
        free(delete_node);
    }

    Node *current_node = *head;
    int count = 0;
    while(current_node->next != NULL && count < index-1){
        current_node = current_node->next;
        count++;
    }

    if(count == index-1){
        Node *delete_node = current_node->next;
        current_node->next = delete_node->next;
        free(delete_node);
        return OK;
    }else{
        return ERROR;
    }

}

　　首先，链表的删除分为两种情况，

　　1）删除的结点是头结点；

　　2）删除的结点是非头结点。

　　如果是第一种情况，我们只需要把head的指针备份一份，再把head指向head的后继，即head = head->next。如下图1-4所示。

　

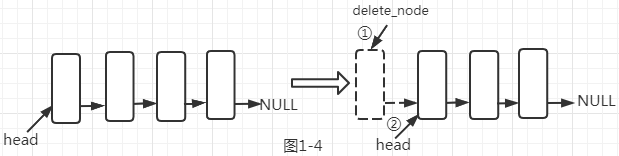
 　　若是第二种情况，我们首先得找到要删除的序号为index的结点的前一个结点，即序号为index-1的结点，然后再进行删除操作，如下图1-5。