go_数据结构_递归_迷宫回溯
1、递归
1.1 递归的应用场景（迷宫回溯问题）
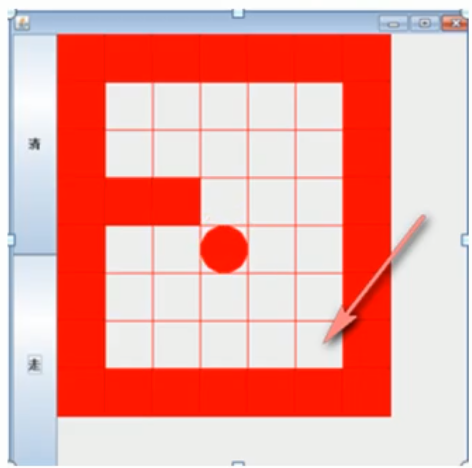
1.2 递归概念
递归就是函数/方法自己调用自己，每次调用时传入不同的变量，递归有助于编程者解决复杂的问题，同时让代码变得简单。
1.3 递归快速入门
1、打印问题
2、阶乘问题
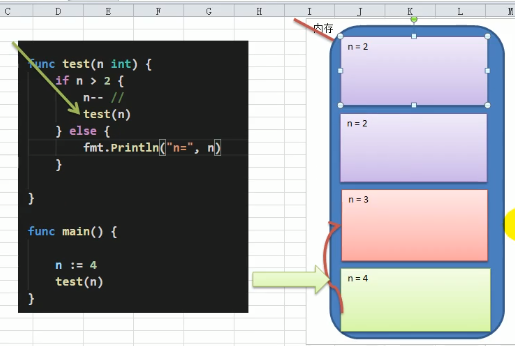
1.4 递归解决问题
1、各种数学问题：n皇后问题、汉诺塔、阶乘问题、迷宫问题等
2、将用栈解决的问题-------》递归代码比较简洁
1.5 递归需要遵守的原则
1、执行一个函数时，就创建一个新的受保护的独立空间（新函数栈）
2、函数的局部变量是独立的，不会互相影响
3、递归必须向退出递归的条件逼近，否则就是无限递归
4、当一个函数执行完毕，或者遇到return，就会返回，遵守谁调用就将结果返回给谁，同时当函数执行完毕或者返回时，该函数就会被系统销毁
1.6 迷宫问题代码实现
package main
import "fmt"
//编写函数，完成迷宫路线
//i，j表示对地图的点进行测试
func setway(mymap *[8][7]int, i, j int) bool {
//[6][5]代表终点
if mymap[6][5] == 2 {
return true
} else {
if mymap[i][j] == 0 {
//假设这个点是通的,但是需要判断 下右上左
mymap[i][j] = 2
if setway(mymap, i+1, j) {
return true
} else if setway(mymap, i, j+1) {
return true
} else if setway(mymap, i+1, j) {
return true
} else if setway(mymap, i, j-1) {
return true
} else { //死路
mymap[i][j] = 3
return false
}
} else {
return false
}
}
}
func main() {
//1、先用二维数组设计一个地图，模拟迷宫
//2、用1 代表墙壁
//3、用0 代表道路
//4、走通的路用2表示
//5、不通的路用3表示
mymap := [8][7]int{}
i, j := 0, 0
for i = 0; i < 7; i++ {
mymap[0][i] = 1
mymap[7][i] = 1
}
for j = 0; j < 8; j++ {
mymap[j][0] = 1
mymap[j][6] = 1
}
mymap[3][1] = 1
mymap[3][2] = 1
//打印地图
for i = 0; i < 8; i++ {
for j = 0; j < 7; j++ {
fmt.Print(mymap[i][j], " ")
}
fmt.Println()
}
setway(&mymap, 1, 1)
fmt.Println("地图走完：：：：")
for i = 0; i < 8; i++ {
for j = 0; j < 7; j++ {
fmt.Print(mymap[i][j], " ")
}
fmt.Println()
}
}
