浅谈 Attention 机制的理解

什么是注意力机制？

注意力机制模仿了生物观察行为的内部过程，即一种将内部经验和外部感觉对齐从而增加部分区域的观察精细度的机制。例如人的视觉在处理一张图片时，会通过快速扫描全局图像，获得需要重点关注的目标区域，也就是注意力焦点。然后对这一区域投入更多的注意力资源，以获得更多所需要关注的目标的细节信息，并抑制其它无用信息。

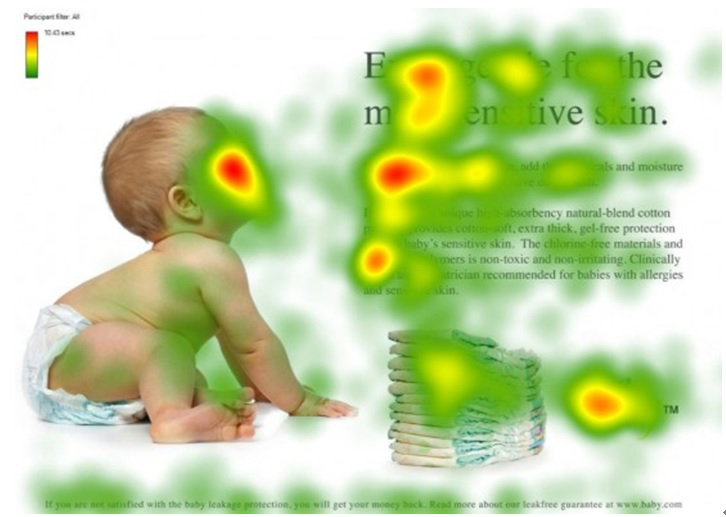
图片来源：深度学习中的注意力机制，其中红色区域表示更关注的区域。

Encoder-Decoder 框架

目前大多数的注意力模型都是依附在 Encoder-Decoder 框架下，但并不是只能运用在该模型中，注意力机制作为一种思想可以和多种模型进行结合，其本身不依赖于任何一种框架。Encoder-Decoder 框架是深度学习中非常常见的一个模型框架，例如在 Image Caption 的应用中 Encoder-Decoder 就是 CNN-RNN 的编码 - 解码框架；在神经网络机器翻译中 Encoder-Decoder 往往就是 LSTM-LSTM 的编码 - 解码框架，在机器翻译中也被叫做 Sequence to Sequence learning 。

所谓编码，就是将输入的序列编码成一个固定长度的向量；解码，就是将之前生成的固定向量再解码成输出序列。这里的输入序列和输出序列正是机器翻译的结果和输出。

为了说明 Attention 机制的作用，以 Encoder-Decoder 框架下的机器翻译的应用为例，该框架的抽象表示如下图：

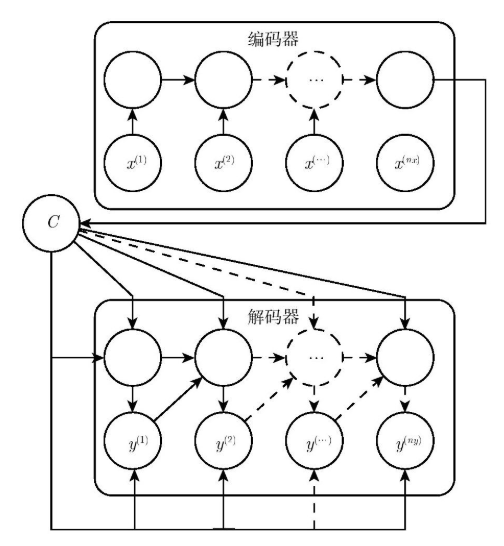
为了方便阐述，在选取 Encoder 和 Decoder 时都假设其为 RNN。在 RNN 中，当前时刻隐藏状态 \(h_t\) 是由上一时刻的隐藏状态 \(h_{t-1}\) 和当前时刻的输入 \(x_t\) 决定的，如公式（1）所示：

\[h_t = f(h_{t-1},x_t)\tag{1} \]

在 编码阶段，获得各个时刻的隐藏层状态后，通过把这些隐藏层的状态进行汇总，可以生成最后的语义编码向量 \(C\) ，如公式（2）所示，其中 \(q\) 表示某种非线性神经网络，此处表示多层 RNN 。

\[C=q(h_1,h_2,\cdots,h_{T_x})\tag{2} \]

在一些应用中，也可以直接将最后的隐藏层编码状态作为最终的语义编码 \(C\)，即满足：

\[C=q(h_1,h_2,\cdots,h_{T_x})=h_{T_x}\tag{3} \]

在 解码阶段，需要根据给定的语义向量 \(C\) 和之前已经生成的输出序列 \(y_1,y_2,\cdots,y_{t-1}\) 来预测下一个输出的单词 \(y_t\)，即满足公式（4）：

\[y_t=\arg \max P(y_t)=\prod_{t=1}^{T}p(y_t|y_1,y_2,\cdots,y_{t-1},C)\tag{4} \]

由于我们此处使用的 Decoder 是 RNN ，所以当前状态的输出只与上一状态和当前的输入相关，所以可以将公式（4）简写成如下形式：

\[y_t=g(y_{t-1},s_{t-1},C)\tag{5} \]

在公式（5）中，\(s_{t-1}\) 表示 Decoder 中 RNN 神经元的隐藏层状态，\(y_{t-1}\) 表示前一时刻的输出，\(C\) 代表的是编码后的语义向量，而 \(g(\cdot)\) 则是一个非线性的多层神经网络，可以输出 \(y_t\) 的概率，一般情况下是由多层 RNN 和 softmax 层组成。

局限性

Encoder-Decoder 框架虽然应用广泛，但是其存在的局限性也比较大。其最大的局限性就是 Encoder 和 Decoder 之间只通过一个固定长度的语义向量 \(C\) 来唯一联系。也就是说，Encoder 必须要将输入的整个序列的信息都压缩进一个固定长度的向量中，存在两个弊端：一是语义向量 C 可能无法完全表示整个序列的信息；二是先输入到网络的内容携带的信息会被后输入的信息覆盖掉，输入的序列越长，该现象就越严重。这两个弊端使得 Decoder 在解码时一开始就无法获得输入序列最够多的信息，因此导致解码的精确度不够准确。

Attention 机制

在上述的模型中，Encoder-Decoder 框架将输入 \(X\) 都编码转化为语义表示 \(C\)，这就导致翻译出来的序列的每一个字都是同权地考虑了输入中的所有的词。例如输入的英文句子是：Tom chase Jerry，目标的翻译结果是：汤姆追逐杰瑞。在未考虑注意力机制的模型当中，模型认为 汤姆 这个词的翻译受到 Tom，chase 和 Jerry 这三个词的同权重的影响。但是实际上显然不应该是这样处理的，汤姆 这个词应该受到输入的 Tom 这个词的影响最大，而其它输入的词的影响则应该是非常小的。显然，在未考虑注意力机制的 Encoder-Decoder 模型中，这种不同输入的重要程度并没有体现处理，一般称这样的模型为 分心模型。

而带有 Attention 机制的 Encoder-Decoder 模型则是要从序列中学习到每一个元素的重要程度，然后按重要程度将元素合并。因此，注意力机制可以看作是 Encoder 和 Decoder 之间的接口，它向 Decoder 提供来自每个 Encoder 隐藏状态的信息。通过该设置，模型能够选择性地关注输入序列的有用部分，从而学习它们之间的“对齐”。这就表明，在 Encoder 将输入的序列元素进行编码时，得到的不在是一个固定的语义编码 C ，而是存在多个语义编码，且不同的语义编码由不同的序列元素以不同的权重参数组合而成。一个简单地体现 Attention 机制运行的示意图如下：

定义：对齐

对齐是指将原文的片段与其对应的译文片段进行匹配。

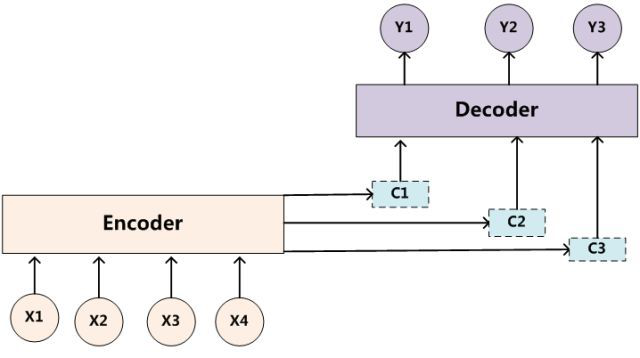
在 Attention 机制下，语义编码 C 就不在是输入序列 \(X\) 的直接编码了，而是各个元素按其重要程度加权求和得到的，即：

\[C_i=\sum_{j=0}^{T_x}{a_{ij}f(x_j)}\tag{6} \]

在公式（6）中，参数 \(i\) 表示时刻， \(j\) 表示序列中的第 \(j\) 个元素， \(T_x\) 表示序列的长度， \(f(\cdot)\) 表示对元素 \(x_j\) 的编码。\(a_{ij}\) 可以看作是一个概率，反映了元素 \(h_j\) 对 \(C_i\) 的重要性，可以使用 softmax 来表示：

\[a_{ij}=\frac{exp(e_{ij})}{\sum_{k=1}^{T_x}exp(e_{ik})}\tag{7} \]

这里 \(e_{ij}\) 正是反映了待编码的元素和其它元素之间的匹配度，当匹配度越高时，说明该元素对其的影响越大，则 \(a_{ij}\) 的值也就越大。

因此，得出 \(a_{ij}\) 的过程如下图：

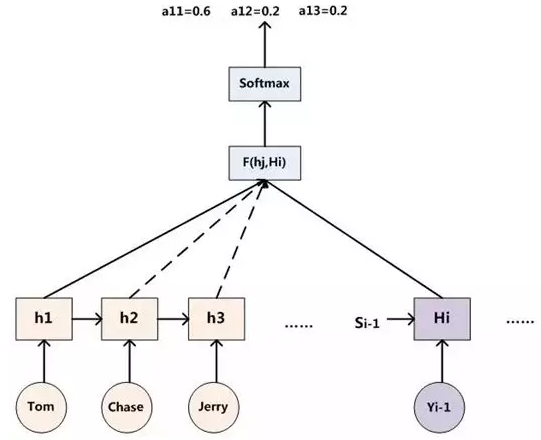
其中，\(h_i\) 表示 Encoder 的转换函数，\(F(h_j,H_i)\) 表示预测与目标的匹配打分函数。将以上过程串联起来，则注意力模型的结构如下图所示：

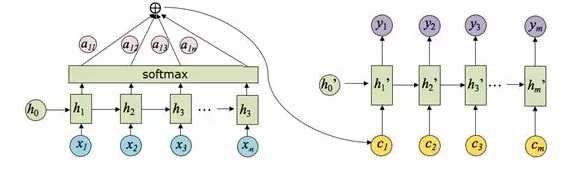
Attention 原理

到目前为止，相信各位客官对 Attention 机制的思想和作用都有了一定的了解。接下来，我们将对 Attention 机制的具体实现原理进行剖析。

Attention 机制的一个重点就是获得 attention value，即机器翻译中的语义编码 \(C_i\)。在上一节中我们知道该值是通过输入元素按照不同的权重参数组合而成的，所以我们可以将其定义为一个 attention 函数，比较主流的 attention 函数的机制是采用键值对查询的方式，其工作实质如下图所示：

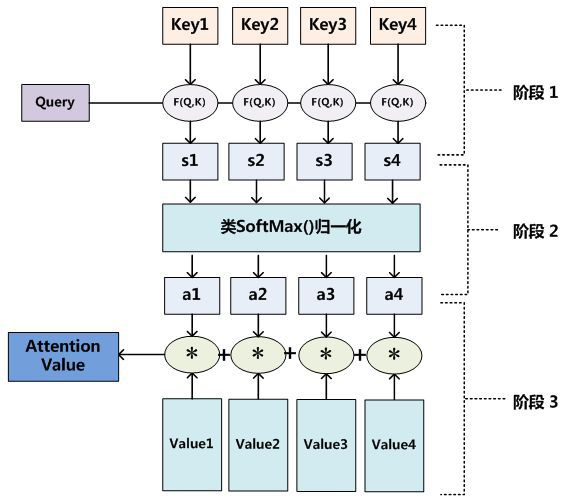
在自然语言任务中，往往 Key 和 Value 是相同的。需要注意的是，计算出来的 attention value 是一个向量，代表序列元素 \(x_j\) 的编码向量，包含了元素 \(x_j\) 的上下文关系，即同时包含全局联系和局部联系。全局联系很好理解，因为在计算时考虑了该元素与其他所有元素的相似度计算；而局部联系则是因为在对元素 \(x_j\) 进行编码时，重点考虑与其相似度较高的局部元素，尤其是其本身。

阅读到一篇有关 动画图解Attention机制 的文章，这里主要是对 Attention 层的实现做下总结，详细内容请查看原文。注意力机制可以看作是神经网络架构中的一层神经网络，注意力层的实现可以分为 6 个步骤。

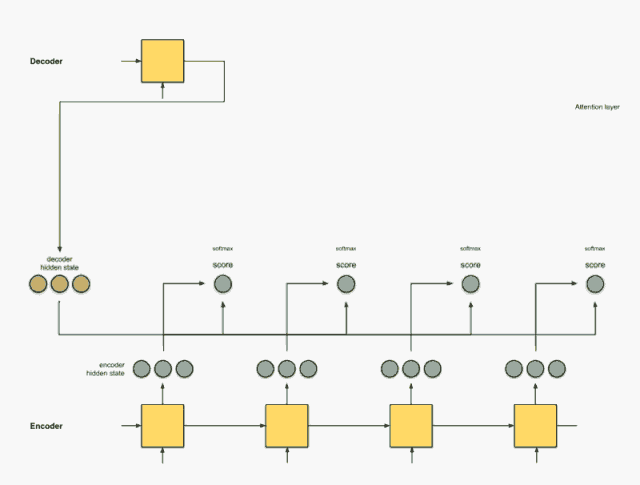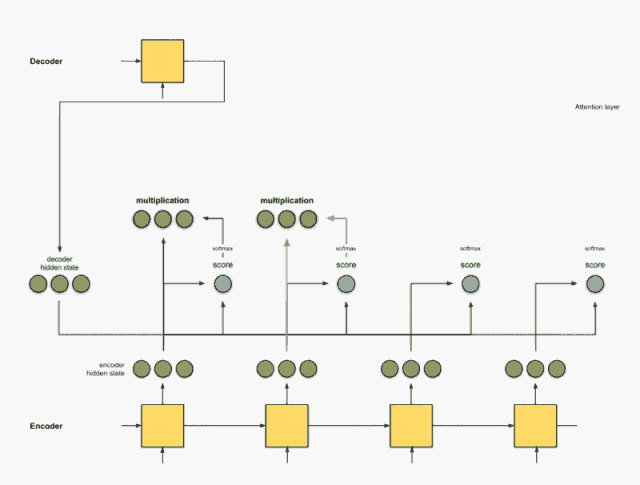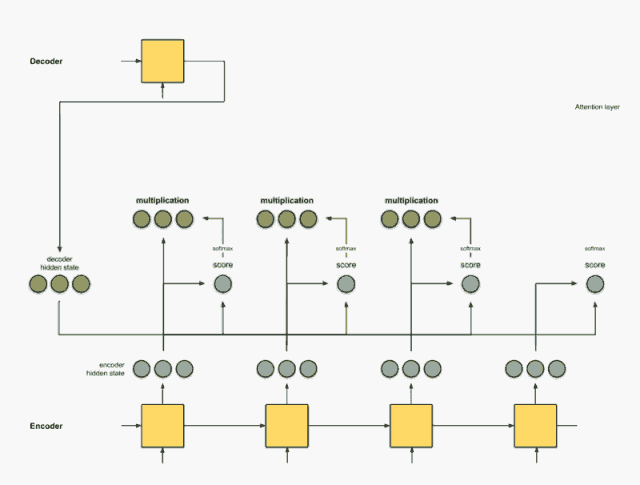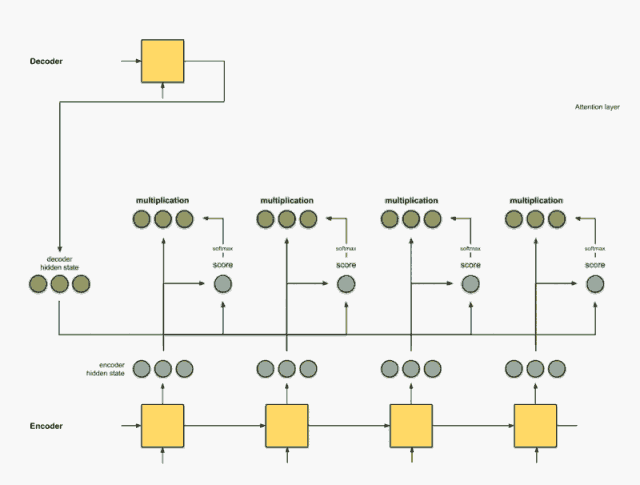
Step 0：准备隐藏状态

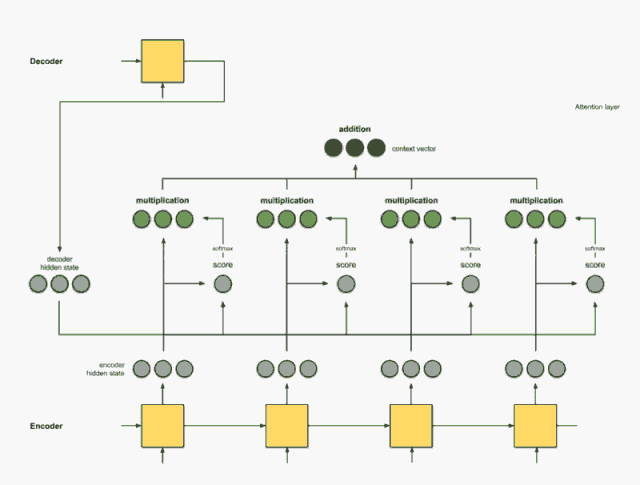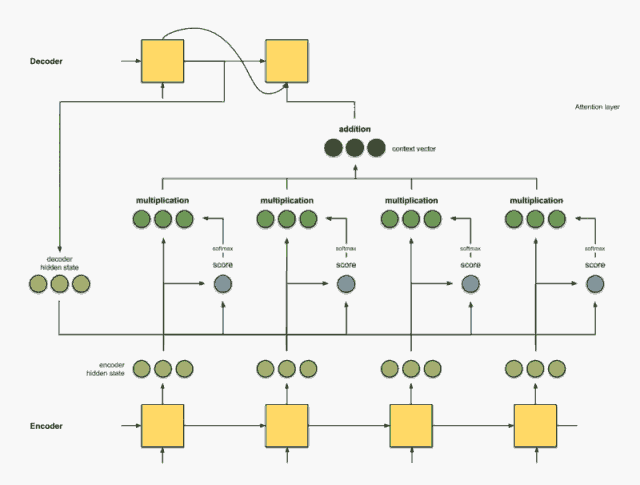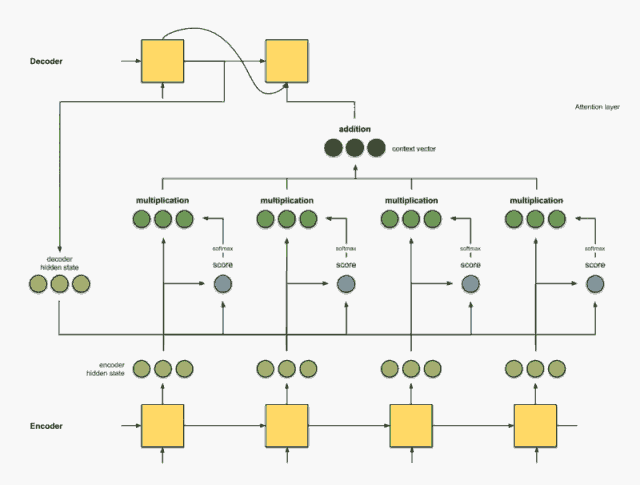
首先准备第一个 Decoder 的隐藏层状态（红色）和所有可用的 Encoder 隐藏层状态（绿色）。在示例中，有 4 个 Encoder 隐藏状态和 1 个 Decoder 隐藏状态。

Step 1：得到每一个 Encoder 隐藏状态的得分

分值（score）由 score 函数来获得，最简单的方法是直接用 Decoder 隐藏状态和 Encoder 中的每一个隐藏状态进行点积。

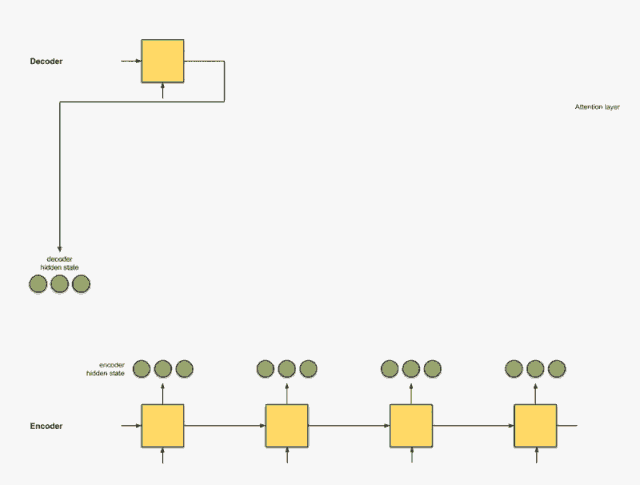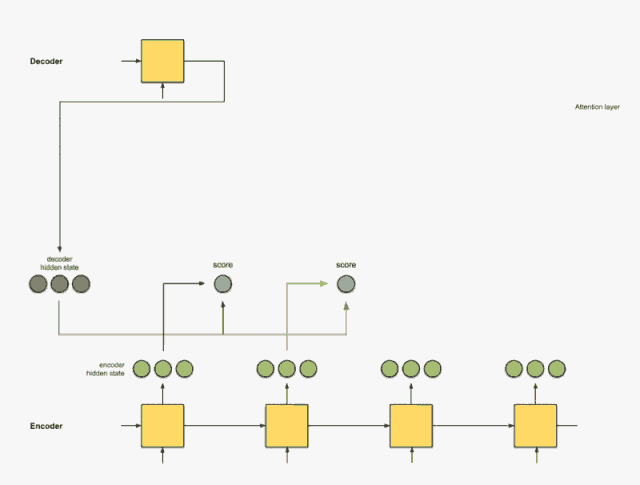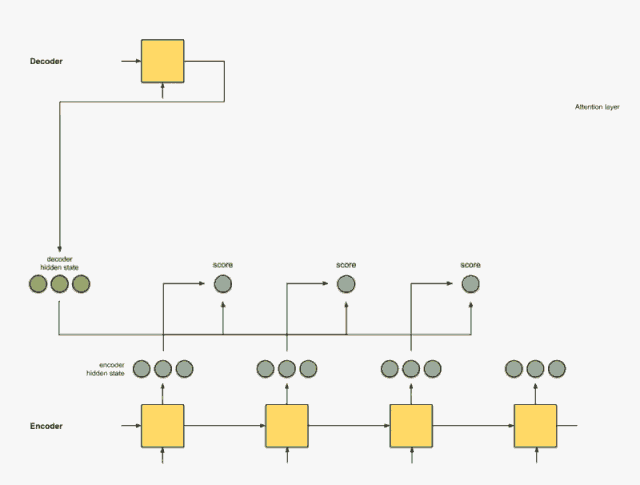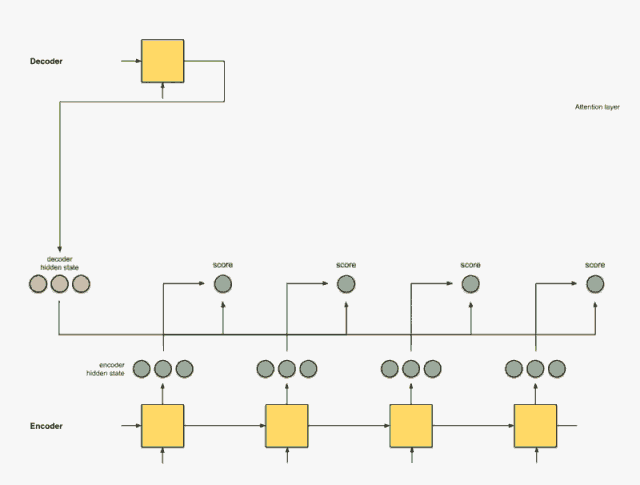
假设 Decoder 中的隐藏状态为 [5, 0, 1]，分别与 Encoder 中的每个隐藏状态做点积，得到第二个隐藏状态的分值最高，说明下一个要解码的元素将受到当前这种隐藏状态的严重影响。

decoder_hidden = [10, 5, 10]
encoder_hidden score
---------------------
     [0, 1, 1]     15 (= 10×0 + 5×1 + 10×1, the dot product)
     [5, 0, 1]     60
     [1, 1, 0]     15
     [0, 5, 1]     35

Step 2：将所有得分送入 softmax 层

该部分实质上就是对得到的所有分值进行归一化，这样 softmax 之后得到的所有分数相加为 1。而且能够使得原本分值越高的隐藏状态，其对应的概率也越大，从而抑制那些无效或者噪音信息。

通过 softmax 层后，可以得到一组新的隐藏层状态分数，其计算方法即为公式（7）：\(a_{ij}=\frac{exp(e_{ij})}{\sum_{k=1}^{T_x}exp(e_{ik})}\)。注意，此处得到的分值应该是浮点数，但是由于无限接近于 0 和 1，所以做了近似。

encoder_hidden score score^
-----------------------------
     [0, 1, 1]     15       0
     [5, 0, 1]     60       1
     [1, 1, 0]     15       0
     [0, 5, 1]     35       0

Step 3：用每个 Encoder 的隐藏状态乘以 softmax 之后的得分

通过将每个编码器的隐藏状态与其softmax之后的分数(标量)相乘，我们得到 对齐向量 或标注向量。这正是对齐产生的机制

加权求和之后可以得到新的一组与 Encoder 隐藏层状态对应的新向量，由于之后第二个隐藏状态的分值为 1 ，而其它的为0，所以得到的新向量也只有第二个向量有效。

 encoder score score^ alignment
 ---------------------------------
 [0, 1, 1]   15     0   [0, 0, 0]
 [5, 0, 1]   60     1   [5, 0, 1]
 [1, 1, 0]   15     0   [0, 0, 0]
 [0, 5, 1]   35     0   [0, 0, 0]

Step 4：将所有对齐的向量进行累加

对对齐向量进行求和，生成 上下文向量 。上下文向量是前一步的对齐向量的聚合信息。

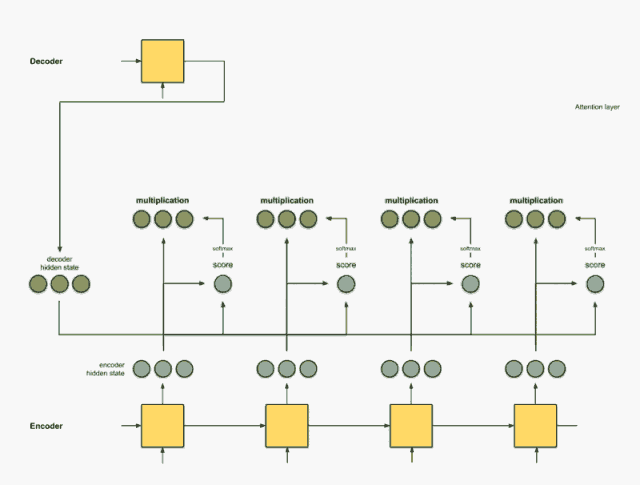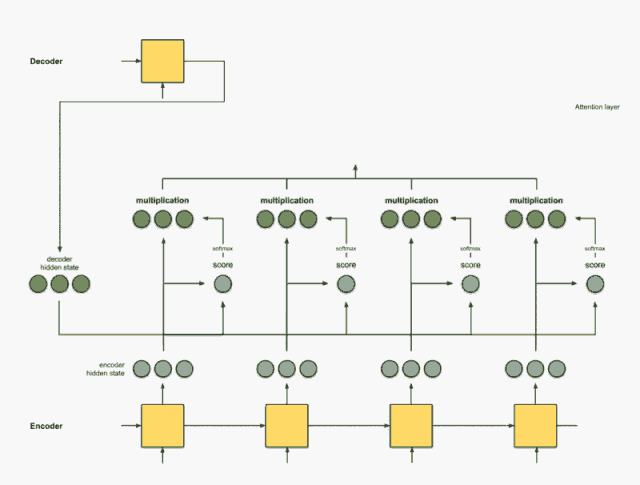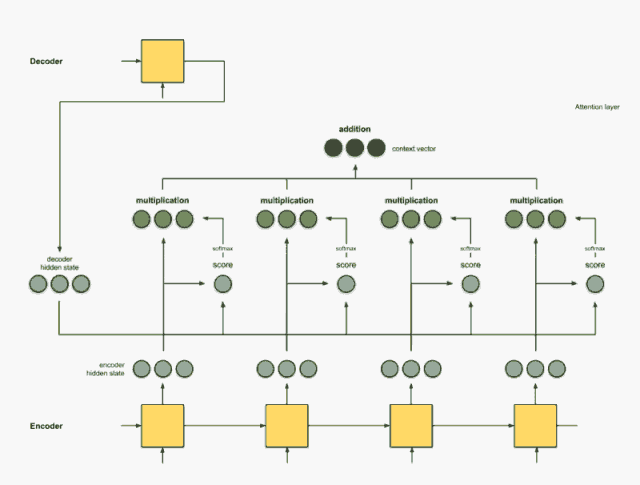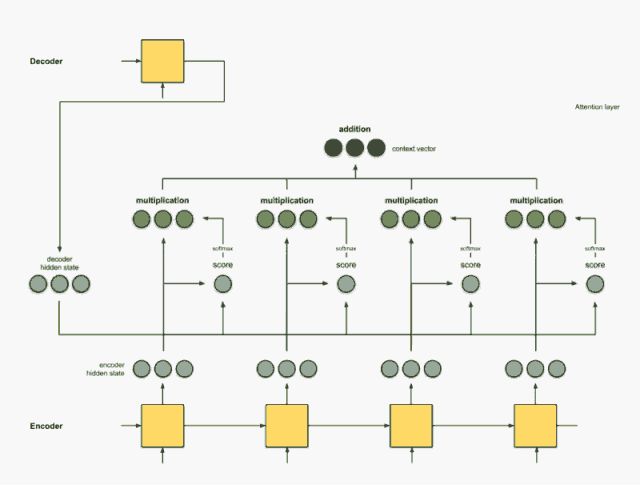
该步骤其实就对应了公式（6），得到最终的编码后的向量来作为 Decoder 的输入，其编码后的向量为 [5, 0, 1]。

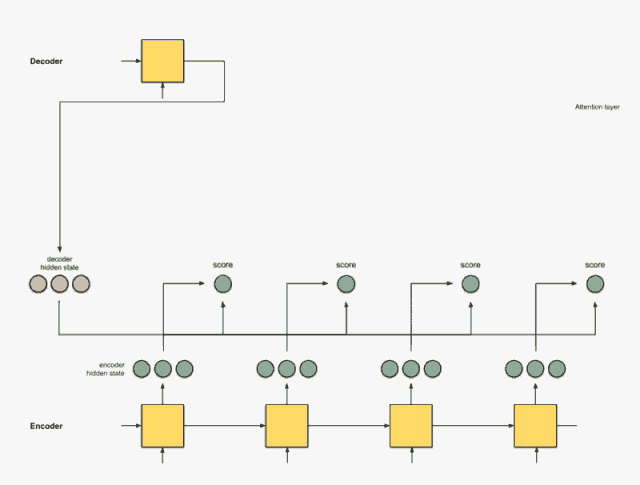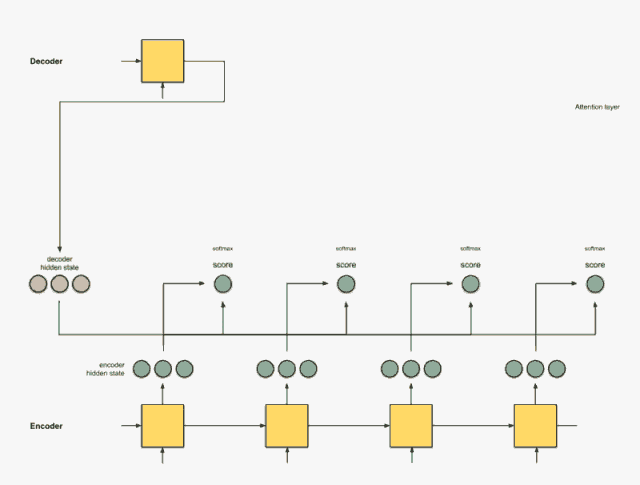
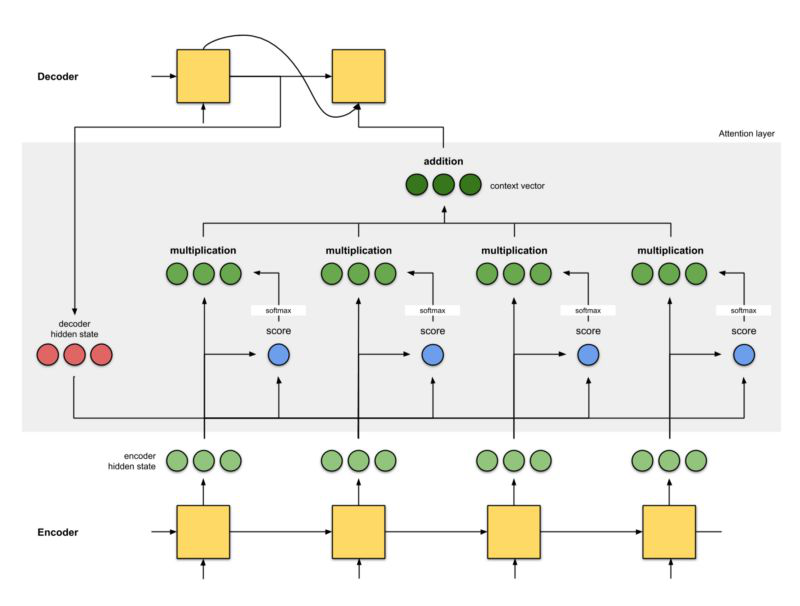
Step 5：把上下文向量送到 Decoder 中

通过将上下文向量和 Decoder 的上一个隐藏状态一起送入当前的隐藏状态，从而得到解码后的输出。

最终得到完整的注意力层结构如下图所示：

Attention 机制的优劣

相比于传统的 RNN 和 CNN，attention 机制具有如下优点：

• 一步到位的全局联系捕捉，且关注了元素的局部联系；attention 函数在计算 attention value 时，是进行序列的每一个元素和其它元素的对比，在这个过程中每一个元素间的距离都是一；而在时间序列 RNNs 中，元素的值是通过一步步递推得到的长期依赖关系获取的，而越长的序列捕捉长期依赖关系的能力就会越弱。

• 并行计算减少模型训练时间；Attention 机制每一步的计算都不依赖于上一步的计算结果，因此可以并行处理。

• 模型复杂度小，参数少

但 attention 机制的缺点也比较明显，因为是对序列的所有元素并行处理的，所以无法考虑输入序列的元素顺序，这在自然语言处理任务中比较糟糕。因为在自然语言中，语言的顺序是包含了十分多的信息的，如果缺失了该部分的信息，则得到的结果往往会大大折扣。

总结

简而言之，Attention 机制就是对输入的每个元素考虑不同的权重参数，从而更加关注与输入的元素相似的部分，而抑制其它无用的信息。其最大的优势就是能一步到位的考虑全局联系和局部联系，且能并行化计算，这在大数据的环境下尤为重要。同时，我们需要注意的是 Attention 机制作为一种思想，并不是只能依附在 Encoder-Decoder 框架下的，而是可以根据实际情况和多种模型进行结合。

该文仅是对 Attention 机制的思想和原理进行了分析，在具体的实现上还有许多的细节信息，包括和框架的结合方式，具体的数学计算，并行计算的过程以及具体的代码实现等，后续会持续更新 Attention 机制这些部分的内容。

参考资料

• 深度学习中的注意力机制
• 浅谈 Attention 机制的理解
• Attention 机制简单总结
• 什么是自注意力机制？
• 动画图解Attention机制，让你一看就明白