Spark 中的机器学习库及示例
MLlib 是 Spark 的机器学习库，旨在简化机器学习的工程实践工作，并方便扩展到更大规模。MLlib 由一些通用的学习算法和工具组成，包括分类、回归、聚类、协同过滤、降维等，同时还包括底层的优化原语和高层的管道 API。具体来说，主要包括以下几方面的内容：
- 机器学习算法：常用的学习算法，如分类、回归、聚类和协同过滤；
- 特征化工具：特征提取、转化、降维和特征选择等工具；
- 管道：由于构建、评估和调整机器学习管道的工具；
- 持久性：保存和加载算法，模型和管道；
- 实用工具：线性代数，统计和数据处理等工具。
DataFrame-based API
从 Spark 2.0 开始，RDD-based API 已经进入维护模式，不再增加新的功能，并期望在 Spark 3.0 中移除。而 DataFrame-based API 成为 Spark 中的机器学习的主要 API。主要原因有以下几点：
-
DataFrames 提供比 RDDs 更加用户友好的 API，好处包括支持多种 Spark 数据源，SQL/DataFrame 查询，Tungsten 和 Catalyst 优化以及跨语言的统一 API；
-
DataFrame-based API 为 MLlib 提供了统一的跨多种 ML 算法和多种语言的 API；
-
DataFrames 有助于实用的 ML 管道，特别是功能转换。
使用 ML Pipeline API 可以很方便的把数据处理，特征转换，正则化，以及多个机器学习算法联合起来，构建一个单一完整的机器学习流水线。这种方式给我们提供了更灵活的方法，更符合机器学习过程的特点，也更容易从其他语言迁移。
机器学习工具
示例（逻辑回归）
逻辑回归是预测分类结果的常用方法。广义线性模型的一个特例是预测结果的概率。在 spark.ml 中，逻辑回归可以用 binomial logistic regression 来预测二元结果，或者使用 multinomial logistic regression 来预测多类结果。使用 family 参数在这两个算法之间进行选择，或者保持不设置，Spark 将推断出正确的变量。
from pyspark.ml.classification import LogisticRegression
# Load training data
training = spark.read.format("libsvm").load("data/mllib/sample_libsvm_data.txt")
lr = LogisticRegression(maxIter=10, regParam=0.3, elasticNetParam=0.8)
# Fit the model
lrModel = lr.fit(training)
# Print the coefficients and intercept for logistic regression
print("Coefficients:" + str(lrModel.coefficients))
print("Intercept:" + str(lrModel.intercept))
# We can also use the multinomial family for binary classification
mlr = LogisticRegression(maxIter=10, regParam=0.3, elasticNetParam=0.8, family="multinomial")
# Fit the model
mlrModel = mlr.fit(training)
# Print the coefficients and intercepts for logistic regression with multinomial family
print("Multinomial coefficients:" + str(mlrModel.coefficientMatrix))
print("Multinomial intercepts:" + str(mlrModel.interceptVector))
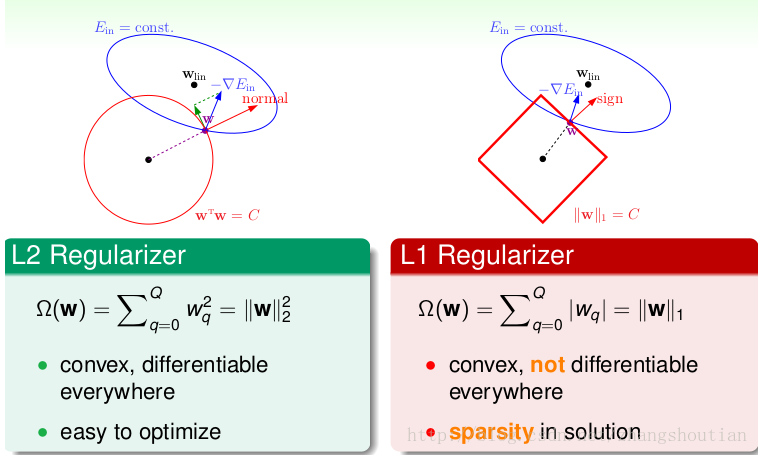
其中，libsvm 为一种数据格式，具体形式可以参考：libsvm。regParam 定义了正则化项的权重参数，elasticNetParam 表示选择的正则化项。假设定义的正则化项如下：
则 regParam 参数正是对应了参数 \(\lambda\)，而 elasticNetParam 则是对应了参数 \(\alpha\)，则有如下情况：
- 当 \(\alpha=0\) 时，惩罚项为 L2 正则，默认情况；
- 当 \(\alpha=1\) 时，惩罚项为 L1 正则；
- 当 \(0<\alpha<1\) 时，惩罚项为 L1 正则和 L2 正则的混合；
L1 和 L2 正则的主要目的是解决模型的过拟合问题，具体的形式为：
