我们的可可西里 题解———2019.10.18

我们的可可西里

(keke.cpp)

转眼到了2008年的6月9日，盼望已久的高考结束了。我们踏上了向西的旅程（本来是想写西去之路，可是考虑不太妥当）。可可西里，多么诱人的名词，充满了奇幻的色彩和自然的淳朴。从可可西里徒步走回家的决定是在1年半前定下的，而现在，终于可以实现那个钩过手指的预定。我们的可可西里。。。

   在回家的路上，疯子和蚊子看到了许多可爱的藏羚羊，无意之中疯子和蚊子发现藏羚羊的居住地的分布也是有规律的，虽然疯子和蚊子早就听说藏羚羊是一种群体性很强又有超高IQ的动物，但是还是为它们的居住地分布规律感到惊叹。经过细心的观察，疯子和蚊子发现，如果假设一个藏羚羊群体有N只羊，就可以把它们的领地当做一个N*N的方阵，在这个方阵上第I列的第I 行都有一个圣地，它们不会居住在圣地，同时每行每列只能居住一只羚羊。于是他们很快算出一个有N只羊的藏羚羊群体的居住地分布方法数。

 

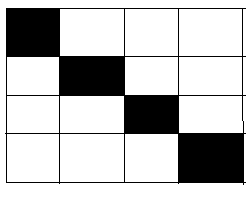
这是圣地的一种排列方法

 

 

 

 

 一个整数N 代表藏羚羊的个数 INPUT:

OUTPUT:

  一个整数sum代表方法数 

输入样例：

4

输出样例：

9

对于30%的数据，n<=10

对于全部数据 n<=1000

 

 

我们的可可西里

错排问题。

瑞士数学家欧拉推出个公式

 f(n)=n!(1/2!-1/3!+1/4!+..+(-1)^n/n!)

我不是瑞士数学家。所以我给大家一个递推公式。

First

易得f[1]:=0;f[2]:=1;

Second

假设我们已经得到f[k-2],f[k-1].现在想求f[k].

1.K可以与从1在K -1 中任意一个棋子I 交换，这样固定了2个棋子，剩下K-2棋子的排列方法数为f[K-2].那么按照这种K和1到K-1中交换棋子可以得到的方案总数为(K-1)*f[K-2];

2.K可以放在1到K-1中的任何一个位置I，并且I 不放到K个位置上，其实这样就等效于f[K-1]种方法，所以这种策略的总和为(K-1)*f[K-1].

所以我们便得到了个递推公式f[K]:=(K-1)*(f[K-1]+f[K-2]);

当然数据范围需要应用到高精度。

 

自己推不出来那么神奇的公式

那就暴力把前30%的数据做出来

然后就可以请数竞的大佬来找规律了

↓ 我推的 ↓

f[1]=0,f[2]=1;f[3]=2
f[i]=i*f[i-1]
if(i%2)f[i]--;
else f[i]++;

考试测只有80分，后来发现，竟是数组开的不够大

我枯了

满分代码：

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
using namespace std;
long long ans;
int n,l;
int f[1001][10001];
void suan(int b) {
    for(int i=1; i<=10000; i++)
        f[l][i]=f[l-1][i]*b;
    for(int i=1; i<=10005; i++)
        if(f[l][i]>=10) {
            f[l][i+1]+=f[l][i]/10;
            f[l][i]%=10;
        }
    return ;
}
int main() {
    freopen("keke.in","r",stdin);
    freopen("keke.out","w",stdout);
    int n;
    cin>>n;
    f[1][1]=0,f[2][1]=1,f[3][1]=2;
    for(l=4; l<=n; l++) {
        suan(l);
        if(l%2)f[l][1]--;
        else f[l][1]++;
    }
    for(int i=1; i<=10005; i++)
        if(f[n][i]>=10) {
            f[n][i+1]+=f[n][i]/10;
            f[n][i]%=10;
        }
    int t=10000;
    bool a=false;
    if(n==1) {
        cout<<0;
        fclose stdin;
        fclose stdout;
        return 0;
    }
    while(t) {
        if(f[n][t]==0&&!a) {
            t--;
            continue;
        } else {
            a=true;
            cout<<f[n][t];
        }
        t--;
    }
    fclose stdin;
    fclose stdout;
    return 0;
}