Problem A. 最近公共祖先 ———2019.10.12
我亲爱的学姐冒险跑去为我们送正解
但是,,,,
阿龙粗现了!
cao,,

考场期望得分:20 实际得分:20
Problem A. 最近公共祖先 (commonants.c/cpp/pas)
最近公共祖先(Lowest Common Ancestor,LCA)是指在一个树中同时拥有给定的两个点作为后
代的最深的节点。
为了学习最近公共祖先,你得到了一个层数为 n + 1 的满二叉树,其中根节点的深度为 0,其他
节点的深度为父节点的深度 +1 。你需要求出二叉树上所有点对 (i,j),(i,j 可以相等,也可以 i > j)
的最近公共祖先的深度之和对 10 9 + 7 取模后的结果。
Input
一行一个整数 n 。
Output
一行一个整数表示所有点对 (i,j),(i,j 可以相等,也可以 i > j)的最近公共祖先的深度之和对
10 9 + 7 取模后的结果。

Notes
样例 1 解释:

树一共有 7 个节点(一个根节点和两个子节点) ,其中 (4,4),(5,5),(6,6),(7,7) 共 4 对的最近公共
祖先深度为 2,(4,2),(2,4),(5,2),(2,5),(5,4),(4,5),(2,2),(6,3),(3,6),(3,7),(7,3),(6,7),(7,6),(3,3) 共 14 对最
近公共祖先深度是 1 ,其他的点对最近公共祖先深度为 0 ,所以答案为 22 。

思路呢,,大概就是这样的:
算法1:
N<=10
直接暴力求树上两点的LCA
期望得分:20
(大概就是我的那20分吧)
代码~:

1 #include<cmath> 2 #include<cstdio> 3 #include<iostream> 4 using namespace std; 5 int n; 6 const int mod=1e9+7; 7 int deep[10000]; 8 long long ans; 9 void dfs(int i,long long t) { 10 if(i>n) return; 11 deep[t]=i; 12 dfs(i+1,t*2),dfs(i+1,t*2+1); 13 } 14 long long lca(long long i,long long j) { 15 while(1) { 16 if(i==j)break; 17 if(i<j)swap(i,j); 18 i/=2; 19 } 20 return deep[i]; 21 } 22 long long tot; 23 int main() { 24 freopen("commonants.in","r",stdin); 25 freopen("commonants.out","w",stdout); 26 cin>>n; 27 tot=pow(2,n+1)-1; 28 dfs(0,1); 29 for(int i=1; i<=tot; i++) 30 for(int j=1; j<=tot; j++) { 31 int k=lca(i,j); 32 ans+=k; 33 ans%=mod; 34 } 35 cout<<ans; 36 fclose stdin; 37 fclose stdout; 38 return 0; 39 }
算法2:

代码:没得~
算法三:

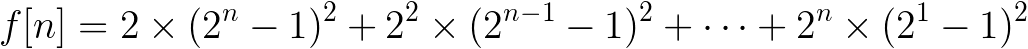

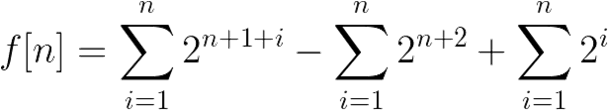
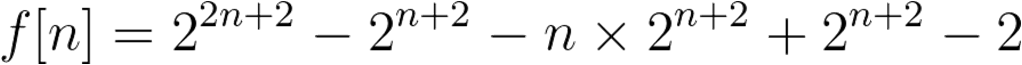

借土蛋 的代码一用

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 typedef long long ll; 5 const ll mod = 1e9 + 7; 6 ll qpow(ll a, ll b){ 7 ll ret = 1; 8 for(; b; b >>= 1, a = a * a % mod){ 9 if(b & 1) ret = ret * a % mod; 10 } 11 return ret; 12 } 13 ll n; 14 ll f[1000005]; 15 int main(){ 16 freopen("commonants.in", "r", stdin); 17 freopen("commonants.out", "w", stdout); 18 19 cin >> n; 20 printf("%lld\n", (qpow(2, 2 * n + 2) - (4 * n % mod + 2) * qpow(2, n) % mod + mod - 2 + mod) % mod); 21 return 0; 22 }


