Problem 2 旅行计划 (travelling .cpp)———2019.10.6
lth tql,lzpclxf tql Orz
Problem 2 旅行计划 (travelling.cpp)
【题目描述】
小 Z 打算趁着暑假,开启他的旅行计划。但与其他同学不同的是,小 Z 旅
行时并不关心到达了哪个网红景点打了哪些卡。小 Z 更关注沿路的风光,而且
小 Z 觉得,尽管多次到达同一个地方,但如果来时的路不一样,也是别有一番
风味。
小 Z 事先准备了一份地图,地图上给出了 N 个小 Z 心仪的城市,依次编号
1…N,以及 M 条连接两个城市的路,编号 1…M。小 Z 打算把 M 条路都走一遍且
仅一遍,但他发现这样的路线可能是不存在的。于是他打算,当他走到一个城
市后发现从这个城市出发的道路他都已经走过了,他便会坐飞机到另一个城市,
然后继续他的旅行。
现在小 Z 想知道,在最好的路线计划下,他至少要坐多少趟飞机。
【输入格式】
第一行为测试数据组数 T(1≤T≤10) 。
每组测试数据的第一行为城市数 N 及道路数 M。
接下来 M 行,每行两个整数 x 和 y,表示一条连接城市 x 和城市 y 的双向
道路。
【输出格式】
对于每组测试数据,输出第一行包含一个整数 K,表示小 Z 至少要坐多少
趟飞机。
接下来 K+1 行,第 i 行输出小 Z 的第 i 段行程。若第 i 段行程经过 x 条道
路,则先输出 x,然后输出 x 个整数,分别表示路线经过的道路的编号。若是
正向通过第 i 条道路,则输出 i,否则输出-i。
若有多组方案,输出任意一组。
【样例输入】
1
3 3
1 2
1 3
2 3
【样例输出】
0
3 1 3 -2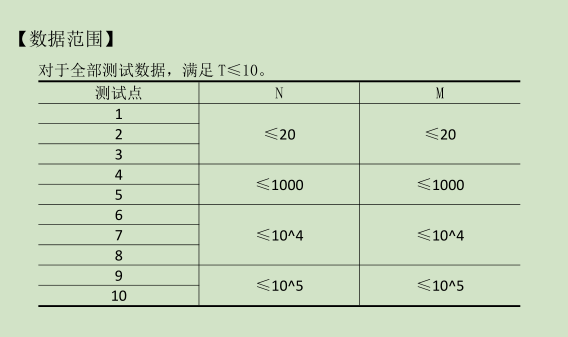
(复制不下来,就扣下来吧)
每个连通块显然是独立的。对于一个连通块(除了单个点的),如果奇度数点个数 为 k,
那么至少需要 max(k/2,1)条路径。这是因为在一个无向图中,将两个度数为奇数的
点连起来,就可以消去两个奇数点。所以如果一个无向图要有欧拉回路(全部点的度数全
为偶数),只要加 k/2 条边就可以了。于是乎,我们只要将一个连通块变成欧拉图,搜一
遍得到路径,再将我们人为添加的边删掉,剩下的就是这个连通块的"笔画"了。 这里为
什么一定变成欧拉回路而不是欧拉通路,其实这里欧拉回路和欧拉通路都是 可以的,得
到的答案是一样的。主要是算法实现上的问题,如果变成欧拉通路,就一定得 从剩下的
两个奇数点出发,终止。至于为什么这里加 k/2 条边后扫出的结果删掉多加的边 就是答
案,并且这个答案=max(k/2,1)呢?这是因为一个图中,我们从奇数点开始走,停止 的也
一定是在奇数点,那么再一遍遍不重复地从图中走出一条条类似前面地路径(奇数点 开始
,奇数点结束)然后我们将这些路径地终点连接下一条路径的起点(多加的边),这样又 因为
每一条路径的起止点都为奇数点,一条边删去两个奇数点。所以最终把他们连成欧拉 回路所需的边的数量就是 k/2。

1 #include<iostream> 2 #include<cstdio> 3 #include<vector> 4 #include<cstring> 5 using namespace std; 6 const int N=1000005; 7 vector<int> ans[N]; 8 int T,n,m,tot=1,head[N],vis[N],in[N],cnt; 9 struct node { 10 int to,nex,flag,id; 11 } a[N>>2]; 12 inline int read() {//快读 13 int x=0,f=1; 14 char ch=getchar(); 15 while(ch<'0'||ch>'9') { 16 if(ch=='-')f=-1; 17 ch=getchar(); 18 } 19 while(ch>='0'&&ch<='9') 20 x=(x<<3)+(x<<1)+(ch^48),ch=getchar(); 21 return x*f; 22 } 23 void add(int x,int y,int id) {//加边 24 a[++tot].to=y; 25 a[tot].nex=head[x]; 26 a[tot].flag=0; 27 a[tot].id=id; 28 head[x]=tot; 29 } 30 void dfs(int x) { 31 vis[x]=1; 32 for(int i=head[x]; i; i=a[i].nex) { 33 int y=a[i].to,emm=a[i].flag; 34 if(!emm) { 35 a[i].flag=a[i^1].flag=1; 36 dfs(y); 37 if(a[i].id)ans[cnt].push_back(-a[i].id); 38 else cnt++; 39 } 40 } 41 } 42 int main() { 43 // freopen("travelling.in","r",stdin); 44 // freopen("travelling.out","w",stdout); 45 T=read(); 46 while(T--) { 47 for(int i = 1; i <= cnt; i ++) ans[i].clear(); 48 tot=1,cnt=0; 49 memset(head,0,sizeof(head)); 50 memset(vis,0,sizeof(vis)); 51 memset(in,0,sizeof(in));//多组数据注意清空数组 52 n=read(); 53 m=read(); 54 for(int i=1,x,y; i<=m; i++) { 55 x=read(); 56 y=read(); 57 add(x,y,i); 58 add(y,x,-i); 59 in[x]++,in[y]++; 60 } 61 int now=0; 62 for(int i=1; i<=n; i++) 63 if(in[i]%2==1) { 64 if(now) { 65 add(i,now,0); 66 add(now,i,0); 67 now=0; 68 } else now=i; 69 } 70 for(int i=1; i<=n; i++) 71 if(!vis[i]&&in[i]%2) { 72 cnt++; 73 dfs(i); 74 cnt--;//回溯 75 } 76 for(int i=1; i<=n; i++) 77 if(!vis[i]&&in[i]) 78 cnt++,dfs(i); 79 //输出 80 printf("%d\n",cnt - 1); 81 for(int i=1; i<=cnt; i++) { 82 printf("%d ",ans[i].size()); 83 for(int j=0; j<ans[i].size(); j++) 84 printf("%d ",ans[i][j]); 85 printf("\n"); 86 } 87 printf("\n"); 88 } 89 // fclose(stdin); 90 // fclose(stdout); 91 return 0; 92 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号