AcWing算法提高课 树形dp 树的中心

AcWing 1073. 树的中心 

#include<bits/stdc++.h>

using namespace std;
typedef long long LL;

vector<int> adj[10010];
vector<int> w[10010];
int p[10010];
int wp[10010];
LL dis1[10010];
LL dis2[10010];
int next1[10010];
int next2[10010];
LL udis[10010];
LL res=1e15;
int DFS(int node,int parent)
{
    p[node]=parent;

    LL d1=0,d2=0;
    LL nxt1=-1,nxt2=-1;
    for(int i=0;i<adj[node].size();i++)
    {
        int nxt=adj[node][i];
        if(nxt!=p[node])
        {
            
            LL d=w[node][i]+DFS(nxt,node);
            if(d>=d1) d2=d1,nxt2=nxt1,d1=d,nxt1=nxt;
            else if(d>d2) d2=d,nxt2=nxt;
        }
        else
        {
            wp[node]=w[node][i];
        }
    }
    dis1[node]=d1;
    dis2[node]=d2;
    next1[node]=nxt1;
    next2[node]=nxt2;

    return d1;

}
void DFS(int node)
{
    if(p[node]<1)
    {
        udis[node]=0;
        res=min(res,dis1[node]);
    }
    else
    {
        udis[node]=wp[node];
        if(next1[p[node]]==node)
        {
            udis[node]+=max(udis[p[node]],dis2[p[node]]);
        }
        else
        {
            udis[node]+=max(udis[p[node]],dis1[p[node]]);
        }

        res=min(res,max(dis1[node],udis[node]));
    }
    for(int i=0;i<adj[node].size();i++)
    {
        int nxt=adj[node][i];
        if(nxt!=p[node])
            DFS(nxt);
    }
    
}
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<n;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        adj[a].push_back(b);
        w[a].push_back(c);
        adj[b].push_back(a);
        w[b].push_back(c);
    }
    DFS(1,-1);
    DFS(1);
    cout<<res<<endl;
    
}

 

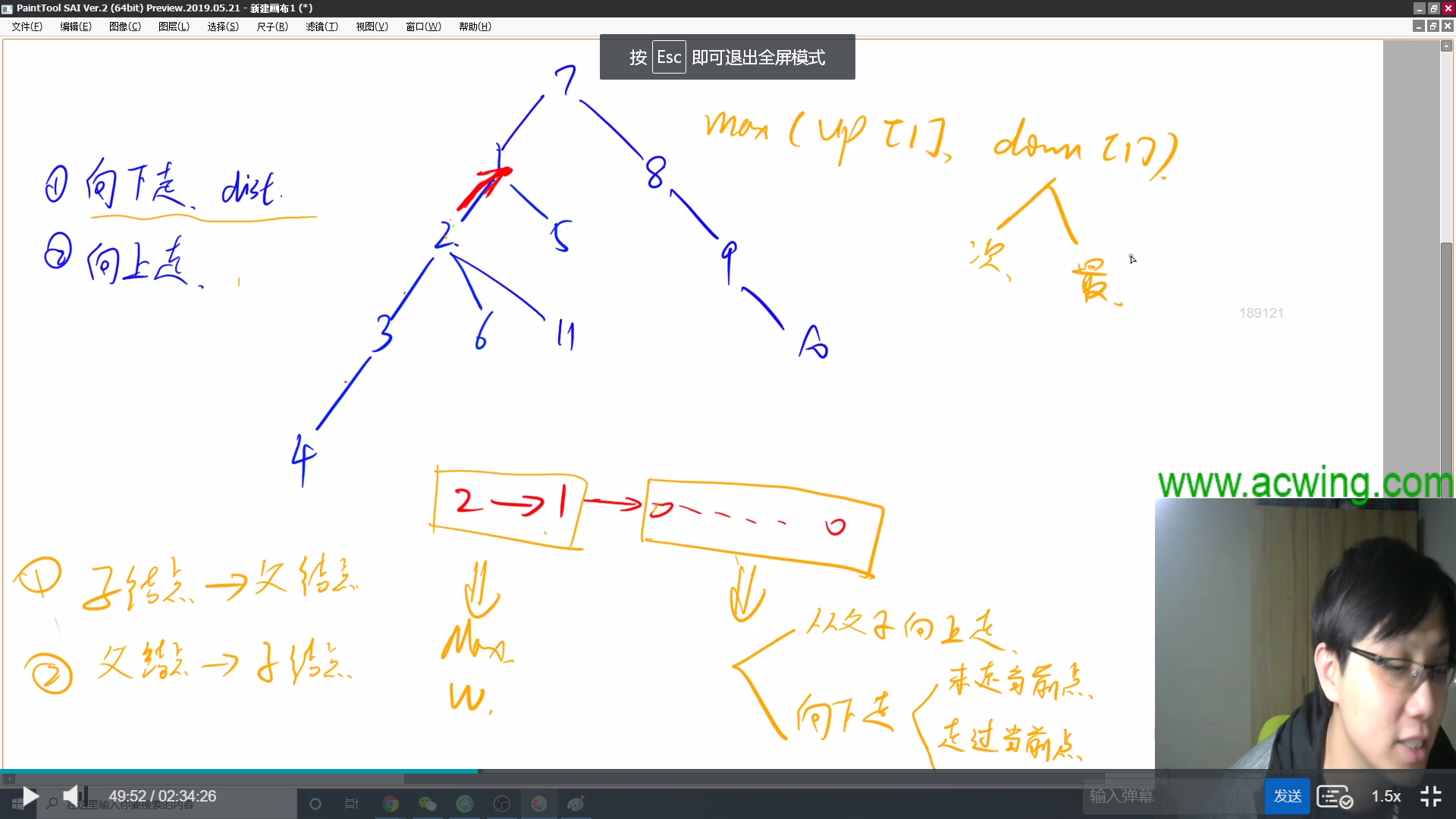
求树的中心需要，求节点到其他节点的最远距离。

最远距离分成两类：

第一类是向子节点（下）走的最远距离，

第二类是向父节点（上）走的最远距离。

可以进行两次dfs，

第一次求出向下走的最大值和次大值并记录（记录距离和节点），子->父，和求直径时dfs方法一样。

第二次则可以，更新节点向上走的最大值，父->子，

其中，当子节点向上走的最远距离为，到父节点的权重+max(父节点向上走的最远距离，父节点向下走（除了当前点）的最远距离)。

 

然后可以遍历，求出某节点到其他节点的最远距离，即为向上和向下走的最大值。